RSA: Step-by-Step

RSA: Step-by-Step
There are three amazing methods that protect you online more than virtually anything else: the Diffie Hellman (DH) method: the RSA encryption/signing method; and elliptic curve cryptography (ECC).
While elliptic curve cryptography (ECC) has generally taken over in areas of key exchange (ECDH) and in blockchain implementations (such as with ECDSA signatures), RSA is still alive and kicking in, and is still the most popular method for protecting encryption keys and in creating digital signatures.
But things are changing, and where Google, for example, uses ECC to define the public key for its YouTube.com site:

But, the intermediate signer uses RSA keys, and so the signature on the certificate is an RSA one:
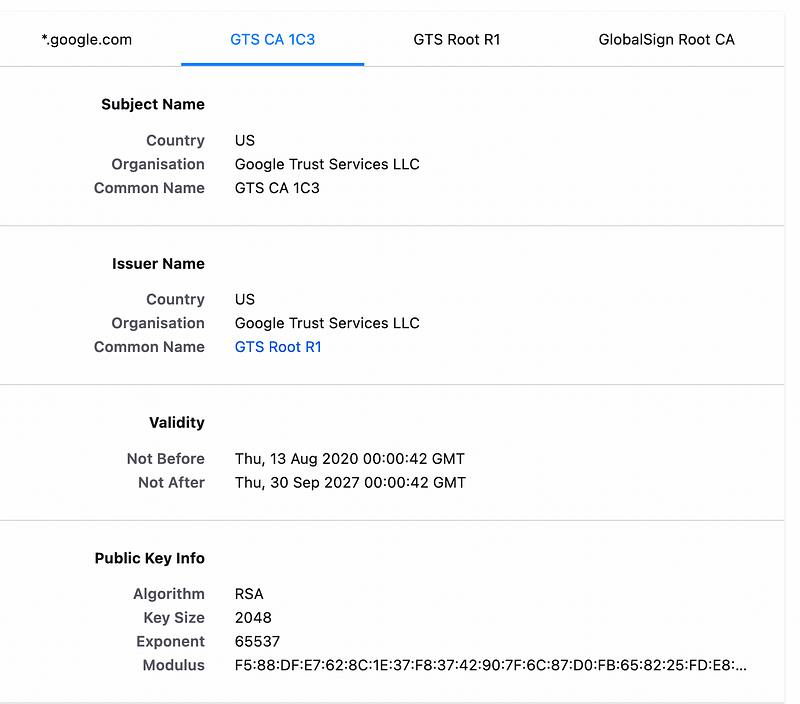
So, let’s do a step-by-step approach to RSA encryption and decryption.
Generating keys
It was Ron Rivest who used Fermat’s Little Theorem to define the operation of the RSA method. For this, we first create two random prime numbers (p and q), and then define a modulus (N):
N=p.q
We then compute PHI as:
PHI=(p-1).(q-1)
We normally then pick a public exponent of e as:
e=65,537
and then derive the private exponent of d as:
d= e^{-1} (mod N)
This is the inverse of e modulo N. Here is a method to implement this, and which uses a number of bits to define the prime numbers generated:
def genRSAKey(bits):
p = Crypto.Util.number.getPrime(bits, randfunc=Crypto.Random.get_random_bytes)
q = Crypto.Util.number.getPrime(bits, randfunc=Crypto.Random.get_random_bytes)
PHI=(p-1)*(q-1)
n=p*q
e=65537
d=pow(e,-1,PHI)
return n,e,d
The encryption process is then to take an integer value (M), and cipher it with:
C=M^e (mod N)
and then we can decrypt with:
M = C^e (mod N)
For signatures, it is the reverse, and where we take a hash of the message and compute the signature:
S = H(M)^e (mod N)
To check the signature, we use the public exponent to discover a hash of the message:
H(M) = S^e (mod N)
And, so, we need a way to convert our plain text into an integer value. For this, we convert the bytes of the message into an integer value. But we also need to fit this integer value to the same size as the module — and use random padding to make sure it fits. The module popular method is to use PKCS#1 v1.5 padding, and which takes the plaintext (P) and appends it:
WithPadding = 0x02 0x02 || random (without any zero bytes) || 0x00 || P
and in case we start with two bytes (0x0002) and then generate enough random data to make sure that WithPadding has the same number of bytes as the modulus (N). Then we have a 0x00 byte, followed by the message (P). When this is decrypted, we just need to look for the zero byte and take the message after that. In code this becomes (em):
ps = tobytes(randFunc(k-mLen-3))
em = b('\x00\x02') + ps + bchr(0x00) + message
print(f"e={e}, d={d}, N={N}")
print(f"\nModulus length: {len(em)//2} bytes or {len(em)*4} bits")
print ("With padding: ",em.hex())
print(f"\n0002 -- {ps.hex()} -- 00 --- {message.hex()}")
After this, it is easy to encrypt and decrypt:
C=pow(int.from_bytes(em, byteorder='little'),e,N)
print(f"\nCipher: {C}\n")
M_rec = pow(C,d,N)
vals =M_rec.to_bytes(k , byteorder='little')
print(f"De-cipher: {vals.hex()}\n")
The code for this is here:
https://asecuritysite.com/rsa/rsa_pkcs
Conclusions
And, that’s RSA magic! Over four decades old, and still going strong. It has secured the Internet and still does. But, ECC is coming up on the rails and might replace RSA signing. Once the intermediate and root CAs adopt ECC, we may see ECDSA signing become popular. It must be said that RSA signatures must be dealt with, with care, as the usage of PKCS#1 v1.5 can lead to a range of attacks. ECDSA signatures also need to be treated with care, especially related to nonce reuse.
If you are interested in RSA, try here:
and for ECDSA, here: