To The Builders of our Future: Meet The Chaum-Pedersen Non-Interactive Zero-Knowledge Proof Method

Using Discrete Logs and PowerShell

David Chaum (left) and Torben P Pedersen (right)

To The Builders of our Future: Meet The Chaum-Pedersen Non-Interactive Zero-Knowledge Proof Method

Using Discrete Logs and PowerShell

My knowledge has gone backwards. No, it hasn’t reversed, but I have converted my current knowledge of elliptic curves back to their roots: in discrete logarithms. And, so let’s wind the clock back to 1992, and have a look at a major breakthrough in privacy-preserving methods, and which is being scaled into our modern world. The theory is much the same, but rather than using discrete logs, we now use elliptic curve methods. In this article, I will use the might discrete logs, and implement as the paper outlined.

Before we begin, here are a couple of basic rules that we have for discrete logarithms:

An Old Data Model

We have built a data world that has little inherent respect for privacy. For this, we often pass sensitive data values that can be discovered by others. So, why can’t we have a world that just proves knowledge and not actually pass it? We could thus prove that we still know our password without actually giving away our password. This is the world of ZKP (Zero-Knowledge Proofs). The way they normally work is that Victor (the verifier) sends Peggy a challenge, and then she solves a puzzle and returns back a value that proves that she still knows her secret. But, we can convert this into a form where Peggy generates her own challenge and proof. This is known as a NI-ZKP (Non-interactive Zero Knowledge Proof).

And, so, now, let’s look at a classic method: the Chaum-Pedersen method [here]:

The Chaum-Pedersen proof

Let’s say we have two base generators (g and h), and a secret value of x. If we have g^x and h^x, how do we prove that x is the same value?

For this, we then use g, Y, h and Z within a Chaum-Pedersen proof [1] to provide a zero-knowledge proof that log_G(Y)==log_h(Z). This is defined as DLEQ(Z/M == Y/G) — discrete log equality. With this, we can prove that the same private key has been used for g^x and h^x. We make it non-interactive so that Victor does not have to challenge Peggy, but where Peggy can create her own challenge and the associated proof.

Let's say Peggy (the prover) needs to prove that two public keys use the same private key (x) but with different base points:

Peggy will generate a random value (k) and then computes two points (A and B) based on the generator points used (G and M):

With non-interactive proofs, Peggy then creates a challenge © of:

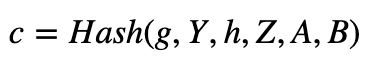
And then calculates:

and where n is the order of the curve. As a proof, Peggy then sends the following to Victor:

The verifier (Victor) then computes:

If c==c′, the proof has been proven. This works because:

Coding

The coding is fairly straightforward, apart from when the value of s or c is negative. For this, we need to perform an inverse mod operation on the value. This is done using an Extended Euclidian method:

$s=($k-$c*$x)

if ($s -lt 0) 
{ 
    $val1= ([BigInt]::ModPow($g,-$s,$p)) 
    $val2= ([BigInt]::ModPow($h,-$s,$p))
    [BigInt]$val1=Get-ExtendedEuclide $val1 $p  
    [BigInt]$val2=Get-ExtendedEuclide $val2 $p   
}
else  {
    $val1= ([BigInt]::ModPow($g,$s,$p)) 
    $val2= ([BigInt]::ModPow($h,$s,$p))
}

The full code is [here]:

$hashmethod="SHA1"

$hashmethod=$Args[0]
$bytesize=([BigInt]$Args[1])

function Get-Rand($randBytesSize) {

    $rand = [Security.Cryptography.RandomNumberGenerator]::Create()
    $r = [byte[]]::new($randBytesSize)
    $rand.GetBytes($r)
    return([System.Numerics.BigInteger]::Abs([System.Numerics.BigInteger]::new($r)))
}

# Source: https://social.technet.microsoft.com/wiki/contents/articles/33421.powershell-implementing-the-rsa-algorithm-powerrsa.aspx
function Get-ExtendedEuclide($e, $PHI) {
    $u = @(1,0,$PHI)
    $v = @(0,1,$e)               
    while ($v[2] -ne 0) {       
        $q = $u[2] / $v[2]
        $temp1 = $u[0] - $q * $v[0]
        $temp2 = $u[1] - $q * $v[1]
        $temp3 = $u[2] - $q * $v[2]
        $u[0] = $v[0]
        $u[1] = $v[1]
        $u[2] = $v[2]
        $v[0] = $temp1
        $v[1] = $temp2
        $v[2] = $temp3
    }
    if ($u[1] -lt 0) {return ($u[1] + $PHI)}
    else {return ($u[1])}
}

$x=Get-Rand 16
$g=5
$h=3
$k=Get-Rand 16
[BigInt]$p = [math]::Pow(2,255)-19

[BigInt]$Y = ([BigInt]::ModPow($g,$x,$p)) 
[BigInt]$Z = ([BigInt]::ModPow($h,$x,$p))

[BigInt]$A = ([BigInt]::ModPow($g,$k,$p)) 
[BigInt]$B = ([BigInt]::ModPow($h,$k,$p))

$cval=[string]$Y+[string]$Z+[string]$A+[string]$B
$hash1=[System.Security.Cryptography.HashAlgorithm]::Create($hashmethod).ComputeHash([System.Text.Encoding]::UTF8.GetBytes($cval))

$c=[BigInt]::new($hash1) % $p

$s=($k-$c*$x)

if ($s -lt 0) 
{ 
    $val1= ([BigInt]::ModPow($g,-$s,$p)) 
    $val2= ([BigInt]::ModPow($h,-$s,$p))
    [BigInt]$val1=Get-ExtendedEuclide $val1 $p  
    [BigInt]$val2=Get-ExtendedEuclide $val2 $p   
}
else  {
    $val1= ([BigInt]::ModPow($g,$s,$p)) 
    $val2= ([BigInt]::ModPow($h,$s,$p))
}
if ($c -lt 0) 
{ 
    $val3= ([BigInt]::ModPow($Y,-$c,$p))
    $val4= ([BigInt]::ModPow($Z,-$c,$p))
    [BigInt]$val3=Get-ExtendedEuclide $val3 $p  
    [BigInt]$val4=Get-ExtendedEuclide $val4 $p   
}
else  {
    $val3= ([BigInt]::ModPow($Y,$c,$p))
    $val4= ([BigInt]::ModPow($Z,$c,$p))
}

$A_=($val1 * $val3) % $p
$B_=($val2 * $val4) % $p

$cval=[string]$Y+[string]$Z+[string]$A_+[string]$B_
$hash1=[System.Security.Cryptography.HashAlgorithm]::Create($hashmethod).ComputeHash([System.Text.Encoding]::UTF8.GetBytes($cval))

$c_=[BigInt]::new($hash1) % $p

"== Peggy and Victor agree on some parameters =="
"g="+$g
"h="+$h
"p="+$p
"`n== Peggy generates a secret =="
"x="+$x
"`n== Peggy sends to Victor =="
"Y=g^x (mod p)"+$Y
"Z=h^x (mod p)"+$Z
"`n== To prove proof of x, Peggy generates a random value  =="
"k="+$k
"`n== To prove Peggy computes  =="
"A=g^k (mod p)="+$A
"B=h^k (mod p)="+$B
"`n== Peggy sends  =="
"c=H(Y || Z || A || B)="+$c
"s="+$s

"`n== Victor computes  =="
"A'=g^s*Y^c="+$A_
"B'=h^s*Z^c="+$B_
"c'=H(Y || Z || A' || B')="+$c_

if ($c -eq $c_) {
    "Proven"
} else {
    "Not Proven!"
}

A sample test [here]:

== Peggy and Victor agree on some parameters ==
g=5
h=3
p=57896044618658097711785492504343953926634992332820282019728792003956564819968

== Peggy generates a secret ==
x=127905488513436048082592712994569094425

== Peggy sends to Victor ==
Y=g^x (mod p)1954320240376494446293482252260132766584792497537664661414430778457018220581
Z=h^x (mod p)11108333480233328049664138958707819746749022785232553649938208591226856601251

== To prove proof of x, Peggy generates a random value  ==
k=128285104851959081500842650802536596607

== To prove Peggy computes  ==
A=g^k (mod p)=37593064446873157253774327598012471958818046706587698674433629474089101927117
B=h^k (mod p)=57037642838719057184729856693861126372590004437898505689708772465935409551531

== Peggy sends  ==
c=H(Y || Z || A || B)=-69870956537484069055136690945701471774
s=8936878828827957945079373500700037838811408036220861638164363367459414856557

== Victor computes  ==
A'=g^s*Y^c=37593064446873157253774327598012471958818046706587698674433629474089101927117
B'=h^s*Z^c=57037642838719057184729856693861126372590004437898505689708772465935409551531
c'=H(Y || Z || A' || B')=-69870956537484069055136690945701471774
Proven

Conclusions

We need to build a more private data world, and where we can prove things, and keep them private. David Chaum and Torben P Pedersen shone a bright light into the future, and which is now becoming alive. Here’s to the future!

You can play with the code here:

https://asecuritysite.com/powershell/chaum

and with elliptic curves:

https://asecuritysite.com/zero/logeq

These days, discrete log equality is being used within smart contracts, and where I can prove that I own a private key, without passing it to the smart contract.

References

[1] Chaum, David, and Torben Pryds Pedersen. “Wallet databases with observers.” Annual international cryptology conference. Springer, Berlin, Heidelberg, 1992 [paper].