ElGamal, Big Integers And PowerShell

ElGamal, Big Integers And PowerShell

We had an excellent conference this week on our campus [here]. As part of my presentation I outlined the creation of a prime number which contains a whole sequence of nines:

And for this, I used PowerShell on my Macbook. Why? Well, PowerShell is pretty good with large integer values, whereas Python can struggle with overflows, and so on. At its core is the strength of the .NET framework, and which can be ported onto most platforms (including Microsoft Windows, Mac OSX and Linux). It is also easy to port a compiled C# program into a PowerShell scripted program.

So, let’s push PowerShell a little and get it to handle the mighty ElGamal encryption method. In elliptic curves, we have integer values which can be 256 bits, whereas in discrete log methods we often use values which are greater than 1,024 bits. As our integer values in programs only go up to 64 bits, we need another way of representing our values, and that’s where Big Integers come in.

ElGamal

Initially Bob creates his public key by selecting a g value and a prime number (p) and then selecting a private key (x). He then computes Y which is:

His public key is (Y,g,p) and he will send this to Alice. Alice then creates a message (M) and selects a random value (k). She then computes a and b:

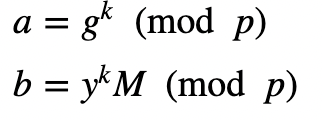
Bob then receives these (a and b), and then uses his private key (x) to decrypt the values and discover the message:

This works because:

In finite fields, the operation of 1/x (mod p) is performed as an inverse of x mod p. The first thing we need is a random number generator for our values of x and k. For this we can generate a prime number with n bits, but ranges between 0 and p-1:

function getRandom([BigInt]$p, [BigInt]$n) {
    $rngValue = [System.Security.Cryptography.RNGCryptoServiceProvider]::new()
    $bytesb = [byte[]]::new($n / 8)
    $rngValue.GetBytes($bytesb)
 $r = ([BigInt]::new($bytesb))  % $p
    if($r -le [BigInt]::Zero ) {$r = [BigInt]::Add($r, $p) } 
    return $r
}

Next we need to select a generator value (g) that will work with our prime number:

function getg([BigInt] $p){
    $One = [BigInt] 1
    $Two =  [BigInt] 2
    $etotient = [BigInt]::Subtract($p, $One)
    $g = 3
    $e = [BigInt]::Divide($etotient,$Two)

while([BigInt]::ModPow($g, $e, $p) -ne $etotient ){ 
        $g = [BigInt]::Add($g, $Two) 
    }
    return $g
}

and then finally an inverse mod function:

function inverse_mod([BigInt] $a,[BigInt] $p){ 
 # res = a^{-1} (mod p)
 $val = [BigInt]0
 $nt = [BigInt]1
 $r = $p
 $nr = $a
 while ($nr -ne [BigInt]0) {
  $q = [BigInt]::Divide($r,$nr)  
  $val_temp = $nt
  $nt = [BigInt]::Subtract($val,[BigInt]::Multiply($q,$nt))
  $val = $val_temp
  $val_temp = $nr
  $nr = [BigInt]::Subtract($r, [BigInt]::Multiply($q,$nr))
  $r = $val_temp
 }
 if ($r -gt 1) {return -1}
 if ($val -lt 0) {$val = [BigInt]::Add($val,$p)}
 return $val
}

And, that’s the basic foundation. The computation then follows the maths defined above. To generate the keys:

$p = [BigInt]::Pow(2,255)-19

$g = getg($p)
$n = 2048

$x = getRandom $p $n
"`nPrivate key: "+$x
"Prime: "+$p

$Y = [BigInt]::ModPow($g, $x, $p)
"`nPublic key (Y,p,g)=",$Y, $p, $g

To encrypt:

$k=getRandom $p  $n

$a = [BigInt]::ModPow($g, $k, $p)
$s = [BigInt]::ModPow($Y, $k, $p)

$b = ([BigInt]::Multiply($message, $s)) % $p
"`nCiphers:\n"
"`na="+$a
"`nb="+$b

and then to decrypt:

$aval = [BigInt]::ModPow($a, $x, $p)
$aval_inv = inverse_mod $aval $p
$decrypt = ([BigInt]::Multiply($aval_inv, $b)) % $p

"`nDecrypted: "+$decrypt

The whole program is here:

https://asecuritysite.com/powershell/elgamal_ps

and a sample run is:

Message (m)=444

Private key: 9106828700547370271854754434087843280227915454206249744665473871172819179168
Prime: 57896044618658097711785492504343953926634992332820282019728792003956564819949

Public key (Y,p,g)=
45843051653271161916620984136646627066048538575035508681301086730979897188044
57896044618658097711785492504343953926634992332820282019728792003956564819949
7

Ciphers:\n

a=8680995481259943884053499833431759100943185361122621303552498628614856645551

b=29531620544981006726766089814864107165718029562949828484679701389083988643146

Decrypted: 444

Conclusions

ElGamal encryption has special properties that are useful in the modern age. One is that we can apply partial homomorphic encryption. If you are interested in learning more, try here:

https://asecuritysite.com/elgamal/

These days, we normally use ElGamal encryption with elliptic curves, the core theory still applies through discrete log methods.