Homomorphic Multiplication and Division Using ElGamal in PowerShell

Data exists in three main states: over-air, at-rest and in-process. While we have encryption for over-air (such as with TLS and wireless…
Photo by Marija Zaric on Unsplash

Homomorphic Multiplication and Division Using ElGamal in PowerShell

Data exists in three main states: over-air, at-rest and in-process. While we have encryption for over-air (such as with TLS and wireless encryption) and for at-rest (such as for disk encryption), we often do not protect our data within process. And, so, if someone gets access to the memory they would reveal sensitive information such as passwords and encryption keys.

Homomorphic encryption aims to overcome this problem, and where we can process data using encrypted values. This involves generating a private key and a public key, and where we encrypt the data with the public key, and then can process the values using arithmetic values, and then decrypt the result with the private key. Overall, we can have partial homomorphic encryption (PHE) or full homomorphic encryption (FHE). We can also have methods which operate just on integers, and others that deal with floating point values.

While new methods, such as CKKS (Cheon, Kim, Kim and Song) are defined for FHE, there is a performance hit for the processing. If we just need to multiply or divide integers, then some of our existing public key methods can be used, and where they typically have good performance levels against the FHE methods. One of these is the usage of ElGamal encryption, and which naturally supports multiplication and division. So let’s implement these in PowerShell.

ElGamal

In its purest form, ElGamal encryption uses discrete logs but is now often used with elliptic curves. Initially, Bob creates his public key by selecting a g value and a prime number (p) and then selecting a private key (x). He then computes Y which is:

His public key is (Y,g,p) and he will send this to Alice. Alice then creates a message (M) and selects a random value (k). She then computes a and b:

Bob then receives these (a and b), and then uses his private key (x) to decrypt the values and discover the message:

This works because:

In finite fields, the operation of 1/x (mod p) is performed as an inverse of x mod p. A demonstration of encryption and decryption is here:

https://asecuritysite.com/powershell/elgamal_ps

Homomorphic multiplication

To multiply homomorphically, we have:

Then we get:

The code to encrypt, decrypt and multiply is:

function encrypt($g, $p, $n, $message) {
    $k=getRandom $p  $n

    $a = [BigInt]::ModPow($g, $k, $p)
    $s = [BigInt]::ModPow($Y, $k, $p)
    $b = ([BigInt]::Multiply($message, $s)) % $p
    return $a,$b
}

function decrypt($a, $b, $x, $p) {

    $aval = [BigInt]::ModPow($a, $x, $p)
    $aval_inv = inverse_mod $aval $p
    $d = ([BigInt]::Multiply($aval_inv, $b)) % $p
    return $d
}

function homomorphic_multiply($a1, $b1, $a2, $b2) {
    $a=$a1*$a2
    $b=$b1*$b2
    return ($a,$b)
}

The full code is here:

https://asecuritysite.com/powershell/elgamal_ps2

and a sample run for 123 multiplied by 2 is [here]:

Val 1: 123
Val 2: 2
Private key: 8110526336833461392694766893144765884975539500638608369614246491065989597104
Prime: 57896044618658097711785492504343953926634992332820282019728792003956564819949
Public key (Y,p,g)=
38236323508027086188597506954417918017240973568749764937934483935657361297791
57896044618658097711785492504343953926634992332820282019728792003956564819949
7
Ciphers:
a1=51761118376267175467107421570092662695854197334527456646530169127880244225119
b1=29850910616342830825910227672366973843425133260771328183701882195028806956100
a2=30530473459232922567476752842348735909115755475726954456809815701366518625232
b2=20675127244510533152445504514001125638454187657393668446997689262768125152571
a=37220264461004882521190997342023275740924605322509879123967474082694960700431
b=23795419255293351804429745378282706642929644124508519949664462974887141454749
Decrypted: 246
Decrypted: 61

Homomorphic division

For division, we take the inverse of the divisor (a2, b2) values:

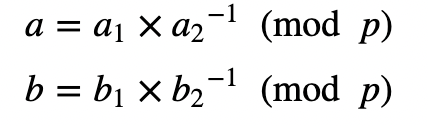
This is implemented as an inverse mod p operation

function homomorphic_divide($a1, $b1, $a2, $b2, $p) {
    $aval2_inv = inverse_mod $a2 $p
    $bval2_inv = inverse_mod $b2 $p
    $a=($a1*$aval2_inv) % $p
    $b=($b1*$bval2_inv) % $p
    return ($a,$b)
}

The full code for this is here:

https://asecuritysite.com/powershell/elgamal_ps3

and a sample run is:

Val 1: 122
Val 2: 2
Private key: 22176049143396515587044301005691117544848995522078536165826426281069072894575
Prime: 57896044618658097711785492504343953926634992332820282019728792003956564819949
Public key (Y,p,g)=
22560767275166360029397209269945844019446153193399210722052535370444773715959
57896044618658097711785492504343953926634992332820282019728792003956564819949
7
Ciphers:
a1=10080586196483418290226984021269503030094467967262647094190748916217599207040
b1=43319315414913305644803164872098427805273438670310837877616397667911849695388
a2=28786341111040935175680087270292908520183304213353992744849803491634173275824
b2=210139691869864165919442793913722534472649700534993734395323924538494631450
a=4179869465056057121768003536717792919542153753511598961905128857022424138720
b=11507278436299506119405044288241948789553429760515588688169141826714165957807
Decrypted: 61

Conclusion

The pure ElGamal method is hardly used in encryption at the current time, but it was used to create the DSA (Digital Signature Algorithm) signature method, and which has now become ECDSA (Elliptic Curve Digital Signature Algorithm). But, now is the time for ElGamal to make a return, and which allows us to perform multiplies and divides in a private-preserving way.

If you are interested in the ElGamal method, try here:

https://asecuritysite.com/elgamal

and for PowerShell:

https://asecuritysite.com/powershell/

It should be noted, that for performance reasons, the prime number I have used is relatively small and well-known. In real life, we would use a prime number that had at least 1,024 bits, and that was randomly generated.

References

[1] Cheon, J. H., Kim, A., Kim, M., & Song, Y. (2017, December). Homomorphic encryption for arithmetic of approximate numbers. In International conference on the theory and application of cryptology and information security (pp. 409–437). Springer, Cham.