Your Online Security is Fundamentally Dependent on Hard Problems …

Your Online Security is Fundamentally Dependent on Hard Problems …

Primitive root of a prime number p modulo p in PowerShell

Our online security is fundamentally dependent on hard problems. Unfortunately, most of the methods used cannot be proven to be hard problems, and where the RSA method, discrete logs and elliptic curve methods will generally not be hard problems in a post-quantum computer world. But, for just now:

is generally a hard problem to find x, if we know Y, g and p (as long the prime number — p - is large enough). These days, p needs to have at least 1,024 bits to be secure, and in many cases much more than that. But, can we pick any value of g and p? Well, normally we randomly generate a number of a given size, and then increment the value until we find that it is a prime number. Next, we must find a value of the generator g, that will work with this prime number.

So, if we have g^x (mod p) and where p is a prime number, can we find a value of g that makes sure that we get a unique output from 1 to p−1, for every value of x from 0 to p−2? This is known as the primitive root under modulo p.

First, we need the Euler Totient Function (Φ) and which is:

Φ=p−1

Next, we find all the prime factors of Φ. All powers are then computed as phi divided by each prime factor. After this, all the powers from i=2 to p−1 are tested for:

If this is 1, then i is not a primitive root of p. If it is never 1, we return i. The follwoing is then the basic method using PowerShell. It should be noted we are using Big Integers for the values:

function getg([BigInt] $p){
    $One = [BigInt] 1
    $Two =  [BigInt] 2
    $etotient = [BigInt]::Subtract($p, $One)
    $g = 3
    $e = [BigInt]::Divide($etotient,$Two)

    while([BigInt]::ModPow($g, $e, $p) -ne $etotient ){ 
        $g = [BigInt]::Add($g, $Two) 
    }
    return $g
}

The basic form is:

where we have a generator value (g) and a prime number p. If select a prime number of 7, and then select g values of 2, 3, 4 … 9, and then calculate the results we get:

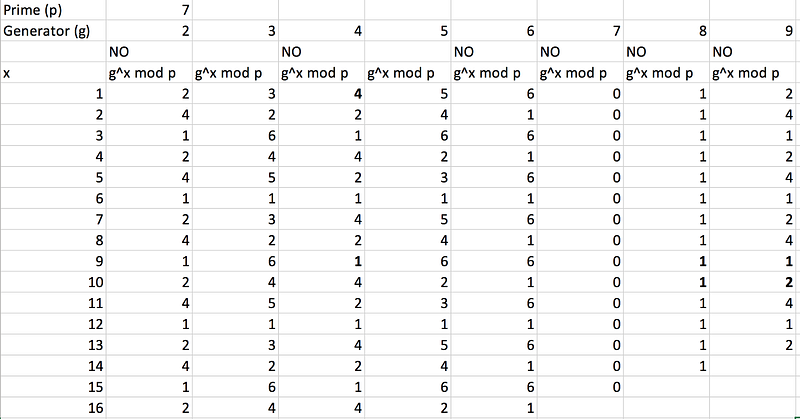
Now, look at g=2, we get an output of 2, 4, 1, 2, 4 … for the sequence values of 1, 2, … This means that we do not get a unique output for the values from 1 to 6 (where the maximum value will be six as we take the modulus of 7). But look at g=3, we get 3 (3^1(mod7)), 2 (3^2(mod7)), 6 (3^3(mod7)), 4 (3^4(mod7)), 5 (3^5(mod7)), and 1 (3^6(mod7)), which means that we get a unique value for all the possible outputs from 1 to 6, and which then repeats. For a prime number of 7, the valid values of g are 3 and 5.

The Powershell coding is:

function getg([BigInt] $p){
    $One = [BigInt] 1
    $Two =  [BigInt] 2
    $etotient = [BigInt]::Subtract($p, $One)
    $g = 3
    $e = [BigInt]::Divide($etotient,$Two)

    while([BigInt]::ModPow($g, $e, $p) -ne $etotient ){ 
        $g = [BigInt]::Add($g, $Two) 
    }
    return $g
}

$prime = [BigInt]::Pow(2,255)-19

try {
    if ($Args.Count -gt 0) {
     $prime=[BigInt]::new($Args[0]) 
    }
} catch {
    "Value needs to be an integer"
    }

"`nPrime: "+$prime

$g = getg $prime

"`ng="+$g

A sample run for p=997 is:

Prime: 997

g=5

And where we could use g=5 for the generator, but not g=3.

Conclusions

While discrete logs have made way for elliptic curve methods, they are still fundamental in defining the methods that we use.