He Basically Secured The Internet: Peter Montgomery, RIP

He Basically Secured The Internet: Peter Montgomery, RIP

Much of the core security of our current world is built on the amazing work done by individuals in the 1980s. It is to Ron Rivest (including RSA, digital signatures, and MD5), Adi Shamir (including RSA, Shamir Sharing, Cryptoanalysis, and Zero-Knowledge Proofs), Whitfield Diffie (the Diffie-Hellman method), Ralph Merkle (Merkle Trees) and many others, that we turn to for our core security.

At the forefront of this was Peter Montgomery and who died on 18 Feb 2020. Peter was previously a researcher in Microsoft Research, and in his amazing career he created Montgomery multiplication, Montgomery elliptic curves, and the Montgomery ladder. Here is one of his classic papers [here]:

One of Peter’s great contributions, too, is the Montgomery Ladder [here][1]:

The core of security on the Internet …

The core of the security on the Web comes down to … elliptic curve cryptography (ECC). With the ECDH (Elliptic Curve Diffie Hellman) handshake method, we have an almost perfect way to generate a shared key between Bob and Alice, without Eve ever finding it out. And so we turn to Curve 25519, and which is one of the best elliptic curves around. It uses the Montgomery curve form of:

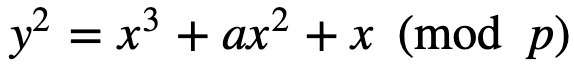
And where we take a base point (G), and then create a private key (n), and then determine our public key (nG). With this nG is the point G added n times (G+G+…G). Curve 25519 was created by Daniel J Bernstein, and who has contributed so much to cybersecurity. The form he chose was:

and where p=²²⁵⁵-19. It thus gave 128-bit security levels, and which is currently strong enough in most applications. The base point chosen is x=9, and which gives a point of:

P=( 9 , 14781619447589544791020593568409986887264606134616475288964881837755586237401 )

The point adding and scaling uses the method defined in RFC 7748 [here]:

Montgomery Multiplication

Our world of public key cryptographic is build within finite fields. We take a prime number N, and then all our operations are done with (mod N). The basic security of our systems are then determine by the number of bits in N. If N has 1,024 bits or more, we are normally fairly secure. Many of our operations are then done with multiplication or with exponential, such as:

C = Mᵉ (mod N)

or with:

Cipher = ab (mod N)

In our labs I see quite a quite few students then doing this:

Cipher = (M**e % N)

And while it will work with relatively small values, it will never work in production, as the calculation of M^e will take a long time. For example, let’s take an e value of 65,637 (the most common value for e in RSA is 65,537), and M as 11, and see the size of the number we produce:

And so if we do M^e and then (mod N) it is going to be rather inefficient.

With the RSA and the Diffie-Hellman method we perform large exponential calculations, such as:

C = Mᵉ (mod N)

and where we will continually multiply large integers by an exponent to get a result. If we were to just calculate x^y and then take (mod N) it would take a while to produce the result (possibly minutes for large numbers). Thus we use Montgomery modular multiplication, and which significantly reduces the time to compute the result. In a traditional multiplication of two value (x and y) for a modulus of N, we multiply x times y and then divide by N to find the remainder. The number of bits in the multiplication with this be the number of bits in x added to the number of bits in y. In Montgomery reduction we add multiples of N in order to simplify the multiplication.

An example of this is here, and a sample run for x=10, y=5 and N=29 is [here]:

a=10, b=5, p=29
Result: 10*5 (mod 29) = 21
Traditional method result = 21
Result: 10^5 (mod 29) = 8
Traditional method result = 8

In this case we get 50 (mod 29) which is 21, and 105 (mod 29) which is 8.

The sample code is [here]:

ackage main
 
import (
    "fmt"
    "math/big"
    "os"
    "strconv"
)
 
// == From https://rosettacode.org/wiki/Montgomery_reduction#Go
type mont struct {
    n  uint     // m.BitLen()
    m  *big.Int // modulus, must be odd
    r2 *big.Int // (1<<2n) mod m
}

func newMont(m *big.Int) *mont {
    if m.Bit(0) != 1 {
        return nil
    }
    n := uint(m.BitLen())
    x := big.NewInt(1)
    x.Sub(x.Lsh(x, n), m)
    return &mont{n, new(big.Int).Set(m), x.Mod(x.Mul(x, x), m)}
}
 

func (m mont) reduce(t *big.Int) *big.Int {
    a := new(big.Int).Set(t)
    for i := uint(0); i < m.n; i++ {
        if a.Bit(0) == 1 {
            a.Add(a, m.m)
        }
        a.Rsh(a, 1)
    }
    if a.Cmp(m.m) >= 0 {
        a.Sub(a, m.m)
    }
    return a
}
// ==

func main() {

    p:=13
    a:=5
    b:=6

    argCount := len(os.Args[1:])

    if (argCount>0) {a,_= strconv.Atoi(os.Args[1])}
    if (argCount>1) {b,_= strconv.Atoi(os.Args[2])}
    if (argCount>2) {p,_= strconv.Atoi(os.Args[3])}

    m  := big.NewInt(int64(p))

    fmt.Printf("a=%d, b=%d, p=%d\n\n",a,b,p)
 
    mr := newMont(m)
 
    x1 := big.NewInt(int64(a))
    x2 := big.NewInt(int64(b))
  
    t1 := mr.reduce(new(big.Int).Mul(x1, mr.r2))
    t2 := mr.reduce(new(big.Int).Mul(x2, mr.r2))

    res := mr.reduce(new(big.Int).Mul(t1, t2))

    fmt.Printf("Result: %s*%s (mod %s) = %s\n",x1,x2,m,mr.reduce(res)) 

    mul:=new(big.Int).Mul(x1, x2)
    fmt.Printf("Traditional method result = %s\n\n",mul.Mod(mul,m))


    prod := mr.reduce(mr.r2)              
    base := mr.reduce(new(big.Int).Mul(x1, mr.r2))

    exp := new(big.Int).Set(x2)          
    for exp.BitLen() > 0 {
        if exp.Bit(0) == 1 {
            prod = mr.reduce(prod.Mul(prod, base))
        }
        exp.Rsh(exp, 1)
        base = mr.reduce(base.Mul(base, base))
    }

    fmt.Printf("\nResult: %s^%s (mod %s) = %s\n",x1,x2,m,mr.reduce(prod)) 

    fmt.Printf("Traditional method result = %s",new(big.Int).Exp(x1, x2, m))
    
}

Peter Montgomery created the Montgomery ladder [1], and which computes a point multiplication (kG) within a fixed amount of time. This means that it is immune from timing and power attacks. The method uses a double-and-add approach apart from where it uses the same number of point additions and doubles regardless of the value of k. Basically, to determine kP, we use the representation of:

where:

The core algorithm is [here]:

R0 <- 0
R1 <- P
for i from m downto 0 do
    if ki = 0 then
        R1 <- point_add(R0, R1)
        R0 <- point_double(R0)
    else
        R0 <- point_add(R0, R1)
        R1 <- point_double(R1)
    return R0

Conclusions

We have said farewell to Peter, but he has left a lasting legacy on this world, and it is a much more secure world due to his methods.

References

[1] Montgomery, Peter L. (1987). “Speeding the Pollard and elliptic curve methods of factorization”. Math. Comp. 48 (177): 243–264. doi:10.2307/2007888.