Towards A More Private Data World — Adding and Subtraction with Homomorphic Encryption

Towards A More Private Data World — Adding and Subtraction with Homomorphic Encryption
Meet Pascal
In 1999, as part of his PhD, Pascal Paillier created a wonderful public key encryption method that allows us to add, subtract and scalar multiply encrypted values [1]:

It was a slow-burner of a paper that took a while to take hold:


But, now, in a world which is starting to respect the privacy of data, we see it making its full impact, with 573 citations in 2022. Why the impact now? Well, many of the methods proposed for homomorphic encryption are based on lattice methods, but they tend to have heavy requirements for processing. And, so, Paillier encryption is much more efficient, and can easily process addition, subtraction, and scalar multiplication. In machine learning, for example, there are many operations that are just additions and subtractions, so it is well matched to the requirements for privacy-preserving machine learning.
The Paillier method
The Paillier cryptosystem is thus a partial homomorphic encryption (PHE) method, and here two encrypted values can be added together, and the decryption of the result gives the addition [1]. If we take two values: m_1 and m_2, we get two encrypted values of Enc(m_1) and Enc(m_2). We can then multiply the two cipher values to get Enc(m1+m2). We can then decrypt to get m_1+m_2. Along with this, we can also subtract to Enc(m_1−m_2). This is achieved by taking the inverse modulus of Enc(m2) and multiplying it with Enc(m_1). Finally, we can perform a scalar multiply to get Enc(m_1⋅m_2) and which is generated from Enc(m_1)m_2.
Creating key pair
First, we select two large prime numbers (p and q) and compute:

and where lcm is the least common multiple. We then select random integer g for:

We must make sure that n divides the order of g by checking the following:

and where L is defined as L(x)=x−1N. The public key is (N,g) and the private key is (λ,μ). This can be coded as:
def keygen(bits):
p = random_prime(2^bits)
q = random_prime(2^bits)
Lambda = (p - 1) * (q - 1)
n = p * q
Zn = IntegerModRing(n)
Zn2 = IntegerModRing(n^2)
g = Zn2(n + 1)
mu = Zn(Lambda)^-1
return ((n, g), (Lambda, mu))Encrypting data
To encrypt a message (M), we select a random r value and compute the ciphertext of:

This can be coded as:
def encrypt(m, pub):
(n, g) = pub
Zn2 = IntegerModRing(n^2)
r = Zn2(randint(0, n))
c = g^m * r^n
return cDecrypting data
We can then decrypt with:
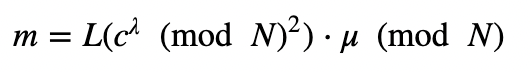
This can be coded with:
def decrypt(c, priv):
((n, g), (Lambda, mu)) = priv
Zn = IntegerModRing(n)
c = Zn((Integer(c^Lambda) - 1) / n) * mu
return cAdding and scalar multiply
If we take two ciphers (C1 and C2), we get:
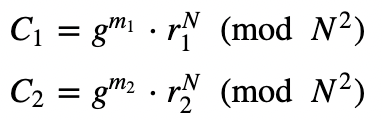
If we now multiply them we get:

And so adding two values requires a multiplication of the ciphers. This can be coded as:
def encrypt_add(cipher_1, cipher_2, pub):
(n, g) = pub
Zn2 = IntegerModRing(n^2)
r = Zn2(randint(0, n))
return cipher_1 * cipher_2 * r^nSubtraction
For subtraction of cipher1 and cipher2, we basically find the inverse mod of cipher2, and then just multiply the values (cipher1×cipher2^{-1}). The coding of this is then:
def encrypt_sub(cipher_1, cipher_2, pub):
(n, g) = pub
Zn2 = IntegerModRing(n^2)
r = Zn2(randint(0, n))
inv_cipher_2 =Zn2(cipher_2)^-1
return cipher_1 * inv_cipher_2 * r^nCoding
The final Sage coding is [here]:
def keygen(bits):
p = random_prime(2^bits)
q = random_prime(2^bits)
Lambda = (p - 1) * (q - 1)
n = p * q
Zn = IntegerModRing(n)
Zn2 = IntegerModRing(n^2)
g = Zn2(n + 1)
mu = Zn(Lambda)^-1
return ((n, g), (Lambda, mu))
def encrypt(m, pub):
(n, g) = pub
Zn2 = IntegerModRing(n^2)
r = Zn2(randint(0, n))
c = g^m * r^n
return c
def decrypt(c, priv):
((n, g), (Lambda, mu)) = priv
Zn = IntegerModRing(n)
c = Zn((Integer(c^Lambda) - 1) / n) * mu
return c
def encrypt_add(cipher_1, cipher_2, pub):
(n, g) = pub
Zn2 = IntegerModRing(n^2)
r = Zn2(randint(0, n))
return cipher_1 * cipher_2 * r^n
def encrypt_sub(cipher_1, cipher_2, pub):
(n, g) = pub
Zn2 = IntegerModRing(n^2)
r = Zn2(randint(0, n))
inv_cipher_2 =Zn2(cipher_2)^-1
return cipher_1 * inv_cipher_2 * r^n
def encrypt_scalar_mul(a, c, pub):
return c^a;
def encrypt_linear(a, cipher_1, b, cipher_2, pub):
(n, g) = pub
Zn2 = IntegerModRing(n^2)
r = Zn2(randint(0, n))
return (cipher_1^a) * (cipher_2^b) * r^n
priv = keygen(512)
pub = priv[0]
message_1 = randint(0, 1000)
cipher_1 = encrypt(message_1, pub)
message_2 = randint(0, 1000)
cipher_2 = encrypt(message_2, pub)
sum = encrypt_add(cipher_1, cipher_2, pub)
diff =encrypt_sub(cipher_1, cipher_2, pub)
ret = encrypt_linear(5, cipher_1, 4, cipher_2, pub)
print (f"Public key (n,g): {priv[0]}")
print (f"Private (Lambda, mu): {priv[1]}")
print ("Message 1 = %d" %message_1)
print ("Cipher 1 = %d" %cipher_1)
print ("Message 2 = ", message_2)
print ("Cipher 2 = ", cipher_2)
print ("Message addition = ", message_1 + message_2)
print ("Message addition (after decrypt) = ", decrypt(sum, priv))
print ("Message substraction = ", message_1 - message_2)
print ("Message substraction (after decrypt) = ", decrypt(diff, priv))
print ("5 * message_1 + 4 * message_2 = ", 5*message_1 + 4*message_2)
print ("5 * message_1 + 4 * message_2 = ", decrypt(ret, priv))A sample run with 512-bit random primes is [here]:
Public key (n,g): (23156947669113824885028372677403165457181953388059865789456104316817515040014659654816138648966119088603312471626651499885548608541051148514310897661003677407209828414138772401948058214284430464014681644682916952832047854580932609033968855525871794923711975174885943983349721211191319285535334495960825909369, 23156947669113824885028372677403165457181953388059865789456104316817515040014659654816138648966119088603312471626651499885548608541051148514310897661003677407209828414138772401948058214284430464014681644682916952832047854580932609033968855525871794923711975174885943983349721211191319285535334495960825909370)
Private (Lambda, mu): (23156947669113824885028372677403165457181953388059865789456104316817515040014659654816138648966119088603312471626651499885548608541051148514310897661003663160352333484425625515225987525084761636803628875574761376993786918482547687400189721495111542857144782001887515329993646495134121685461868580940124487796, 1134370614907233721198964121818613931852083753296294721882623172107576528430891563435660499764437730695221416907143831604938922901228289321593896490122692893030268487819732858525254005758498978253634382117438121603758494079513558906280922665379550486373823399245016232464214516723654187691659750027715864323)
Message 1 = 358
Cipher 1 = 281891348698992329573398004777173134921526193816021265628226274250891957055727285746116412762257363632972424427647801724565593449191445103240458122016958242562955932411850935748128613170879432188553611429053847382979227317702212662825112505136559223801337675396624623709509405354236007738301527433685289946832406969478342982688150732180217936775580972378203884630576168757832631409958697663216190861233887271341646720634910541676133593491085918988439670721045775284305606202305632898230130293279352732554554855348076455691598665977263087275958845918515266601987112296746156592206218319572783888449184132594971586040
Message 2 = 826
Cipher 2 = 180968880445559996973328604485836263236854646724372993576681733394033475721273332316550875891209801738195416657393773900167230357593451051407824260007575725942648201371312184307821954858269464587737034414021158574963418335452923613403491947371288734063440998185064853033386520126317837484721115438739713967002821026961631364141972415581139304377838513486380415766480810432027922149838366877449375428549724873388958162330923932636038678062209953565356699740742714962654774530856531813826544230271917773382769169800535292601562152429050509281870562249034364854300377678178581575564020187632537687005425384190105523291
Message addition = 1184
Message addition (after decrypt) = 1184
5 * message_1 + 4 * message_2 = 5094
5 * message_1 + 4 * message_2 = 5094and [here]:
Public key (n,g): (44368249461374736221518975811396221973756996299852989777834990193266262268370854148615764822789641884266520226976073301904253157901064611191854974040896083338730134914940616723469953570285030543099156065869322238541478677311999538306831763329712608359081709861432634653352649567137710953082774795055303895279, 44368249461374736221518975811396221973756996299852989777834990193266262268370854148615764822789641884266520226976073301904253157901064611191854974040896083338730134914940616723469953570285030543099156065869322238541478677311999538306831763329712608359081709861432634653352649567137710953082774795055303895280)
Private (Lambda, mu): (44368249461374736221518975811396221973756996299852989777834990193266262268370854148615764822789641884266520226976073301904253157901064611191854974040896068471475172171442422122065326592894586119896839615552025968584660743277131293410153120208038066656398291303766909587710219933404632887417697564068149967120, 12998809018843064146792386977888024526547135469695110908738440867634560951272261235213160245291238462479403432949466995726092080256965739640023741026308193474620001309448701325574267198861808340644365435644360393168339654047181283031694817595586728791725014177047105648308494660402325484883095459374529101931)
Message 1 = 737
Cipher 1 = 657218563629840011477815607385732859875210452407239126369294426702323474911771250618699709835083663406351338295880688962791349390477510941195128134529608166713006898310714202162799966165831936086715944083797918160486088586356187859251723857920502452279802495883736467640761475323782045655451289183983371966708340511602453837178320054109403551872136462702365511307403119684686441415313718651716491611227182120803176499987288298135113069795659739084794752950693738466850794198331246203792984529369770173306604732392276019071110599506394491464128687341767214105123703592717302900725990226522164509797426485942186503900
Message 2 = 59
Cipher 2 = 624335194021488801113717789766732979501082924839791663578791902511770746400450805388937028840457605923278634274974823140501956644347255922146603629750511813218393046168739670301115580197056031495837169171950226877504012473397686500847125443176325305856602702889333297857509991135334688297955409052969027363657074780846326288479747939637836326615074356858975309644138789521258939264590326527335622280042065400601616924861479063709960496266525292419951862004111370126986036945044907808368996542604575173713417774440153478227455610820325393836377745539109745781900938744373328251487785529304479310809853281533939954992
Message addition = 796
Message addition (after decrypt) = 796
5 * message_1 + 4 * message_2 = 3921
5 * message_1 + 4 * message_2 = 3921Conclusions
Now is the time to finally close the door on protecting data in memory and in process. For the first time, we now have the methods and the computing power to implement systems that respect privacy. If you want to find out more about the Paillier method, try here:
https://asecuritysite.com/paillier
and here:
References
[1] Paillier, P. (1999, May). Public-key cryptosystems based on composite degree residuosity classes. In International conference on the theory and applications of cryptographic techniques (pp. 223–238). Springer, Berlin, Heidelberg [here].