Not How The Grinch Stole Christmas, But How Galois Saved Cybersecurity

Not How The Grinch Stole Christmas, But How Galois Saved Cybersecurity
So, for an electrical engineer, the most fundamental knowledge that every practicing engineer has is Ohm’s Law. But, what’s the most basic knowledge that a cryptographer should know? Well, I think it is the magic of Galois fields, and which has saved our cybersecurity world, and will scale into a future of lattice-based cryptography. These lattice methods are based on polynomial operations and Galois fields and will replace our existing public key methods of RSA, ECC and discrete logs.
Okay. So here’s my Christmas essay, and it’s not about how the Gringe Stole Christmas, but about how Galois saved cybersecurity. The Galois in this case is Évariste Galois, and who invented Galois fields. He lived from 1811 to 1832, and where his short life was ended from the wounds he received in a duel.
Z_p (mod p)
First, let’s start with the problem. In finite fields, we have a (mod n) operation for a list of integers (Z), and where n is a prime number. This works for our add (+) and multiply (*) operations, and where:
a (mod n) + b (mod n) = (a+b) (mod n)
a (mod n) *b (mod n) = (a*b) (mod n)
If we take Z_7, we get [here]:
Additive group for Z_7
+ | 0 1 2 3 4 5 6
-----------------
0 | 0 1 2 3 4 5 6
1 | 1 2 3 4 5 6 0
2 | 2 3 4 5 6 0 1
3 | 3 4 5 6 0 1 2
4 | 4 5 6 0 1 2 3
5 | 5 6 0 1 2 3 4
6 | 6 0 1 2 3 4 5
Multiplicative group for Z_7
+ | 0 1 2 3 4 5 6
-----------------
0 | 0 0 0 0 0 0 0
1 | 0 1 2 3 4 5 6
2 | 0 2 4 6 1 3 5
3 | 0 3 6 2 5 1 4
4 | 0 4 1 5 2 6 3
5 | 0 5 3 1 6 4 2
6 | 0 6 5 4 3 2 1 We can see that for the additive group, for every permutation, we end up with a different value within the group, and where:
4+0 (mod 7) = 4; 4+1 (mod 7) = 5; 4+2 (mod 7) = 6; 4+3 (mod 7) = 0; 4+4 (mod 7) = 1; and so on.
For multiplicative, we also get all the possible values in the group:
4*0 (mod 7) = 0; 4*1 (mod 7) = 4; 4*2 (mod 7) = 1; 4*3 (mod 7) = 5; and so on.
For the -a (the inverse addition), we look up the table until we find a zero value as a result. Again, these correspond to all the possible outputs. For the invere multiplication (a^{-1}) we look up the values which result in 1, and get the inverse multiply of 2 is 4, and the inverse multiply of 3 is 5.
But now let’s test for a non-prime number, such as n=8 [here]:
Additive group for Z_8
+ | 0 1 2 3 4 5 6 7
-------
0 | 0 1 2 3 4 5 6 7
1 | 1 2 3 4 5 6 7 0
2 | 2 3 4 5 6 7 0 1
3 | 3 4 5 6 7 0 1 2
4 | 4 5 6 7 0 1 2 3
5 | 5 6 7 0 1 2 3 4
6 | 6 7 0 1 2 3 4 5
7 | 7 0 1 2 3 4 5 6
Multiplicative group for Z_8
+ | 0 1 2 3 4 5 6 7
-------
0 | 0 0 0 0 0 0 0 0
1 | 0 1 2 3 4 5 6 7
2 | 0 2 4 6 0 2 4 6
3 | 0 3 6 1 4 7 2 5
4 | 0 4 0 4 0 4 0 4
5 | 0 5 2 7 4 1 6 3
6 | 0 6 4 2 0 6 4 2
7 | 0 7 6 5 4 3 2 1Now, the additive group is fine, but the multiplicative group does not cycle through all the possible outputs. We see that for a=4 we get:
+ | 0 1 2 3 4 5 6 7
--------------------
4 | 0 4 0 4 0 4 0 4Thus 1*4 (mod 8) gives 4, and also 4*3 (mod 8) gives 4. This would cause us problems with our cryptography operations, two operations can give the same result. The program to implement this is [here]:
import sys
n=8
if (len(sys.argv)>1):
n=int(sys.argv[1])
print(f"Additive group for Z_{n}")
print ("+ | ",end="")
for i in range(0,n): print(i,end=" ")
print ("\n-------")
for i in range(0,n):
print (i,end=" | ")
for j in range(0,n):
print((i+j)%n,end=" ")
print()
print(f"\nMultiplicative group for Z_{n}")
print ("* | ",end="")
for i in range(0,n): print(i,end=" ")
print ("\n-------")
for i in range(0,n):
print (i,end=" | ")
for j in range(0,n):
print((i*j)%n,end=" ")
print()
import sys
n=8
if (len(sys.argv)>1):
n=int(sys.argv[1])
print(f"Additive group for Z_{n}")
print ("+ | ",end="")
for i in range(0,n): print(i,end=" ")
print ("\n-------")
for i in range(0,n):
print (i,end=" | ")
for j in range(0,n):
print((i+j)%n,end=" ")
print()
print(f"\nMultiplicative group for Z_{n}")
print ("* | ",end="")
for i in range(0,n): print(i,end=" ")
print ("\n-------")
for i in range(0,n):
print (i,end=" | ")
for j in range(0,n):
print((i*j)%n,end=" ")
print()
And, so, for Z_p, we need to use a prime number (p), otherwise, we will not be able to produce unique outputs for all the values of 0 to p-1 for additive and multiplication operations. If we thus has eight-bit values, the nearest prime number is 251. So, what would we do for the values from 251 to 255? Galois solved with his Galois fields, and which used polynomials for operations.
GF(2²)
For two-bit values, we can represent the values as polynomials:
00 = 0
01 = 1
10 = x
11 = x+1
Now, we can add to get:
00 + 00 -> 0
00 + 01 -> 0 +1 = 1
00 + 10 -> 0 +x = x
00 + 11 -> 0 + (x+1) = x+1
01 + 00 -> 1 + 0 = 1
01 + 01 -> 1+1 = 0
01 + 10 -> 1+x = 1+x
01 + 11 -> 1+ (x+1) = x
10 + 00 -> x+ 0 = 1
10 + 01 -> x+1 = x+1
10 + 10 -> x+x = 0
10 + 11 -> x+ (x+1) = 1
11 + 00 -> (x+1) + 0 = x+1
11 + 01 -> (x+1)+1 = x
11 + 10 -> (x+1)+x = 1
11 + 11 -> (x+1)+ (x+1) = 0
For this we are using an EX-OR operation, and so that 1+1 =0 and x+x=0. The operations then become [here]:
Irreducible Polynomial:
Additive group for GF(2^2)
+ | 0 1 2 3
-------
0 | [ ][ 1 ][ 1x ][ 1x + 1 ]
1 | [ 1 ][ ][ 1x + 1 ][ 1x ]
2 | [ 1x ][ 1x + 1 ][ ][ 1 ]
3 | [ 1x + 1 ][ 1x ][ 1 ][ ]In terms of numeric values we get:
+ | 0 1 2 3
-----------
0 | 0 1 2 3
1 | 1 0 3 2
2 | 2 3 0 1
3 | 3 2 1 0Everything looks good here, and so we have an additive property. Now let’s try multiplication:
00 + 00 -> 0
00 + 01 -> 0 +1 = 1
00 + 10 -> 0 +x = x
00 + 11 -> 0 + (x+1) = x+1
01 * 00 -> 1 * 0 = 0
01 * 01 -> 1*1 = 1
01 * 10 -> 1*x = x
01 * 11 -> 1* (x+1) = x+1
10 * 00 -> x* 0 = 0
10 * 01 -> x*1 = x
10 * 10 -> x*x = x²
10 * 11 -> x* (x+1) = x²+x
11 * 00 -> (x+1) *0 = 0
11 * 01 -> (x+1)*1 = x+1
11 * 10 -> (x+1)*x = x²+x
11 * 11 -> (x+1)* (x+1) = x²+x+x+1=x²+1
Now we get a result with x² and must get rid of this in order to stay within the region of 00 to 11. Using a Galois field, note the remainder by dividing by an irreducible polynomial (and which cannot be factorized). For n-bits, we need a polynomial with an N power. The first three irreducible polynomials are x, x+1 and x²+x+1:
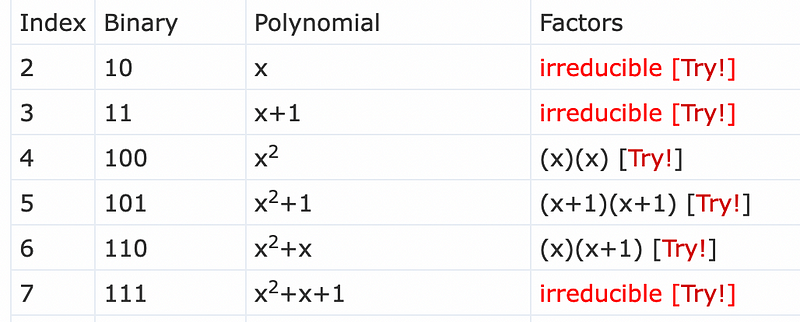
In this case, we can use x²+x+1. Thus for x²+x, we get:
1
-------------
x^2 + x + 1 | x^2 + x
x^2 + x + 1
-----------
1and gives a remainder of 1. We now get [here]:
Multiplicative group for GF(2^3)
+ | 0 1 2 3
-------
0 | [ ][ ][ ][ ]
1 | [ ][ 1 ][ 1x ][ 1x + 1 ]
2 | [ ][ 1x ][ 1x + 1 ][ 1 ]
3 | [ ][ 1x + 1 ][ 1 ][ 1x ]Converting these to integers we get:
Multiplicative group for GF(2^3)
+ | 0 1 2 3
-------
0 | 0 0 0 0
1 | 0 1 2 3
2 | 0 2 3 1
3 | 0 3 1 2And we can see that all the outputs are generated.
GF(2³)
And, so, GF(2²) works well. Now let’s try GF(2³). For this, we now have three bits for our values, and which can range from 0 to 7. With 110 we can represent it as x²+x. We will now use this program to generate the output [here]:
from galois_field import GFpn
import math
import sys
def bits(num):
bit_list = [(num >> shift_ind) & 1
for shift_ind in range(num.bit_length())] # little endian
bit_list.reverse() # big endian
return(bit_list)
ip4=[1,0,0,1,1] # irreducible polynomial for GF(2^4) - x^4+x+1
ip3=[1,0,1,1] # irreducible polynomial for GF(2^3) - x^3+x+1
ip2=[1,1,1] # irreducible polynomial for GF(2^2) - x^2+x+1
p=3
if (len(sys.argv)>1):
p=int(sys.argv[1])
ip=ip2
if (p==2):
ip=ip2
elif (p==3):
ip=ip3
elif (p==4):
ip=ip4
gf = GFpn(2,ip )
n=2**p
ip_str=gf.elm(ip)
print("Irreducible Polynomial: ",ip)
print(f"Additive group for GF(2^p)")
print ("+ | ",end="")
for i in range(0,n): print(i,end=" ")
print ("\n-------")
for i in range(0,n):
print (i,end=" | ")
for j in range(0,n):
res=gf.elm(bits(i))+gf.elm(bits(j))
print("[",res,"]",end="")
print()
print(f"Multiplicative group for GF(2^3)")
print ("+ | ",end="")
for i in range(0,n): print(i,end=" ")
print ("\n-------")
for i in range(0,n):
print (i,end=" | ")
for j in range(0,n):
res=gf.elm(bits(i))*gf.elm(bits(j))
print("[",res,"]",end="")
print()
We can then run for GF(2³) [here]:
Additive group for GF(2^3)
+ | 0 1 2 3 4 5 6 7
--------------------------------------------------------------------------
0 | [ 0 ] [ 1 ] [ 1x ] [ 1x + 1 ] [ 1x^2 ] [ 1x^2 + 1 ] [ 1x^2 + 1x ] [ 1x^2 + 1x + 1 ]
1 | [ 1 ] [ 0 ] [ 1x + 1 ] [ 1x ] [ 1x^2 + 1 ] [ 1x^2 ] [ 1x^2 + 1x + 1 ] [ 1x^2 + 1x ]
2 | [ 1x ] [ 1x + 1 ] [ 0 ] [ 1 ] [ 1x^2 + 1x ] [ 1x^2 + 1x + 1 ] [ 1x^2 ] [ 1x^2 + 1 ]
3 | [ 1x + 1 ] [ 1x ] [ 1 ] [ 0 ] [ 1x^2 + 1x + 1 ] [ 1x^2 + 1x ] [ 1x^2 + 1 ] [ 1x^2 ]
4 | [ 1x^2 ] [ 1x^2 + 1 ] [ 1x^2 + 1x ] [ 1x^2 + 1x + 1 ] [ 0 ] [ 1 ] [ 1x ] [ 1x + 1 ]
5 | [ 1x^2 + 1 ] [ 1x^2 ] [ 1x^2 + 1x + 1 ] [ 1x^2 + 1x ] [ 1 ] [ 0 ] [ 1x + 1 ] [ 1x ]
6 | [ 1x^2 + 1x ] [ 1x^2 + 1x + 1 ] [ 1x^2 ] [ 1x^2 + 1 ] [ 1x ] [ 1x + 1 ] [ 0 ] [ 1 ]
7 | [ 1x^2 + 1x + 1 ] [ 1x^2 + 1x ] [ 1x^2 + 1 ] [ 1x^2 ] [ 1x + 1 ] [ 1x ] [ 1 ] [ 0 ]
Multiplicative group for GF(2^3)
+ | 0 1 2 3 4 5 6 7
--------------------------------------------------------------------------
0 | [ 0 ] [ 0 ] [ 0] [ 0 ] [ 0 ] [ 0 ] [ 0 ] [ 0 ]
1 | [ 0 ] [ 1 ] [ 1x ] [ 1x + 1 ] [ 1x^2 ] [ 1x^2 + 1 ] [ 1x^2 + 1x ] [ 1x^2 + 1x + 1 ]
2 | [ 0 ] [ 1x ] [ 1x^2 ] [ 1x^2 + 1x ] [ 1x + 1 ] [ 1 ] [ 1x^2 + 1x + 1 ] [ 1x^2 + 1 ]
3 | [ 0 ] [ 1x + 1 ] [ 1x^2 + 1x ] [ 1x^2 + 1 ] [ 1x^2 + 1x + 1 ] [ 1x^2 ] [ 1 ] [ 1x ]
4 | [ 0 ] [ 1x^2 ] [ 1x + 1 ] [ 1x^2 + 1x + 1 ] [ 1x^2 + 1x ] [ 1x ] [ 1x^2 + 1 ] [ 1 ]
5 | [ 0 ] [ 1x^2 + 1 ] [ 1 ] [ 1x^2 ] [ 1x ] [ 1x^2 + 1x + 1 ] [ 1x + 1 ] [ 1x^2 + 1x ]
6 | [ 0 ] [ 1x^2 + 1x ] [ 1x^2 + 1x + 1 ] [ 1 ] [ 1x^2 + 1 ] [ 1x + 1 ] [ 1x ] [ 1x^2 ]
7 | [ 0 ] [ 1x^2 + 1x + 1 ] [ 1x^2 + 1 ] [ 1x ] [ 1 ] [ 1x^2 + 1x ] [ 1x^2 ] [ 1x + 1 ] This translates to [here]:
Additive group for GF(2^3)
+ | 0 1 2 3 4 5 6 7
--------------------
0 | 0 1 2 3 4 5 6 7
1 | 1 0 3 2 5 4 7 6
2 | 2 3 0 1 6 7 4 5
3 | 3 2 1 0 7 6 5 4
4 | 4 5 6 7 0 1 2 3
5 | 5 4 7 6 1 0 3 2
6 | 6 7 4 5 2 3 0 1
7 | 7 6 5 4 3 2 1 0
Multiplicative group for GF(2^3)
+ | 0 1 2 3 4 5 6 7
---------------------
0 | 0 0 0 0 0 0 0 0
1 | 0 1 2 3 4 5 6 7
2 | 0 2 4 6 3 1 7 5
3 | 0 3 6 5 7 4 1 2
4 | 0 4 3 7 6 2 5 1
5 | 0 5 1 4 2 7 3 6
6 | 0 6 7 1 5 3 2 4
7 | 0 7 5 2 1 6 4 3We can see that GF(2³) now produces all of the outputs that are possible, such as where 2*5 =1. The value of 1 is the multiplicative inverse (division), and so the multiplicative inverse of 1 is 1, the multiplicative inverse of 2 is 5, the multiplicative inverse of 3 is 6, the multiplicative inverse of 4 is 7, the multiplicative inverse of 6 is 3, and the multiplicative inverse of 7 is 4. This means that we go through all the possible inputs and can get all the possible outputs. For the additive inverse (subtraction), we locate the zero values, and so the additive inverse of 1 is 1, and the additive inverse of 2 is 2.
GF(2⁴)
We can keep going with GF(p^n), and where p is a prime and n is a positive integer and each of the fields with work for us. Overall, we need to find the correct irreducible polynomial [here]. Now that we have 4 bits we need an irreducible polynomial of x⁴+x+1:

A sample run of the program gives:
Irreducible Polynomial: [1, 0, 0, 1, 1]
Additive group for GF(2^p)
+ | 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15
-------
0 | [ ][ 1 ][ 1x ][ 1x + 1 ][ 1x^2 ][ 1x^2 + 1 ][ 1x^2 + 1x ][ 1x^2 + 1x + 1 ][ 1x^3 ][ 1x^3 + 1 ][ 1x^3 + 1x ][ 1x^3 + 1x + 1 ][ 1x^3 + 1x^2 ][ 1x^3 + 1x^2 + 1 ][ 1x^3 + 1x^2 + 1x ][ 1x^3 + 1x^2 + 1x + 1 ]
1 | [ 1 ][ ][ 1x + 1 ][ 1x ][ 1x^2 + 1 ][ 1x^2 ][ 1x^2 + 1x + 1 ][ 1x^2 + 1x ][ 1x^3 + 1 ][ 1x^3 ][ 1x^3 + 1x + 1 ][ 1x^3 + 1x ][ 1x^3 + 1x^2 + 1 ][ 1x^3 + 1x^2 ][ 1x^3 + 1x^2 + 1x + 1 ][ 1x^3 + 1x^2 + 1x ]
2 | [ 1x ][ 1x + 1 ][ ][ 1 ][ 1x^2 + 1x ][ 1x^2 + 1x + 1 ][ 1x^2 ][ 1x^2 + 1 ][ 1x^3 + 1x ][ 1x^3 + 1x + 1 ][ 1x^3 ][ 1x^3 + 1 ][ 1x^3 + 1x^2 + 1x ][ 1x^3 + 1x^2 + 1x + 1 ][ 1x^3 + 1x^2 ][ 1x^3 + 1x^2 + 1 ]
3 | [ 1x + 1 ][ 1x ][ 1 ][ ][ 1x^2 + 1x + 1 ][ 1x^2 + 1x ][ 1x^2 + 1 ][ 1x^2 ][ 1x^3 + 1x + 1 ][ 1x^3 + 1x ][ 1x^3 + 1 ][ 1x^3 ][ 1x^3 + 1x^2 + 1x + 1 ][ 1x^3 + 1x^2 + 1x ][ 1x^3 + 1x^2 + 1 ][ 1x^3 + 1x^2 ]
4 | [ 1x^2 ][ 1x^2 + 1 ][ 1x^2 + 1x ][ 1x^2 + 1x + 1 ][ ][ 1 ][ 1x ][ 1x + 1 ][ 1x^3 + 1x^2 ][ 1x^3 + 1x^2 + 1 ][ 1x^3 + 1x^2 + 1x ][ 1x^3 + 1x^2 + 1x + 1 ][ 1x^3 ][ 1x^3 + 1 ][ 1x^3 + 1x ][ 1x^3 + 1x + 1 ]
5 | [ 1x^2 + 1 ][ 1x^2 ][ 1x^2 + 1x + 1 ][ 1x^2 + 1x ][ 1 ][ ][ 1x + 1 ][ 1x ][ 1x^3 + 1x^2 + 1 ][ 1x^3 + 1x^2 ][ 1x^3 + 1x^2 + 1x + 1 ][ 1x^3 + 1x^2 + 1x ][ 1x^3 + 1 ][ 1x^3 ][ 1x^3 + 1x + 1 ][ 1x^3 + 1x ]
6 | [ 1x^2 + 1x ][ 1x^2 + 1x + 1 ][ 1x^2 ][ 1x^2 + 1 ][ 1x ][ 1x + 1 ][ ][ 1 ][ 1x^3 + 1x^2 + 1x ][ 1x^3 + 1x^2 + 1x + 1 ][ 1x^3 + 1x^2 ][ 1x^3 + 1x^2 + 1 ][ 1x^3 + 1x ][ 1x^3 + 1x + 1 ][ 1x^3 ][ 1x^3 + 1 ]
7 | [ 1x^2 + 1x + 1 ][ 1x^2 + 1x ][ 1x^2 + 1 ][ 1x^2 ][ 1x + 1 ][ 1x ][ 1 ][ ][ 1x^3 + 1x^2 + 1x + 1 ][ 1x^3 + 1x^2 + 1x ][ 1x^3 + 1x^2 + 1 ][ 1x^3 + 1x^2 ][ 1x^3 + 1x + 1 ][ 1x^3 + 1x ][ 1x^3 + 1 ][ 1x^3 ]
8 | [ 1x^3 ][ 1x^3 + 1 ][ 1x^3 + 1x ][ 1x^3 + 1x + 1 ][ 1x^3 + 1x^2 ][ 1x^3 + 1x^2 + 1 ][ 1x^3 + 1x^2 + 1x ][ 1x^3 + 1x^2 + 1x + 1 ][ ][ 1 ][ 1x ][ 1x + 1 ][ 1x^2 ][ 1x^2 + 1 ][ 1x^2 + 1x ][ 1x^2 + 1x + 1 ]
9 | [ 1x^3 + 1 ][ 1x^3 ][ 1x^3 + 1x + 1 ][ 1x^3 + 1x ][ 1x^3 + 1x^2 + 1 ][ 1x^3 + 1x^2 ][ 1x^3 + 1x^2 + 1x + 1 ][ 1x^3 + 1x^2 + 1x ][ 1 ][ ][ 1x + 1 ][ 1x ][ 1x^2 + 1 ][ 1x^2 ][ 1x^2 + 1x + 1 ][ 1x^2 + 1x ]
10 | [ 1x^3 + 1x ][ 1x^3 + 1x + 1 ][ 1x^3 ][ 1x^3 + 1 ][ 1x^3 + 1x^2 + 1x ][ 1x^3 + 1x^2 + 1x + 1 ][ 1x^3 + 1x^2 ][ 1x^3 + 1x^2 + 1 ][ 1x ][ 1x + 1 ][ ][ 1 ][ 1x^2 + 1x ][ 1x^2 + 1x + 1 ][ 1x^2 ][ 1x^2 + 1 ]
11 | [ 1x^3 + 1x + 1 ][ 1x^3 + 1x ][ 1x^3 + 1 ][ 1x^3 ][ 1x^3 + 1x^2 + 1x + 1 ][ 1x^3 + 1x^2 + 1x ][ 1x^3 + 1x^2 + 1 ][ 1x^3 + 1x^2 ][ 1x + 1 ][ 1x ][ 1 ][ ][ 1x^2 + 1x + 1 ][ 1x^2 + 1x ][ 1x^2 + 1 ][ 1x^2 ]
12 | [ 1x^3 + 1x^2 ][ 1x^3 + 1x^2 + 1 ][ 1x^3 + 1x^2 + 1x ][ 1x^3 + 1x^2 + 1x + 1 ][ 1x^3 ][ 1x^3 + 1 ][ 1x^3 + 1x ][ 1x^3 + 1x + 1 ][ 1x^2 ][ 1x^2 + 1 ][ 1x^2 + 1x ][ 1x^2 + 1x + 1 ][ ][ 1 ][ 1x ][ 1x + 1 ]
13 | [ 1x^3 + 1x^2 + 1 ][ 1x^3 + 1x^2 ][ 1x^3 + 1x^2 + 1x + 1 ][ 1x^3 + 1x^2 + 1x ][ 1x^3 + 1 ][ 1x^3 ][ 1x^3 + 1x + 1 ][ 1x^3 + 1x ][ 1x^2 + 1 ][ 1x^2 ][ 1x^2 + 1x + 1 ][ 1x^2 + 1x ][ 1 ][ ][ 1x + 1 ][ 1x ]
14 | [ 1x^3 + 1x^2 + 1x ][ 1x^3 + 1x^2 + 1x + 1 ][ 1x^3 + 1x^2 ][ 1x^3 + 1x^2 + 1 ][ 1x^3 + 1x ][ 1x^3 + 1x + 1 ][ 1x^3 ][ 1x^3 + 1 ][ 1x^2 + 1x ][ 1x^2 + 1x + 1 ][ 1x^2 ][ 1x^2 + 1 ][ 1x ][ 1x + 1 ][ ][ 1 ]
15 | [ 1x^3 + 1x^2 + 1x + 1 ][ 1x^3 + 1x^2 + 1x ][ 1x^3 + 1x^2 + 1 ][ 1x^3 + 1x^2 ][ 1x^3 + 1x + 1 ][ 1x^3 + 1x ][ 1x^3 + 1 ][ 1x^3 ][ 1x^2 + 1x + 1 ][ 1x^2 + 1x ][ 1x^2 + 1 ][ 1x^2 ][ 1x + 1 ][ 1x ][ 1 ][ ]
Multiplicative group for GF(2^3)
+ | 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15
-------
0 | [ ][ ][ ][ ][ ][ ][ ][ ][ ][ ][ ][ ][ ][ ][ ][ ]
1 | [ ][ 1 ][ 1x ][ 1x + 1 ][ 1x^2 ][ 1x^2 + 1 ][ 1x^2 + 1x ][ 1x^2 + 1x + 1 ][ 1x^3 ][ 1x^3 + 1 ][ 1x^3 + 1x ][ 1x^3 + 1x + 1 ][ 1x^3 + 1x^2 ][ 1x^3 + 1x^2 + 1 ][ 1x^3 + 1x^2 + 1x ][ 1x^3 + 1x^2 + 1x + 1 ]
2 | [ ][ 1x ][ 1x^2 ][ 1x^2 + 1x ][ 1x^3 ][ 1x^3 + 1x ][ 1x^3 + 1x^2 ][ 1x^3 + 1x^2 + 1x ][ 1x + 1 ][ 1 ][ 1x^2 + 1x + 1 ][ 1x^2 + 1 ][ 1x^3 + 1x + 1 ][ 1x^3 + 1 ][ 1x^3 + 1x^2 + 1x + 1 ][ 1x^3 + 1x^2 + 1 ]
3 | [ ][ 1x + 1 ][ 1x^2 + 1x ][ 1x^2 + 1 ][ 1x^3 + 1x^2 ][ 1x^3 + 1x^2 + 1x + 1 ][ 1x^3 + 1x ][ 1x^3 + 1 ][ 1x^3 + 1x + 1 ][ 1x^3 ][ 1x^3 + 1x^2 + 1 ][ 1x^3 + 1x^2 + 1x ][ 1x^2 + 1x + 1 ][ 1x^2 ][ 1 ][ 1x ]
4 | [ ][ 1x^2 ][ 1x^3 ][ 1x^3 + 1x^2 ][ 1x + 1 ][ 1x^2 + 1x + 1 ][ 1x^3 + 1x + 1 ][ 1x^3 + 1x^2 + 1x + 1 ][ 1x^2 + 1x ][ 1x ][ 1x^3 + 1x^2 + 1x ][ 1x^3 + 1x ][ 1x^2 + 1 ][ 1 ][ 1x^3 + 1x^2 + 1 ][ 1x^3 + 1 ]
5 | [ ][ 1x^2 + 1 ][ 1x^3 + 1x ][ 1x^3 + 1x^2 + 1x + 1 ][ 1x^2 + 1x + 1 ][ 1x ][ 1x^3 + 1x^2 + 1 ][ 1x^3 ][ 1x^3 + 1x^2 + 1x ][ 1x^3 + 1x + 1 ][ 1x^2 ][ 1 ][ 1x^3 + 1 ][ 1x^3 + 1x^2 ][ 1x + 1 ][ 1x^2 + 1x ]
6 | [ ][ 1x^2 + 1x ][ 1x^3 + 1x^2 ][ 1x^3 + 1x ][ 1x^3 + 1x + 1 ][ 1x^3 + 1x^2 + 1 ][ 1x^2 + 1x + 1 ][ 1 ][ 1x^2 + 1 ][ 1x + 1 ][ 1x^3 + 1 ][ 1x^3 + 1x^2 + 1x + 1 ][ 1x^3 + 1x^2 + 1x ][ 1x^3 ][ 1x ][ 1x^2 ]
7 | [ ][ 1x^2 + 1x + 1 ][ 1x^3 + 1x^2 + 1x ][ 1x^3 + 1 ][ 1x^3 + 1x^2 + 1x + 1 ][ 1x^3 ][ 1 ][ 1x^2 + 1x ][ 1x^3 + 1x^2 + 1 ][ 1x^3 + 1x ][ 1x + 1 ][ 1x^2 ][ 1x ][ 1x^2 + 1 ][ 1x^3 + 1x^2 ][ 1x^3 + 1x + 1 ]
8 | [ ][ 1x^3 ][ 1x + 1 ][ 1x^3 + 1x + 1 ][ 1x^2 + 1x ][ 1x^3 + 1x^2 + 1x ][ 1x^2 + 1 ][ 1x^3 + 1x^2 + 1 ][ 1x^3 + 1x^2 ][ 1x^2 ][ 1x^3 + 1x^2 + 1x + 1 ][ 1x^2 + 1x + 1 ][ 1x^3 + 1x ][ 1x ][ 1x^3 + 1 ][ 1 ]
9 | [ ][ 1x^3 + 1 ][ 1 ][ 1x^3 ][ 1x ][ 1x^3 + 1x + 1 ][ 1x + 1 ][ 1x^3 + 1x ][ 1x^2 ][ 1x^3 + 1x^2 + 1 ][ 1x^2 + 1 ][ 1x^3 + 1x^2 ][ 1x^2 + 1x ][ 1x^3 + 1x^2 + 1x + 1 ][ 1x^2 + 1x + 1 ][ 1x^3 + 1x^2 + 1x ]
10 | [ ][ 1x^3 + 1x ][ 1x^2 + 1x + 1 ][ 1x^3 + 1x^2 + 1 ][ 1x^3 + 1x^2 + 1x ][ 1x^2 ][ 1x^3 + 1 ][ 1x + 1 ][ 1x^3 + 1x^2 + 1x + 1 ][ 1x^2 + 1 ][ 1x^3 ][ 1x ][ 1 ][ 1x^3 + 1x + 1 ][ 1x^2 + 1x ][ 1x^3 + 1x^2 ]
11 | [ ][ 1x^3 + 1x + 1 ][ 1x^2 + 1 ][ 1x^3 + 1x^2 + 1x ][ 1x^3 + 1x ][ 1 ][ 1x^3 + 1x^2 + 1x + 1 ][ 1x^2 ][ 1x^2 + 1x + 1 ][ 1x^3 + 1x^2 ][ 1x ][ 1x^3 + 1 ][ 1x^3 + 1x^2 + 1 ][ 1x^2 + 1x ][ 1x^3 ][ 1x + 1 ]
12 | [ ][ 1x^3 + 1x^2 ][ 1x^3 + 1x + 1 ][ 1x^2 + 1x + 1 ][ 1x^2 + 1 ][ 1x^3 + 1 ][ 1x^3 + 1x^2 + 1x ][ 1x ][ 1x^3 + 1x ][ 1x^2 + 1x ][ 1 ][ 1x^3 + 1x^2 + 1 ][ 1x^3 + 1x^2 + 1x + 1 ][ 1x + 1 ][ 1x^2 ][ 1x^3 ]
13 | [ ][ 1x^3 + 1x^2 + 1 ][ 1x^3 + 1 ][ 1x^2 ][ 1 ][ 1x^3 + 1x^2 ][ 1x^3 ][ 1x^2 + 1 ][ 1x ][ 1x^3 + 1x^2 + 1x + 1 ][ 1x^3 + 1x + 1 ][ 1x^2 + 1x ][ 1x + 1 ][ 1x^3 + 1x^2 + 1x ][ 1x^3 + 1x ][ 1x^2 + 1x + 1 ]
14 | [ ][ 1x^3 + 1x^2 + 1x ][ 1x^3 + 1x^2 + 1x + 1 ][ 1 ][ 1x^3 + 1x^2 + 1 ][ 1x + 1 ][ 1x ][ 1x^3 + 1x^2 ][ 1x^3 + 1 ][ 1x^2 + 1x + 1 ][ 1x^2 + 1x ][ 1x^3 ][ 1x^2 ][ 1x^3 + 1x ][ 1x^3 + 1x + 1 ][ 1x^2 + 1 ]
15 | [ ][ 1x^3 + 1x^2 + 1x + 1 ][ 1x^3 + 1x^2 + 1 ][ 1x ][ 1x^3 + 1 ][ 1x^2 + 1x ][ 1x^2 ][ 1x^3 + 1x + 1 ][ 1 ][ 1x^3 + 1x^2 + 1x ][ 1x^3 + 1x^2 ][ 1x + 1 ][ 1x^3 ][ 1x^2 + 1x + 1 ][ 1x^2 + 1 ][ 1x^3 + 1x ]You can check all of these values, and will find that all the possible outputs are generated for additive and multiplication groups and that each has a multiplicative inverse ([1]) and an additive inverse ([ ]).
So what?
Z_p doesn’t support use well for addition and multiplication as p needs to be a prime number, but GF(p^n) comes to our rescue, and where we can use GF(2³) for 3-bit values and GF(2⁸) for 8-bit values, and scale to any range that we need. And we have found our solution in GF(p^n). Obviously, we don’t need to use 2 for p, and can use any prime number we want. And when dealing with 8-bit values, such as in AES, we use x⁸+x⁴+x³+x+1:

Apart from their usage in AES, Galois fields really come alive in lattice cryptography, and where we use polynomial values to represent points in a lattice. We then operate on these with add, multiply, and multiplicative inverse to perform our cryptographic operations. These are all done by using the irreducible polynomials of our maximum polynomial power.
So, Galois has saved cybersecurity from the Grinch (aka Quantum Computers).