Why Is Symmetric Key Encryption So Much Faster Than Asymmetric (Public) Key?

Why Is Symmetric Key Encryption So Much Faster Than Asymmetric (Public) Key?
Remember as a child when you said something that your teachers or parents said, “That’s a silly question. It just is!”. Well, children often ask some of the best questions, as they often don’t take things for granted. As a good innovator and/or researcher, you need to continually ask question, and, especially, for things that might seem obvious.
So, why is symmetric key so much faster than asymmetric key. Well, asymmetric key encryption uses fairly large prime numbers, and which makes the operations fairly complex. In RSA, for example, we have to operate with a modulus, and which is often made up to two 1,024 bit prime numbers. The values we must process then up having 2,048 bits. We thus need many operations just to compute a single value.
In symmetric key encryption, such as with AES, we use a much simplier way of operating on our data: Galois Fields (GF). With this, we can constrain the values we operate on to just 4 or 8 bits. Every operation with have in a GF, such as for add, subtract and multiply, can be easily reversed, such as for subtract, add and divide. Thus in symmetric key, we might multiply by a given value (and use a part of our encryption key) and then to decrypt we can then divide by the same value (and the same part of the key). The division is actually done by finding the inverse of a value, and then multiply. Overall, these operations are done with polynomial operations, and which are efficient in their operation. In fact, lattice methods use the same approach.
Let’s take a few examples For two-bit values (GF2²), we can represent the values as polynomials:
00 = 0
01 = 1
10 = x
11 = x+1Now, we can add to get:
00 + 00 -> 0
00 + 01 -> 0 +1 = 1
00 + 10 -> 0 +x = x
00 + 11 -> 0 + (x+1) = x+1
01 + 00 -> 1 + 0 = 1
01 + 01 -> 1+1 = 0
01 + 10 -> 1+x = 1+x
01 + 11 -> 1+ (x+1) = x
10 + 00 -> x+ 0 = 1
10 + 01 -> x+1 = x+1
10 + 10 -> x+x = 0
10 + 11 -> x+ (x+1) = 1
11 + 00 -> (x+1) + 0 = x+1
11 + 01 -> (x+1)+1 = x
11 + 10 -> (x+1)+x = 1
11 + 11 -> (x+1)+ (x+1) = 0For this we are using an EX-OR operation, and so that 1+1 =0 and x+x=0. The operations then become:
Irreducible Polynomial:
Additive group for GF(2^2)
+ | 0 1 2 3
-------
0 | [ ][ 1 ][ 1x ][ 1x + 1 ]
1 | [ 1 ][ ][ 1x + 1 ][ 1x ]
2 | [ 1x ][ 1x + 1 ][ ][ 1 ]
3 | [ 1x + 1 ][ 1x ][ 1 ][ ]In terms, of numeric values, we get:
+ | 0 1 2 3
-----------
0 | 0 1 2 3
1 | 1 0 3 2
2 | 2 3 0 1
3 | 3 2 1 0Everything looks good here, and so we have an additive property. Now let’s try multiplication:
00 * 00 -> 0
00 * 01 -> 0 * 1 = 0
00 * 10 -> 0 * x = 0
00 * 11 -> 0 * (x+1) = 0
01 * 00 -> 1 * 0 = 0
01 * 01 -> 1*1 = 1
01 * 10 -> 1*x = x
01 * 11 -> 1* (x+1) = x+1
10 * 00 -> x* 0 = 0
10 * 01 -> x*1 = x
10 * 10 -> x*x = x²
10 * 11 -> x* (x+1) = x²+x
11 * 00 -> (x+1) *0 = 0
11 * 01 -> (x+1)*1 = x+1
11 * 10 -> (x+1)*x = x²+x
11 * 11 -> (x+1)* (x+1) = x²+x+x+1=x²+1Now we get a result with x² and must get rid of this in order to stay within the region of 00 to 11. Using a Galois field, note the remainder by dividing by an irreducible polynomial (and which cannot be factorized). For n-bits, we need a polynomial with n as the highest power. The first three irreducible polynomials are x, x+1 and x²+x+1:
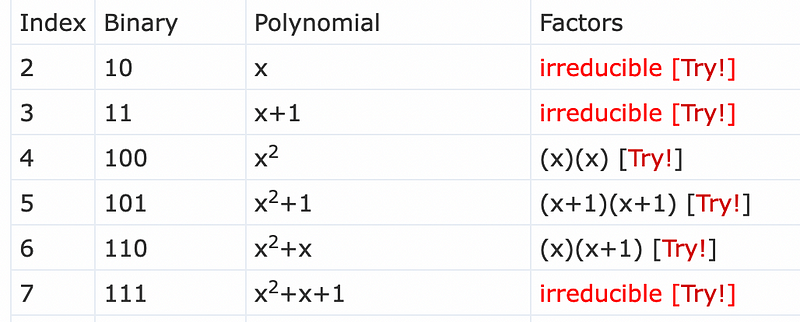
In this case, we can use x²+x+1. Thus for x²+x, we get:
1
-------------
x^2 + x + 1 | x^2 + x
x^2 + x + 1
-----------
1and gives a remainder of 1. We now get:
Multiplicative group for GF(2^3)
+ | 0 1 2 3
-------
0 | [ ][ ][ ][ ]
1 | [ ][ 1 ][ 1x ][ 1x + 1 ]
2 | [ ][ 1x ][ 1x + 1 ][ 1 ]
3 | [ ][ 1x + 1 ][ 1 ][ 1x ]Converting these into integers, we get:
Multiplicative group for GF(2^3)
+ | 0 1 2 3
-------
0 | 0 0 0 0
1 | 0 1 2 3
2 | 0 2 3 1
3 | 0 3 1 2And we can see that all the outputs are generated.
Additive Group — GF(p^n)
If we use this program [here]:
import galois
import sys
import io
p=2
n=2
if (len(sys.argv)>1):
p=int(sys.argv[1])
if (len(sys.argv)>2):
n=int(sys.argv[2])
GF = galois.GF(p**n)
stdout = sys.stdout
f = io.StringIO()
print(f"Additive group for GF({p}^{n})")
print ("+ | ",end="")
for i in range(0,p**n): print("{:2}".format(i),end=" ")
print ("\n-------")
for i in range(0,p**n):
print("{:2}".format(i),end="| ")
for j in range(0,p**n):
a = GF(i)
b = GF(j)
print("{:2}".format(a+b),end=" ")
print()
print("{0}".format(f.getvalue()))For GF(2²), we get [here]:
Additive group for GF(2^2)
+ | 0 1 2 3
-------
0| 0 1 2 3
1| 1 0 3 2
2| 2 3 0 1
3| 3 2 1 0and for GF(2³), we get [here]:
Additive group for GF(2^3)
+ | 0 1 2 3 4 5 6 7
-------
0| 0 1 2 3 4 5 6 7
1| 1 0 3 2 5 4 7 6
2| 2 3 0 1 6 7 4 5
3| 3 2 1 0 7 6 5 4
4| 4 5 6 7 0 1 2 3
5| 5 4 7 6 1 0 3 2
6| 6 7 4 5 2 3 0 1
7| 7 6 5 4 3 2 1 0and for GF(2⁴), we get [here]:
Additive group for GF(2^4)
+ | 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15
-------
0| 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15
1| 1 0 3 2 5 4 7 6 9 8 11 10 13 12 15 14
2| 2 3 0 1 6 7 4 5 10 11 8 9 14 15 12 13
3| 3 2 1 0 7 6 5 4 11 10 9 8 15 14 13 12
4| 4 5 6 7 0 1 2 3 12 13 14 15 8 9 10 11
5| 5 4 7 6 1 0 3 2 13 12 15 14 9 8 11 10
6| 6 7 4 5 2 3 0 1 14 15 12 13 10 11 8 9
7| 7 6 5 4 3 2 1 0 15 14 13 12 11 10 9 8
8| 8 9 10 11 12 13 14 15 0 1 2 3 4 5 6 7
9| 9 8 11 10 13 12 15 14 1 0 3 2 5 4 7 6
10| 10 11 8 9 14 15 12 13 2 3 0 1 6 7 4 5
11| 11 10 9 8 15 14 13 12 3 2 1 0 7 6 5 4
12| 12 13 14 15 8 9 10 11 4 5 6 7 0 1 2 3
13| 13 12 15 14 9 8 11 10 5 4 7 6 1 0 3 2
14| 14 15 12 13 10 11 8 9 6 7 4 5 2 3 0 1
15| 15 14 13 12 11 10 9 8 7 6 5 4 3 2 1 0If we need a negative value, we just need to find the “0” value. Also, notice how the range of values is limited to between 0 and 2^{n-1}. The number of bits we use, will then just be n.
Multiplicative Group — GF(p^n)
If we use this program [here], and try GF(2²), we get:
Multiplicative group for GF(2^2)
+ | 0 1 2 3
-------
0| 0 0 0 0
1| 0 1 2 3
2| 0 2 3 1
3| 0 3 1 2and for GF(2³), we get [here]:
Multiplicative group for GF(2^3)
+ | 0 1 2 3 4 5 6 7
-------
0| 0 0 0 0 0 0 0 0
1| 0 1 2 3 4 5 6 7
2| 0 2 4 6 3 1 7 5
3| 0 3 6 5 7 4 1 2
4| 0 4 3 7 6 2 5 1
5| 0 5 1 4 2 7 3 6
6| 0 6 7 1 5 3 2 4
7| 0 7 5 2 1 6 4 3and for GF(2⁴), we get [here]:
Multiplicative group for GF(2^4)
+ | 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15
-------
0| 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0
1| 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15
2| 0 2 4 6 8 10 12 14 3 1 7 5 11 9 15 13
3| 0 3 6 5 12 15 10 9 11 8 13 14 7 4 1 2
4| 0 4 8 12 3 7 11 15 6 2 14 10 5 1 13 9
5| 0 5 10 15 7 2 13 8 14 11 4 1 9 12 3 6
6| 0 6 12 10 11 13 7 1 5 3 9 15 14 8 2 4
7| 0 7 14 9 15 8 1 6 13 10 3 4 2 5 12 11
8| 0 8 3 11 6 14 5 13 12 4 15 7 10 2 9 1
9| 0 9 1 8 2 11 3 10 4 13 5 12 6 15 7 14
10| 0 10 7 13 14 4 9 3 15 5 8 2 1 11 6 12
11| 0 11 5 14 10 1 15 4 7 12 2 9 13 6 8 3
12| 0 12 11 7 5 9 14 2 10 6 1 13 15 3 4 8
13| 0 13 9 4 1 12 8 5 2 15 11 6 3 14 10 7
14| 0 14 15 1 13 3 2 12 9 7 6 8 4 10 11 5
15| 0 15 13 2 9 6 4 11 1 14 12 3 8 7 5 10and for GF(2⁵), we get [here]:
Multiplicative group for GF(2^5)
+ | 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31
-------
0| 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0
1| 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31
2| 0 2 4 6 8 10 12 14 16 18 20 22 24 26 28 30 5 7 1 3 13 15 9 11 21 23 17 19 29 31 25 27
3| 0 3 6 5 12 15 10 9 24 27 30 29 20 23 18 17 21 22 19 16 25 26 31 28 13 14 11 8 1 2 7 4
4| 0 4 8 12 16 20 24 28 5 1 13 9 21 17 29 25 10 14 2 6 26 30 18 22 15 11 7 3 31 27 23 19
5| 0 5 10 15 20 17 30 27 13 8 7 2 25 28 19 22 26 31 16 21 14 11 4 1 23 18 29 24 3 6 9 12
6| 0 6 12 10 24 30 20 18 21 19 25 31 13 11 1 7 15 9 3 5 23 17 27 29 26 28 22 16 2 4 14 8
7| 0 7 14 9 28 27 18 21 29 26 19 20 1 6 15 8 31 24 17 22 3 4 13 10 2 5 12 11 30 25 16 23
8| 0 8 16 24 5 13 21 29 10 2 26 18 15 7 31 23 20 28 4 12 17 25 1 9 30 22 14 6 27 19 11 3
9| 0 9 18 27 1 8 19 26 2 11 16 25 3 10 17 24 4 13 22 31 5 12 23 30 6 15 20 29 7 14 21 28
10| 0 10 20 30 13 7 25 19 26 16 14 4 23 29 3 9 17 27 5 15 28 22 8 2 11 1 31 21 6 12 18 24
11| 0 11 22 29 9 2 31 20 18 25 4 15 27 16 13 6 1 10 23 28 8 3 30 21 19 24 5 14 26 17 12 7
12| 0 12 24 20 21 25 13 1 15 3 23 27 26 22 2 14 30 18 6 10 11 7 19 31 17 29 9 5 4 8 28 16
13| 0 13 26 23 17 28 11 6 7 10 29 16 22 27 12 1 14 3 20 25 31 18 5 8 9 4 19 30 24 21 2 15
14| 0 14 28 18 29 19 1 15 31 17 3 13 2 12 30 16 27 21 7 9 6 8 26 20 4 10 24 22 25 23 5 11
15| 0 15 30 17 25 22 7 8 23 24 9 6 14 1 16 31 11 4 21 26 18 29 12 3 28 19 2 13 5 10 27 20
16| 0 16 5 21 10 26 15 31 20 4 17 1 30 14 27 11 13 29 8 24 7 23 2 18 25 9 28 12 19 3 22 6
17| 0 17 7 22 14 31 9 24 28 13 27 10 18 3 21 4 29 12 26 11 19 2 20 5 1 16 6 23 15 30 8 25
18| 0 18 1 19 2 16 3 17 4 22 5 23 6 20 7 21 8 26 9 27 10 24 11 25 12 30 13 31 14 28 15 29
19| 0 19 3 16 6 21 5 22 12 31 15 28 10 25 9 26 24 11 27 8 30 13 29 14 20 7 23 4 18 1 17 2
20| 0 20 13 25 26 14 23 3 17 5 28 8 11 31 6 18 7 19 10 30 29 9 16 4 22 2 27 15 12 24 1 21
21| 0 21 15 26 30 11 17 4 25 12 22 3 7 18 8 29 23 2 24 13 9 28 6 19 14 27 1 20 16 5 31 10
22| 0 22 9 31 18 4 27 13 1 23 8 30 19 5 26 12 2 20 11 29 16 6 25 15 3 21 10 28 17 7 24 14
23| 0 23 11 28 22 1 29 10 9 30 2 21 31 8 20 3 18 5 25 14 4 19 15 24 27 12 16 7 13 26 6 17
24| 0 24 21 13 15 23 26 2 30 6 11 19 17 9 4 28 25 1 12 20 22 14 3 27 7 31 18 10 8 16 29 5
25| 0 25 23 14 11 18 28 5 22 15 1 24 29 4 10 19 9 16 30 7 2 27 21 12 31 6 8 17 20 13 3 26
26| 0 26 17 11 7 29 22 12 14 20 31 5 9 19 24 2 28 6 13 23 27 1 10 16 18 8 3 25 21 15 4 30
27| 0 27 19 8 3 24 16 11 6 29 21 14 5 30 22 13 12 23 31 4 15 20 28 7 10 17 25 2 9 18 26 1
28| 0 28 29 1 31 3 2 30 27 7 6 26 4 24 25 5 19 15 14 18 12 16 17 13 8 20 21 9 23 11 10 22
29| 0 29 31 2 27 6 4 25 19 14 12 17 8 21 23 10 3 30 28 1 24 5 7 26 16 13 15 18 11 22 20 9
30| 0 30 25 7 23 9 14 16 11 21 18 12 28 2 5 27 22 8 15 17 1 31 24 6 29 3 4 26 10 20 19 13
31| 0 31 27 4 19 12 8 23 3 28 24 7 16 15 11 20 6 25 29 2 21 10 14 17 5 26 30 1 22 9 13 18and for GF(2⁶), we get:
Multiplicative group for GF(2^6)
+ | 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63
-------
0| 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0
1| 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63
2| 0 2 4 6 8 10 12 14 16 18 20 22 24 26 28 30 32 34 36 38 40 42 44 46 48 50 52 54 56 58 60 62 27 25 31 29 19 17 23 21 11 9 15 13 3 1 7 5 59 57 63 61 51 49 55 53 43 41 47 45 35 33 39 37
3| 0 3 6 5 12 15 10 9 24 27 30 29 20 23 18 17 48 51 54 53 60 63 58 57 40 43 46 45 36 39 34 33 59 56 61 62 55 52 49 50 35 32 37 38 47 44 41 42 11 8 13 14 7 4 1 2 19 16 21 22 31 28 25 26
4| 0 4 8 12 16 20 24 28 32 36 40 44 48 52 56 60 27 31 19 23 11 15 3 7 59 63 51 55 43 47 35 39 54 50 62 58 38 34 46 42 22 18 30 26 6 2 14 10 45 41 37 33 61 57 53 49 13 9 5 1 29 25 21 17
5| 0 5 10 15 20 17 30 27 40 45 34 39 60 57 54 51 11 14 1 4 31 26 21 16 35 38 41 44 55 50 61 56 22 19 28 25 2 7 8 13 62 59 52 49 42 47 32 37 29 24 23 18 9 12 3 6 53 48 63 58 33 36 43 46
6| 0 6 12 10 24 30 20 18 48 54 60 58 40 46 36 34 59 61 55 49 35 37 47 41 11 13 7 1 19 21 31 25 45 43 33 39 53 51 57 63 29 27 17 23 5 3 9 15 22 16 26 28 14 8 2 4 38 32 42 44 62 56 50 52
7| 0 7 14 9 28 27 18 21 56 63 54 49 36 35 42 45 43 44 37 34 55 48 57 62 19 20 29 26 15 8 1 6 13 10 3 4 17 22 31 24 53 50 59 60 41 46 39 32 38 33 40 47 58 61 52 51 30 25 16 23 2 5 12 11
8| 0 8 16 24 32 40 48 56 27 19 11 3 59 51 43 35 54 62 38 46 22 30 6 14 45 37 61 53 13 5 29 21 55 63 39 47 23 31 7 15 44 36 60 52 12 4 28 20 1 9 17 25 33 41 49 57 26 18 10 2 58 50 42 34
9| 0 9 18 27 36 45 54 63 19 26 1 8 55 62 37 44 38 47 52 61 2 11 16 25 53 60 39 46 17 24 3 10 23 30 5 12 51 58 33 40 4 13 22 31 32 41 50 59 49 56 35 42 21 28 7 14 34 43 48 57 6 15 20 29
10| 0 10 20 30 40 34 60 54 11 1 31 21 35 41 55 61 22 28 2 8 62 52 42 32 29 23 9 3 53 63 33 43 44 38 56 50 4 14 16 26 39 45 51 57 15 5 27 17 58 48 46 36 18 24 6 12 49 59 37 47 25 19 13 7
11| 0 11 22 29 44 39 58 49 3 8 21 30 47 36 57 50 6 13 16 27 42 33 60 55 5 14 19 24 41 34 63 52 12 7 26 17 32 43 54 61 15 4 25 18 35 40 53 62 10 1 28 23 38 45 48 59 9 2 31 20 37 46 51 56
12| 0 12 24 20 48 60 40 36 59 55 35 47 11 7 19 31 45 33 53 57 29 17 5 9 22 26 14 2 38 42 62 50 1 13 25 21 49 61 41 37 58 54 34 46 10 6 18 30 44 32 52 56 28 16 4 8 23 27 15 3 39 43 63 51
13| 0 13 26 23 52 57 46 35 51 62 41 36 7 10 29 16 61 48 39 42 9 4 19 30 14 3 20 25 58 55 32 45 33 44 59 54 21 24 15 2 18 31 8 5 38 43 60 49 28 17 6 11 40 37 50 63 47 34 53 56 27 22 1 12
14| 0 14 28 18 56 54 36 42 43 37 55 57 19 29 15 1 13 3 17 31 53 59 41 39 38 40 58 52 30 16 2 12 26 20 6 8 34 44 62 48 49 63 45 35 9 7 21 27 23 25 11 5 47 33 51 61 60 50 32 46 4 10 24 22
15| 0 15 30 17 60 51 34 45 35 44 61 50 31 16 1 14 29 18 3 12 33 46 63 48 62 49 32 47 2 13 28 19 58 53 36 43 6 9 24 23 25 22 7 8 37 42 59 52 39 40 57 54 27 20 5 10 4 11 26 21 56 55 38 41
16| 0 16 32 48 27 11 59 43 54 38 22 6 45 61 13 29 55 39 23 7 44 60 12 28 1 17 33 49 26 10 58 42 53 37 21 5 46 62 14 30 3 19 35 51 24 8 56 40 2 18 34 50 25 9 57 41 52 36 20 4 47 63 15 31
17| 0 17 34 51 31 14 61 44 62 47 28 13 33 48 3 18 39 54 5 20 56 41 26 11 25 8 59 42 6 23 36 53 21 4 55 38 10 27 40 57 43 58 9 24 52 37 22 7 50 35 16 1 45 60 15 30 12 29 46 63 19 2 49 32
18| 0 18 36 54 19 1 55 37 38 52 2 16 53 39 17 3 23 5 51 33 4 22 32 50 49 35 21 7 34 48 6 20 46 60 10 24 61 47 25 11 8 26 44 62 27 9 63 45 57 43 29 15 42 56 14 28 31 13 59 41 12 30 40 58
19| 0 19 38 53 23 4 49 34 46 61 8 27 57 42 31 12 7 20 33 50 16 3 54 37 41 58 15 28 62 45 24 11 14 29 40 59 25 10 63 44 32 51 6 21 55 36 17 2 9 26 47 60 30 13 56 43 39 52 1 18 48 35 22 5
20| 0 20 40 60 11 31 35 55 22 2 62 42 29 9 53 33 44 56 4 16 39 51 15 27 58 46 18 6 49 37 25 13 3 23 43 63 8 28 32 52 21 1 61 41 30 10 54 34 47 59 7 19 36 48 12 24 57 45 17 5 50 38 26 14
21| 0 21 42 63 15 26 37 48 30 11 52 33 17 4 59 46 60 41 22 3 51 38 25 12 34 55 8 29 45 56 7 18 35 54 9 28 44 57 6 19 61 40 23 2 50 39 24 13 31 10 53 32 16 5 58 47 1 20 43 62 14 27 36 49
22| 0 22 44 58 3 21 47 57 6 16 42 60 5 19 41 63 12 26 32 54 15 25 35 53 10 28 38 48 9 31 37 51 24 14 52 34 27 13 55 33 30 8 50 36 29 11 49 39 20 2 56 46 23 1 59 45 18 4 62 40 17 7 61 43
23| 0 23 46 57 7 16 41 62 14 25 32 55 9 30 39 48 28 11 50 37 27 12 53 34 18 5 60 43 21 2 59 44 56 47 22 1 63 40 17 6 54 33 24 15 49 38 31 8 36 51 10 29 35 52 13 26 42 61 4 19 45 58 3 20
24| 0 24 48 40 59 35 11 19 45 53 29 5 22 14 38 62 1 25 49 41 58 34 10 18 44 52 28 4 23 15 39 63 2 26 50 42 57 33 9 17 47 55 31 7 20 12 36 60 3 27 51 43 56 32 8 16 46 54 30 6 21 13 37 61
25| 0 25 50 43 63 38 13 20 37 60 23 14 26 3 40 49 17 8 35 58 46 55 28 5 52 45 6 31 11 18 57 32 34 59 16 9 29 4 47 54 7 30 53 44 56 33 10 19 51 42 1 24 12 21 62 39 22 15 36 61 41 48 27 2
26| 0 26 52 46 51 41 7 29 61 39 9 19 14 20 58 32 33 59 21 15 18 8 38 60 28 6 40 50 47 53 27 1 25 3 45 55 42 48 30 4 36 62 16 10 23 13 35 57 56 34 12 22 11 17 63 37 5 31 49 43 54 44 2 24
27| 0 27 54 45 55 44 1 26 53 46 3 24 2 25 52 47 49 42 7 28 6 29 48 43 4 31 50 41 51 40 5 30 57 34 15 20 14 21 56 35 12 23 58 33 59 32 13 22 8 19 62 37 63 36 9 18 61 38 11 16 10 17 60 39
28| 0 28 56 36 43 55 19 15 13 17 53 41 38 58 30 2 26 6 34 62 49 45 9 21 23 11 47 51 60 32 4 24 52 40 12 16 31 3 39 59 57 37 1 29 18 14 42 54 46 50 22 10 5 25 61 33 35 63 27 7 8 20 48 44
29| 0 29 58 39 47 50 21 8 5 24 63 34 42 55 16 13 10 23 48 45 37 56 31 2 15 18 53 40 32 61 26 7 20 9 46 51 59 38 1 28 17 12 43 54 62 35 4 25 30 3 36 57 49 44 11 22 27 6 33 60 52 41 14 19
30| 0 30 60 34 35 61 31 1 29 3 33 63 62 32 2 28 58 36 6 24 25 7 37 59 39 57 27 5 4 26 56 38 47 49 19 13 12 18 48 46 50 44 14 16 17 15 45 51 21 11 41 55 54 40 10 20 8 22 52 42 43 53 23 9
31| 0 31 62 33 39 56 25 6 21 10 43 52 50 45 12 19 42 53 20 11 13 18 51 44 63 32 1 30 24 7 38 57 15 16 49 46 40 55 22 9 26 5 36 59 61 34 3 28 37 58 27 4 2 29 60 35 48 47 14 17 23 8 41 54
32| 0 32 27 59 54 22 45 13 55 23 44 12 1 33 26 58 53 21 46 14 3 35 24 56 2 34 25 57 52 20 47 15 49 17 42 10 7 39 28 60 6 38 29 61 48 16 43 11 4 36 31 63 50 18 41 9 51 19 40 8 5 37 30 62
33| 0 33 25 56 50 19 43 10 63 30 38 7 13 44 20 53 37 4 60 29 23 54 14 47 26 59 3 34 40 9 49 16 17 48 8 41 35 2 58 27 46 15 55 22 28 61 5 36 52 21 45 12 6 39 31 62 11 42 18 51 57 24 32 1
34| 0 34 31 61 62 28 33 3 39 5 56 26 25 59 6 36 21 55 10 40 43 9 52 22 50 16 45 15 12 46 19 49 42 8 53 23 20 54 11 41 13 47 18 48 51 17 44 14 63 29 32 2 1 35 30 60 24 58 7 37 38 4 57 27
35| 0 35 29 62 58 25 39 4 47 12 50 17 21 54 8 43 5 38 24 59 63 28 34 1 42 9 55 20 16 51 13 46 10 41 23 52 48 19 45 14 37 6 56 27 31 60 2 33 15 44 18 49 53 22 40 11 32 3 61 30 26 57 7 36
36| 0 36 19 55 38 2 53 17 23 51 4 32 49 21 34 6 46 10 61 25 8 44 27 63 57 29 42 14 31 59 12 40 7 35 20 48 33 5 50 22 16 52 3 39 54 18 37 1 41 13 58 30 15 43 28 56 62 26 45 9 24 60 11 47
37| 0 37 17 52 34 7 51 22 31 58 14 43 61 24 44 9 62 27 47 10 28 57 13 40 33 4 48 21 3 38 18 55 39 2 54 19 5 32 20 49 56 29 41 12 26 63 11 46 25 60 8 45 59 30 42 15 6 35 23 50 36 1 53 16
38| 0 38 23 49 46 8 57 31 7 33 16 54 41 15 62 24 14 40 25 63 32 6 55 17 9 47 30 56 39 1 48 22 28 58 11 45 50 20 37 3 27 61 12 42 53 19 34 4 18 52 5 35 60 26 43 13 21 51 2 36 59 29 44 10
39| 0 39 21 50 42 13 63 24 15 40 26 61 37 2 48 23 30 57 11 44 52 19 33 6 17 54 4 35 59 28 46 9 60 27 41 14 22 49 3 36 51 20 38 1 25 62 12 43 34 5 55 16 8 47 29 58 45 10 56 31 7 32 18 53
40| 0 40 11 35 22 62 29 53 44 4 39 15 58 18 49 25 3 43 8 32 21 61 30 54 47 7 36 12 57 17 50 26 6 46 13 37 16 56 27 51 42 2 33 9 60 20 55 31 5 45 14 38 19 59 24 48 41 1 34 10 63 23 52 28
41| 0 41 9 32 18 59 27 50 36 13 45 4 54 31 63 22 19 58 26 51 1 40 8 33 55 30 62 23 37 12 44 5 38 15 47 6 52 29 61 20 2 43 11 34 16 57 25 48 53 28 60 21 39 14 46 7 17 56 24 49 3 42 10 35
42| 0 42 15 37 30 52 17 59 60 22 51 25 34 8 45 7 35 9 44 6 61 23 50 24 31 53 16 58 1 43 14 36 29 55 18 56 3 41 12 38 33 11 46 4 63 21 48 26 62 20 49 27 32 10 47 5 2 40 13 39 28 54 19 57
43| 0 43 13 38 26 49 23 60 52 31 57 18 46 5 35 8 51 24 62 21 41 2 36 15 7 44 10 33 29 54 16 59 61 22 48 27 39 12 42 1 9 34 4 47 19 56 30 53 14 37 3 40 20 63 25 50 58 17 55 28 32 11 45 6
44| 0 44 3 47 6 42 5 41 12 32 15 35 10 38 9 37 24 52 27 55 30 50 29 49 20 56 23 59 18 62 17 61 48 28 51 31 54 26 53 25 60 16 63 19 58 22 57 21 40 4 43 7 46 2 45 1 36 8 39 11 34 14 33 13
45| 0 45 1 44 2 47 3 46 4 41 5 40 6 43 7 42 8 37 9 36 10 39 11 38 12 33 13 32 14 35 15 34 16 61 17 60 18 63 19 62 20 57 21 56 22 59 23 58 24 53 25 52 26 55 27 54 28 49 29 48 30 51 31 50
46| 0 46 7 41 14 32 9 39 28 50 27 53 18 60 21 59 56 22 63 17 54 24 49 31 36 10 35 13 42 4 45 3 43 5 44 2 37 11 34 12 55 25 48 30 57 23 62 16 19 61 20 58 29 51 26 52 15 33 8 38 1 47 6 40
47| 0 47 5 42 10 37 15 32 20 59 17 62 30 49 27 52 40 7 45 2 34 13 39 8 60 19 57 22 54 25 51 28 11 36 14 33 1 46 4 43 31 48 26 53 21 58 16 63 35 12 38 9 41 6 44 3 55 24 50 29 61 18 56 23
48| 0 48 59 11 45 29 22 38 1 49 58 10 44 28 23 39 2 50 57 9 47 31 20 36 3 51 56 8 46 30 21 37 4 52 63 15 41 25 18 34 5 53 62 14 40 24 19 35 6 54 61 13 43 27 16 32 7 55 60 12 42 26 17 33
49| 0 49 57 8 41 24 16 33 9 56 48 1 32 17 25 40 18 35 43 26 59 10 2 51 27 42 34 19 50 3 11 58 36 21 29 44 13 60 52 5 45 28 20 37 4 53 61 12 54 7 15 62 31 46 38 23 63 14 6 55 22 39 47 30
50| 0 50 63 13 37 23 26 40 17 35 46 28 52 6 11 57 34 16 29 47 7 53 56 10 51 1 12 62 22 36 41 27 31 45 32 18 58 8 5 55 14 60 49 3 43 25 20 38 61 15 2 48 24 42 39 21 44 30 19 33 9 59 54 4
51| 0 51 61 14 33 18 28 47 25 42 36 23 56 11 5 54 50 1 15 60 19 32 46 29 43 24 22 37 10 57 55 4 63 12 2 49 30 45 35 16 38 21 27 40 7 52 58 9 13 62 48 3 44 31 17 34 20 39 41 26 53 6 8 59
52| 0 52 51 7 61 9 14 58 33 21 18 38 28 40 47 27 25 45 42 30 36 16 23 35 56 12 11 63 5 49 54 2 50 6 1 53 15 59 60 8 19 39 32 20 46 26 29 41 43 31 24 44 22 34 37 17 10 62 57 13 55 3 4 48
53| 0 53 49 4 57 12 8 61 41 28 24 45 16 37 33 20 9 60 56 13 48 5 1 52 32 21 17 36 25 44 40 29 18 39 35 22 43 30 26 47 59 14 10 63 2 55 51 6 27 46 42 31 34 23 19 38 50 7 3 54 11 62 58 15
54| 0 54 55 1 53 3 2 52 49 7 6 48 4 50 51 5 57 15 14 56 12 58 59 13 8 62 63 9 61 11 10 60 41 31 30 40 28 42 43 29 24 46 47 25 45 27 26 44 16 38 39 17 37 19 18 36 33 23 22 32 20 34 35 21
55| 0 55 53 2 49 6 4 51 57 14 12 59 8 63 61 10 41 30 28 43 24 47 45 26 16 39 37 18 33 22 20 35 9 62 60 11 56 15 13 58 48 7 5 50 1 54 52 3 32 23 21 34 17 38 36 19 25 46 44 27 40 31 29 42
56| 0 56 43 19 13 53 38 30 26 34 49 9 23 47 60 4 52 12 31 39 57 1 18 42 46 22 5 61 35 27 8 48 51 11 24 32 62 6 21 45 41 17 2 58 36 28 15 55 7 63 44 20 10 50 33 25 29 37 54 14 16 40 59 3
57| 0 57 41 16 9 48 32 25 18 43 59 2 27 34 50 11 36 29 13 52 45 20 4 61 54 15 31 38 63 6 22 47 19 42 58 3 26 35 51 10 1 56 40 17 8 49 33 24 55 14 30 39 62 7 23 46 37 28 12 53 44 21 5 60
58| 0 58 47 21 5 63 42 16 10 48 37 31 15 53 32 26 20 46 59 1 17 43 62 4 30 36 49 11 27 33 52 14 40 18 7 61 45 23 2 56 34 24 13 55 39 29 8 50 60 6 19 41 57 3 22 44 54 12 25 35 51 9 28 38
59| 0 59 45 22 1 58 44 23 2 57 47 20 3 56 46 21 4 63 41 18 5 62 40 19 6 61 43 16 7 60 42 17 8 51 37 30 9 50 36 31 10 49 39 28 11 48 38 29 12 55 33 26 13 54 32 27 14 53 35 24 15 52 34 25
60| 0 60 35 31 29 33 62 2 58 6 25 37 39 27 4 56 47 19 12 48 50 14 17 45 21 41 54 10 8 52 43 23 5 57 38 26 24 36 59 7 63 3 28 32 34 30 1 61 42 22 9 53 55 11 20 40 16 44 51 15 13 49 46 18
61| 0 61 33 28 25 36 56 5 50 15 19 46 43 22 10 55 63 2 30 35 38 27 7 58 13 48 44 17 20 41 53 8 37 24 4 57 60 1 29 32 23 42 54 11 14 51 47 18 26 39 59 6 3 62 34 31 40 21 9 52 49 12 16 45
62| 0 62 39 25 21 43 50 12 42 20 13 51 63 1 24 38 15 49 40 22 26 36 61 3 37 27 2 60 48 14 23 41 30 32 57 7 11 53 44 18 52 10 19 45 33 31 6 56 17 47 54 8 4 58 35 29 59 5 28 34 46 16 9 55
63| 0 63 37 26 17 46 52 11 34 29 7 56 51 12 22 41 31 32 58 5 14 49 43 20 61 2 24 39 44 19 9 54 62 1 27 36 47 16 10 53 28 35 57 6 13 50 40 23 33 30 4 59 48 15 21 42 3 60 38 25 18 45 55 8This time, for the inverse of a value (for a division), we find the “1” as a result of a multiplication. For example in the table above, the inverse for GF(2⁶) of 59 is 4, as 59 times 4 gives 1.
Conclusion
As in innovator, continually question things, and don’t take things for granted. The GPS service on your phone, took more than four decades of solid research to get in into a device that fits in your pocket. For this, reseachers continually question the limits of the possible.
If you are interested, here’s some material on Galois Fields: