Only 51 Have Been Found: Here’s Mersenne Primes

Only 51 Have Been Found: Here’s Mersenne Primes
And, so what’s the next number in the sequence 3, 7, 31, and 127? Well, it’s 8,191, and I will explain why in a little minute.
If you need to test with prime numbers — such as with public key encryption — how do you remember some large ones that you can test with? Well, one of the easiest ways is to remember the Mersenne prime numbers.
Mersenne prime numbers were first defined by Marin Mersenne and who was a 17th Century French Minim friar. His main contribution included his investigations of prime numbers, along with being seen as the father of acoustics. A Mersenne prime is defined as a prime number that is one less than a power of two. The general form is M_n=2^n−1 where n is an integer. The discovery of 2¹¹²¹³-1 was even given its own postmark:

The largest found is 2⁸²⁵⁸⁹⁹³³-1, and is the 51st Mersenne prime to be ever found). Since 1997, the Great Internet Mersenne Prime Search (GIMPS) distributed system has been used to find new Mersenne primes.
From Wikipedia, here are the first 20:

The Mersenne sequence becomes:
2, 3, 5, 7, 13, 17, 19, 31, 61, 89, 107, 127, 521, 607, 1279, 2203, 2281, 3217, 4253, 4423, 9689, 9941, 11213, 19937, 21701, 23209, 44497, 86243, 110503, 132049, 216091, 756839, 859433, 1257787, 1398269, 2976221, 3021377, 6972593, 13466917, 20996011, 24036583, 25964951, 30402457, 32582657, 37156667, ..., 77232917 ...Some code to discover these is [here]:
import galois
import sys
n=2
if (len(sys.argv)>1):
n=int(sys.argv[1])
print("Mersenne_exponents:", galois.mersenne_exponents(n))
print("Mersenne primes:", galois.mersenne_primes(n))and a sample run [here]:
Mersenne_exponents: [2, 3, 5, 7, 13, 17, 19, 31, 61, 89, 107, 127, 521, 607]
Mersenne primes: [3, 7, 31, 127, 8191, 131071, 524287, 2147483647,
2305843009213693951, 618970019642690137449562111,
162259276829213363391578010288127, 170141183460469231731687303715884105727,
6864797660130609714981900799081393217269435300143305409394463459185543183397656052122559640661454554977296311391480858037121987999716643812574028291115057151,
531137992816767098689588206552468627329593117727031923199444138200403559860852242739162502265229285668889329486246501015346579337652707239409519978766587351943831270835393219031728127]We can see that 2⁶⁰⁷-1 is 531137992816767098689588206552468627329593117727031923199444138200403559860852242739162502265229285668889329486246501015346579337652707239409519978766587351943831270835393219031728127.
The FourQ Curve
The core of the security you are using to access this page is probably provided with Elliptic Curve Cryptography (ECC), and where a session key is created through ECDH (Elliptic Curve Diffie Hellman). While there are a number of curves we can use, such as NIST P-256, Curve 25519 (as used in Tor) and Secp256k1 (as used with Bitcoin), there are some doubts about their security and their performance. And so Microsoft Research has produced the FourQ curve and which has 128-bit security. It is open source and runs efficiently on a number of platforms. At its core is the usage of the Mersenne prime of 2¹²⁷-1 [here]:

In tests, the Microsoft team showed that FourQ was four or five times faster than the NIST P-256 curve, and two or three times faster than Curve 25519. As so we turn to the wonderful Cloudflare, and their Circl library. Within this, Cloudflare has implemented FourQ, and is [here]:
package main
import (
"crypto/rand"
"fmt"
"io"
"encoding/hex"
"github.com/cloudflare/circl/ecc/fourq"
)
// 32 byte keys used
const Size = 32 //
type Key [Size]byte
// From secret s, calculate public key (public=aG)
func KeyGen(public, s *Key) {
var P fourq.Point
P.ScalarBaseMult((*[32]byte)(s))
P.Marshal((*[Size]byte)(public))
}
func Shared(shared, secret, public *Key) bool {
var P, Q fourq.Point
ok := P.Unmarshal((*[Size]byte)(public))
Q.ScalarMult((*[Size]byte)(secret), &P)
Q.Marshal((*[Size]byte)(shared))
ok = ok && Q.IsOnCurve()
return ok
}
func main() {
var AliceSecret, BobSecret,
AlicePublic, BobPublic,
AliceShared, BobShared Key
// Generate Alice's private key and public key
_, _ = io.ReadFull(rand.Reader, AliceSecret[:32])
KeyGen(&AlicePublic, &AliceSecret)
// Generate Bob's private key and public key
_, _ = io.ReadFull(rand.Reader, BobSecret[:])
KeyGen(&BobPublic, &BobSecret)
fmt.Println("Fourq key sharing")
fmt.Println("Alice Secret: ", hex.EncodeToString(AliceSecret[:32]))
fmt.Println("Alice Public: ",hex.EncodeToString(AlicePublic[:32]))
fmt.Println("\n\nBob Secret: ", hex.EncodeToString(BobSecret[:32]))
fmt.Println("Bob Public: ",hex.EncodeToString(BobPublic[:32]))
// Determine shared keys
Shared(&AliceShared, &AliceSecret, &BobPublic)
Shared(&BobShared, &BobSecret, &AlicePublic)
fmt.Println("\n\nBob Shared:\t", hex.EncodeToString( BobShared[:32] ))
fmt.Println("Alice Shared:\t", hex.EncodeToString( AliceShared[:32] ))
}With this, Alice produces her private key (a), and Bob produces his private key (b). We select a point on the elliptic curve (G), and Alice passes aG to Bob, and Bob passes bG to Alice. The shared key is then abG. A sample run is [here]:
== Fourq key sharing
Alice Secret: 4d4ae7584414589e7688507cbd0eb1f107352176eac219ec49d698e0868f83a6
Alice Public: 6e34b72d675cf331ed856393580e9f74fce2a9d2cce10f2e15d58070a70d2567Bob Secret: 19b5c6a97dad74f0ffdaf9cb4bec561de3124b4c90f90f2f618db6cc0f5f9b8e
Bob Public: e2159ddc2efc501ccc01f1df78d5d14061edf3b284ae98095e747b7aeac63306Bob Shared: 0112c5090679d20d4363a670ff61d554284519c6d371e61cc9526d65d5a763a0
Alice Shared: 0112c5090679d20d4363a670ff61d554284519c6d371e61cc9526d65d5a763a0And in the end Bob and Alice have the same shared key, and which they could use for a tunnel.
The Mersenne Twister
Another application of Mersenne primes is in the implementation of a random number generation and is known as the Mersenne twist. A typical exponent value used is 19,937 (2²¹⁹⁹³⁷-1). Overall, PRNGs are deterministic and periodic, but the core strength of the Twister method is the pseudo sequence is unlikely to repeat with 2¹⁹⁹³⁷-1 random numbers:

Overall the method uses sequential states, and where it should not be reasonably possible to know the next state from the current state. But some researchers have shown that “sparse” states can exist, and where there are very few ones or very few zeros, the next state will also be sparse.
The method has been criticized for using up so many bits (19,937) for the states, and that for security a state value of 256 bits would still be enough, but have a strong effect on the overall performance of the method. A pseudo sequence repeating in 2²⁵⁶ can still be seen as being secure.
If you want to try this, click [here].
Lucas-Lehmer Test
The Lucas–Lehmer test (LLT) is used to test for the primality of Mersenne numbers. It was initially created Edouard Lucas in and then enhanced by Derrick Hentry Lehmer:

For this test, we initially define u_0=0 and we calculate:
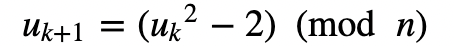
If u_{s−2}=0 then it is a prime number. Here are some tests for Mersenne Primes:
The following is the code [here]:
import sys
s=18
if (len(sys.argv)>1):
s=int(sys.argv[1])
if (s>127):
sys.exit(1)
u=4
n=pow(2,s)-1
print (f"n=2^{s}-1={n}\n")
for k in range(1,s-1):
u=((u*u)-2) %n
print (u,end=' ')
if (u==0):
print ("\n\nIt is prime")
else:
print ("\n\nIt is not prime")And a sample run for 2¹⁹-1 [here]:
n=2^19-1=52428714 194 37634 218767 510066 386344 323156 218526
504140 103469 417706 307417 382989 275842 85226 523263 0
It is primeConclusions
Great Internet Mersenne Prime Search (GIMPS) distributed system continues to try and discover the next Mersenne prime [here]. In April 2021, it stopped using the Lucas-Lehmer, and moved on to the Fermat PRobable Prime (PRP) Test. This uses:
a^{p-1} (mod p) = 1
and where p is a prime number.
If you want to discover more about the wonderful world of prime numbers, try here: