Can I Prove That I Have Used A Random Number Generator?

Can I Prove That I Have Used A Random Number Generator?
Meet Verifiable Random Functions (VRFs)
Okay, let’s say you have a lottery, and I think you are cheating. I believe that the numbers you are generating are not random. So can I get you to prove that you are truly generated random numbers? For this, we take the seed of a random number and a private key, and feed these into a hash function. With the random value, a proof and a public key, we can then prove that we have used the hash function correctly, without revealing the original seed value.
Verifiable Random Function (VRF)
Two of the greats of cryptography are Silvio Micali (creator of the Algorand blockchain) and Michael Rabin, and when they get together, magic can happen [2]:

The paper outlined how we can create a random function, of which we can prove its operation — a Verifiable Random Function (VRF). Basically, it allows us to prove that
Overall, a VRF allows the owner of a private key the ability to create a hashed value of data, while anyone with the associated public key can prove the validity of the hash. Thus the owner of the private key can produce H(x) from H(x)=f_priv(x), while someone with the public key can prove that H(x) is the hash of x. This is similar to the approach of keyed cryptography hashes but uses public-key encryption for the key operation.
A demo of the method I will outline is here:
https://asecuritysite.com/zero/vrf
For this we will use the method coded by Google and defined in the appendix of [1][here]:

Methodology
The method in the paper is defined in a discrete log format, but we now normally use elliptic curve methods. It is fairly easy to convert from a discrete log format (with exponentiation) to multiplication:
g^x → x.G
and where g is the base in the discrete log form, and G is the base point on the curve. With elliptic curves, we have two core operations: a point add, and a point scalar multiply.
With the method, initially Alice creates a random private key of x. Her public key is then:
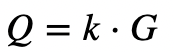
and where G is the base point on the curve. Next, she selects a random value of r, and then takes a hash of the message (m) and matches it to the curve:

Next she computers the VRF value:

This is the hash of the value x. Next, she has to create the proof of converting x in VRF, so creates a scalar value (s) using the following:

and:
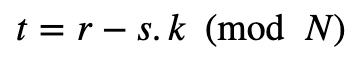
and where N is the order of the curve. The proof is then (s,t,VRF). To prove, Bob takes Alice’s public key (kG) and computes:

Next Bob computes:

Now Bob computes:

Bob then checks that h_2 is equal to s. If so, the hash has been proven.
Note that H1() hashes the data to a point on the curve, while H2() hashes to a scalar value.
Coding
We will use the code defined [here]:
package main
import (
"fmt"
"os"
"github.com/google/keytransparency/core/crypto/vrf/p256"
)
func main() {
k, pk := p256.GenerateKey()
d1 := "This is a test"
d2 := "This is not a test"
argCount := len(os.Args[1:])
if argCount > 0 {
d1 = os.Args[1]
}
if argCount > 1 {
d2 = os.Args[2]
}
m1 := []byte(d1)
m2 := []byte(d2)
index1, proof1 := k.Evaluate(m1)
index2, proof2 := k.Evaluate(m2)
fmt.Printf("== Creation of proofs ===\n")
fmt.Printf("Data: [%s] Index: %x Proof: %x\n", m1, index1, proof1)
fmt.Printf("Data: [%s] Index: %x Proof: %x\n", m2, index2, proof2)
fmt.Printf("\n== Verfication of proofs ===\n")
newindex1, _ := pk.ProofToHash(m1, proof1)
fmt.Printf("Result 1: %x\n", newindex1)
if index1 == newindex1 {
fmt.Printf("Proven\n")
}
newindex2, _ := pk.ProofToHash(m2, proof2)
fmt.Printf("Result 2: %x\n", newindex2)
if index2 == newindex2 {
fmt.Printf("Proven\n")
}
}A sample run shows that a valid encryption key produces a valid proof, and then an invalid one generates an incorrect proof:
== Creation of proofs ===
Data: [hello] Index: 071a928acd52349f74f932c183946b4a8c4d44de59a627e16d3dff2104d5f8d5 Proof: 816851f928f1ff5f15504cffa51e4be12df9ad0ccb67158718db3268d6d6ca3355ad33f888588f7e862ac8ca428e62c775b6063fc7f39751cbedde36689ce01d041173d72b619f3b5ddfe398bab6851ec5870aa29d8bc4655ef8c6a4fb8575f058be8282179f1e90eedfa9ed04837f32dde01c143826db05fcd12a93689c650dbf
Data: [hello2] Index: cbdb230c421f0f72d8d5e1c64edbb78cec6c1439448db19f414a93ccaf2f2f2f Proof: a9a7650a7c5decc9a1a10d2d854bb08a183fb3f20c641e3149b15fb55d7cc8bdc72d1ca42b41232ea6453ac186e0fe0ed9c09deedd0e56833fc4e1894567512104ad6c7761e441683e665fcafbbbe1dfa298404ae835a740ec26d72585f4ecf860993ce99512e16ef7b7abe357891f03cd04e10652d781e2dd440661adec7cd2ab== Verfication of proofs ===
Result 1: 071a928acd52349f74f932c183946b4a8c4d44de59a627e16d3dff2104d5f8d5
Proven
Result 2: cbdb230c421f0f72d8d5e1c64edbb78cec6c1439448db19f414a93ccaf2f2f2f
ProvenConclusions
Isn’t that clever? I can have a secret method that you can’t compute, but I can show you that my input and the output tally up. If you want the demo, it is here:
https://asecuritysite.com/zero/vrf
If you are interested in learning more about Zero-knowledge proofs:
https://asecuritysite.com/zero/
References
[1] Melara, M. S., Blankstein, A., Bonneau, J., Felten, E. W., & Freedman, M. J. (2015). {CONIKS}: Bringing Key Transparency to End Users. In 24th {USENIX} Security Symposium ({USENIX} Security 15) (pp. 383–398).
[2] Micali, S., Rabin, M., & Vadhan, S. (1999, October). Verifiable random functions. In 40th annual symposium on foundations of computer science (cat. №99CB37039) (pp. 120–130). IEEE.