How Does Peggy Prove Her Identity Without Giving Away the Root of Her Identity?

What’s the best way to prove our identity (or prove that you know a secret without giving it away)? Well, one of the most reliable is for…
Schnorr NI-ZKP [here]

How Does Peggy Prove Her Identity Without Giving Away the Root of Her Identity?

What’s the best way to prove our identity (or prove that you know a secret without giving it away)? Well, one of the most reliable is for you to generate a random number (x), and then store this in your digital wallet. You can then create a public value (X) when does not reveal the random value. In a discrete log form, we can represent this as:

But, these days, we do not use discrete logs, and convert this into an elliptic curve method with:

and where G is a base point on the curve, x is a scalar value, and X is a point on the curve.

Method

And, so, Peggy must prove her identity to Victor, and do it so that she does not reveal the secret of her identity (x). She can do this with a Zero Knowledge Proof (ZKP).

With the Schnorr non-interactive zero-knowledge (NIZK) proof, we can prove knowledge of a discrete logarithm without leaking its value. For example, we can prove that we know g^x (mod p) without revealing x. These days, we tend to convert our discrete log problem to elliptic curves, so let’s convert the Schnorr NIZK proof into an elliptic curve method. Initially, Peggy (the prover) defines a private key (or secret) of x, and publishes her public key:

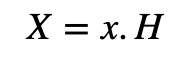
and where H is a point on the elliptic curve. Next, Peggy chooses a random value v from 1 to n−1 and where n is the order of the curve. She then computes:

This is then sent to Victor, and who creates a challenge c between 0 and 2^t−1, and where t is the bit length of the challenge. Victor then sends c to Peggy. She then computes:

Peggy will then send V and r to Victor. He then performs these verifies:

This works because:

To make this non-interactive using a random oracle model, and where Peggy generates her own value of c from:

With the non-interactive ZKP (NI-ZKP), Peggy thus creates the challenge (c), and then generates (V,r), in order to prove that she knows x. The method is then:

Schnorr NI-ZKP [here]

Coding

We can use the CIRCL library from Cloudflare to implement [here]:

package main
import (
 "crypto/rand"
 "fmt"
 "os"
 "io"
 "github.com/cloudflare/circl/group"
)

func ProveGen(myGroup group.Group, H, X group.Element, x group.Scalar, peggyID, victorID, dst []byte, rnd io.Reader) (group.Element, group.Scalar) {
 v := myGroup.RandomNonZeroScalar(rnd)
 V := myGroup.NewElement()
 V.Mul(H, v)
 // Hash  (H | V | X | peggyID | victorID) for challenge
 HByte, errByte := H.MarshalBinary()
 if errByte != nil {
  panic(errByte)
 }
 VByte, errByte := V.MarshalBinary()
 if errByte != nil {
  panic(errByte)
 }
 XByte, errByte := X.MarshalBinary()
 if errByte != nil {
  panic(errByte)
 }
 hashByte := append(HByte, VByte...)
 hashByte = append(hashByte, XByte...)
 hashByte = append(hashByte, peggyID...)
 hashByte = append(hashByte, victorID...)
 c := myGroup.HashToScalar(hashByte, dst)
 xc := myGroup.NewScalar()
 xc.Mul(c, x)
 r := v.Copy()
 r.Sub(r, xc)
 return V, r
}

func Verify(myGroup group.Group, H, X group.Element, V group.Element, r group.Scalar, peggyID, victorID, dst []byte) bool {
 HByte, errByte := H.MarshalBinary()
 if errByte != nil {
  panic(errByte)
 }
 VByte, errByte := V.MarshalBinary()
 if errByte != nil {
  panic(errByte)
 }
 RByte, errByte := X.MarshalBinary()
 if errByte != nil {
  panic(errByte)
 }
 hashByte := append(HByte, VByte...)
 hashByte = append(hashByte, RByte...)
 hashByte = append(hashByte, peggyID...)
 hashByte = append(hashByte, victorID...)
 c := myGroup.HashToScalar(hashByte, dst)
 rH := myGroup.NewElement()
 rH.Mul(H, r)
 cR := myGroup.NewElement()
 cR.Mul(X, c)
 rH.Add(rH, cR)
 return V.IsEqual(rH)
}
func main() {
 dst := "Zero"
 myGroup := group.P256
 curvetype := "P256"
 argCount := len(os.Args[1:])
 if argCount > 0 {
  curvetype = os.Args[1]
 }
 if argCount > 1 {
  dst = os.Args[2]
 }
 switch curvetype {
 case "P256":
  myGroup = group.P256
 case "P384":
  myGroup = group.P384
 case "P521":
  myGroup = group.P521
 }
 x := myGroup.RandomNonZeroScalar(rand.Reader)
 H := myGroup.RandomElement(rand.Reader)
 X := myGroup.NewElement()
 X.Mul(H, x)
 rnd := rand.Reader
 V, r := ProveGen(myGroup, H, X, x, []byte("Peggy"), []byte("Victor"), []byte(dst), rnd)
 verify := Verify(myGroup, H, X, V, r, []byte("Peggy"), []byte("Victor"), []byte(dst))
 fmt.Printf("Value to prove (x): %v\n\n", x)
 fmt.Printf("Public value (X):\n%v\n\n", X)
 fmt.Printf("Curve used: %s\n\n", curvetype)
 fmt.Printf("Domain separation: %s\n\n", dst)
 if verify == true {
  fmt.Printf("Proof (V):\n%v\n\nr: %v\n\n", V, r)
  fmt.Printf("Verify: True")
 } else {
  fmt.Printf("ZKP failed")
 }
}

A sample run [here]:

Value to prove (x): 0x9edcbf2138f1d1fcd3e0f900a743666199490c43bb4f8ec8437ef876d55ba9d7
Public value (X):
x: 0x19ca69902bfc701f4a5eea7d77d508ede846de3a4a15c0abbb70a7734ba285f9
y: 0x392687ba57e196ebdf8947d2d33ea39f23dbbffdd93a31cf3c7f5da313ea44c9
Curve used: P256
Domain separation: Hello
Proof (V):
x: 0x8feea5318bd201806756dca6cacedb5bb977c66a162e9b250fb3c94cf7bb523
y: 0x7652f2aa7f8623c0449c6fa692c04e5127c3f1ff19686a1d1213c1d99783301d
r: 0xb3c0c9560725a921872ad32f6818b480ded2af6d3bdbad337cc655ba2bd1f70d
Verify: True

Conclusions

In this case, we used a private key secret, but the secret could be a hash of any piece of data that is secret. If you are interested in ZKPs, try here:

https://asecuritysite.com/zero/

and with the CIRCL library:

https://asecuritysite.com/circl/