What Happens If I Don’t Trust The Dealer in a Card Game: A Bit of Mental Poker in a

What Happens If I Don’t Trust The Dealer in a Card Game: A Bit of Mental Poker in a Distributed World
Okay. You have 52 cards, and you have five people in the game ( Alice, Bob, Carol, Dave and Eve), and they are all remote and none of them trusts any dealer. So how can you create a game, where we shuffle the cards, and where each player will get the same card dealt as each other? One method is defined within the following paper [here]:

What we want to do, is to generate 52 encrypted cards (E(ci)), and send them to each of the players. They will then shuffle them with a randomization factor for each encrypted card, and we should still be able to prove that the shuffle is still correct. We need certain features for our game of poker. The first is that the deal is correct for all the players and that each player can confirm the correctness of the deal. The second is that an adversary will not learn anything about the cards if they are dealt face down. Finally, we need to make sure that any player dropping out, does not stop the game.
In a poker game we normally have a dealer, and who is a trusted third party (TTP). But, let’s say we do not trust any deal. For this, we can distribute trust. Also, the dealer is a single point of failure. And, can we trust the dealer to always give the cards a good shuffle? For example, the dealer may be tired and only shuffle a few times (or perhaps not at all). It is thus difficult for us to check the number of times that the dealer has shuffled the cards. But, methods of the past have shown that it can take up to eight hours to properly shuffle a pack of cards. We can also encrypt each card, and then ask each player to mix them using a secret sequence. But, this will be inefficient from a computation point of view. For five players, we require 6,099 operations to set up the shuffle:
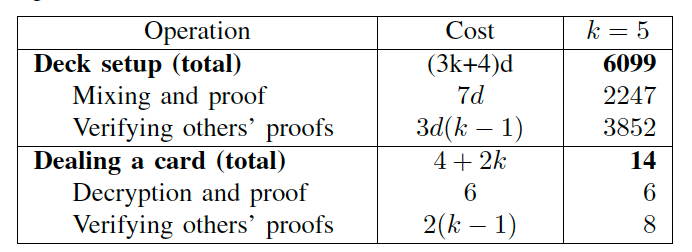
While many shuffling methods will generate all the cards, and then give them a shuffle, this method generates a random card each time, and then deal with them. To generate a card, each player computes the encryption value E(c) from a random number (c). The value of c will be between 1 and 52. If the value is the same as the one previously generated, they will all discard that card, and then generate a new one. For a face-up deal, all the players then work together to decrypt the card, and for a face-down deal, the players allow the recipient to learn the value of c.
This method is efficient if we are dealing with just a few cards, as the likelihood of duplicates will be relatively low. But, it is obviously not efficient if we use the whole deck, as there would be many duplicates.
We then need to prove that the shuffle and the re-randomization process have worked correctly. It uses the ElGamal method which has the advantage of implementing additive homomorphic encryption and also creating a shared public and private key.
The properties used are:
- Generate the encryption key E, and distribute it to all the players. Each player has the same public key and a share of the private key.
- The ElGamal property of E(m1+m2) = E(m1).E(m2)
- With E(c)=E(c’), a player can learn that c is equal to c’, without revealing c.
To deal a card, each player generates a random number (r_i) from 0 to 51, and then encrypts to get E(r_i). They also create a commitment to E(r_i). Each player then shares their encrypted value, and the encrypted cards is then multiplied to give:
E(c) = E(r_1). E(r_2) … = E(r_1+r_2…)
Thus c is the summation of the random values. The players then test the card to see if the encrypted value already exists. If it does, they discard it and regenerate. For a face-up deal, all the players can then decrypt the card E(c) and reveal c (mod 52). To deal face-down to a player (Pj), all the players compute their encrypted part without the player’s shares. Only Pj can then reveal the card.
In this case, we will create a public key and a private key for the encryption, which we will share with all of the players. We will then use this to encrypt a number of cards (“1”, “2”,…). In ElGamal, we create two values for each card: K and C.
The following is the code [uses this library here] [Sample run]:
package main
import (
"go.dedis.ch/kyber/v3"
"go.dedis.ch/kyber/v3/group/edwards25519"
"go.dedis.ch/kyber/v3/proof"
"go.dedis.ch/kyber/v3/xof/blake2xb"
"go.dedis.ch/kyber/v3/shuffle"
"fmt"
"encoding/hex"
"strconv"
"go.dedis.ch/kyber/v3/util/random"
"os"
)
func ElEncrypt(group kyber.Group, pubkey kyber.Point, message []byte) (
K, C kyber.Point, remainder []byte) {
// Embed the message (or as much of it as will fit) into a curve point.
M := group.Point().Embed(message, random.New())
max := group.Point().EmbedLen()
if max > len(message) {
max = len(message)
}
remainder = message[max:]
// ElGamal-encrypt the point to produce ciphertext (K,C).
k := group.Scalar().Pick(random.New()) // ephemeral private key
K = group.Point().Mul(k, nil) // ephemeral DH public key
S := group.Point().Mul(k, pubkey) // ephemeral DH shared secret
C = S.Add(S, M) // message blinded with secret
return
}
func ElDencrypt(group kyber.Group, prikey kyber.Scalar, K, C kyber.Point) (
message []byte, err error) {
// ElGamal-decrypt the ciphertext (K,C) to reproduce the message.
S := group.Point().Mul(prikey, K) // regenerate shared secret
M := group.Point().Sub(C, S) // use to un-blind the message
message, err = M.Data() // extract the embedded data
return
}
func main() {
var k = 4
argCount := len(os.Args[1:])
if (argCount>0) { k,_= strconv.Atoi(os.Args[1]) }
rand := blake2xb.New([]byte("Bob"))
suite := edwards25519.NewBlakeSHA256Ed25519WithRand(rand)
// suite := edwards25519.NewBlakeSHA256Ed25519WithRand(blake2xb.New(nil))
// rand := suite.RandomStream()
h := suite.Scalar().Pick(rand)
H := suite.Point().Mul(h, nil)
fmt.Printf("Private key %s\n",h)
K := make([]kyber.Point, k)
C := make([]kyber.Point, k)
fmt.Println("\n==Encrypting cards==")
for i := 0; i < k; i++ {
m := []byte(strconv.Itoa(i))
K[i], C[i], _ = ElEncrypt(suite, H, m)
fmt.Printf("[%d] K: %s, C: %s\n",i,K[i],C[i])
}
fmt.Println("\n==Check for decryption==")
fmt.Printf("Decrypted (before shuffle): ")
for i := 0; i < k; i++ {
M_decrypted, _ := ElDencrypt(suite, h, K[i], C[i])
fmt.Printf(" %s ",string(M_decrypted))
}
fmt.Println("\n\n== Shuffling and re-randomising keys==")
K2,C2, prover := shuffle.Shuffle(suite, nil, H, K, C, rand)
for i := 0; i < k; i++ {
fmt.Printf("K: %s, C: %s\n",K2[i],C2[i])
}
fmt.Println("\n\n==Check for decryption==")
fmt.Printf("Decrypted (after shuffle): ")
for i := 0; i < k; i++ {
M_decrypted, _ := ElDencrypt(suite, h, K2[i], C2[i])
fmt.Printf(" %s ",string(M_decrypted))
}
prf, _ := proof.HashProve(suite, "PairShuffle", prover)
fmt.Printf("\n\nProof: %s\n",hex.Dump(prf)[:80])
verifier := shuffle.Verifier(suite, nil, H, K, C,K2, C2)
err := proof.HashVerify(suite, "PairShuffle", verifier, prf)
if err == nil {
fmt.Printf("!!! Shuffle has been proven !!!")
}
}
A sample run is [Sample run]:
Private key b0cd72ad18c8afc610b08bd774034230ecc24d35b85e528127893edb19dda705
==Encrypting cards==
[0] K: 7a68a8371d067d514c62c2c7d7189e424911820013bb5e844ab11ab3f1064050, C: 221ee6085bc1404c6610b1af37129a6f995cdc5bcca8db368a93de21eb1788c7
[1] K: 89f0f66cd8057e777c2b1ff2d10041ec511f25b8712fa932f4d9e261cdb6b37d, C: b131f8371346a364aa8ecf627f53d3292d8c16b39d7532e26d0f4ba14a465944
[2] K: f4f1e9abb06bd229825d483967fadfbf18b4c5033c8440a9b96bee7c5609d256, C: 9acac40c05ba0fcc37b9f0794dfb4093b5b520c2896d80d08a69d65d486d033d
[3] K: 48d48535bdf1da7340436613c4c77bf001c489ea4084cf7ca9896f42f1bf8ac1, C: 49fd182a306dc5d134ca22acf2d8e5af0ff150db68b1673922ec7a42110ba065
==Check for decryption==
Decrypted (before shuffle): 0 1 2 3
== Shuffling and re-randomising keys==
K: 5e39949e8229daf798df83467ed694b5b153d4748d7c763fc803af689776d462, C: 123d0970a6973aa8d6fd2958848c0b4b7b72e00b73ff0033c9e55a442a4b5faa
K: e1c7fb5bf653b8e20dac6d8a15351774d1744414c2a8763603365ff135a3c7a1, C: ea093af4160d3202d9c42f3cfb3454774b612170bf0bbfdea1bb493d11613d93
K: 6800abd21071ea6096b190416ae615822989aac3793dc709219359fbefb4d78c, C: 1f232a25914062460f532633cb2a2d924d42a80beaae3de1caa1840cf816bb56
K: 8e29b9914b81d75b8d528ee0b07105cc9ca2673457ec54be1cd8ee8c2c0d0e6a, C: 491fecb4af64e87d1eeb00f8771363f8f07a841b87a6921ee3bcded44a7bcc7a
==Check for decryption==
Decrypted (after shuffle): 1 0 3 2
Proof:
00000000 8a 26 0d be c6 08 ec a6 22 ce 37 ed 07 92 d6 af |.&......".7.....|
00000010 b1 d7 86 31 72 a3 8e a1 bb bd 47 8f 4e 9a 2a 8d |...1r.....G.N.*.|
!!! Shuffle has been proven !!!And with 10 cards:
Private key b0cd72ad18c8afc610b08bd774034230ecc24d35b85e528127893edb19dda705
==Encrypting cards==
[0] K: d90b6458287e4865b33a453bf6dfcdd9e453fac6930676661275c966fe491020, C: 969bb9871dcf2388ca8a2e76ae93c569481f29ca549bbeef4f5545de5695518b
[1] K: d6f9d30a8dcc5b08180603ee12b8e9c4af439ab39af2816153a7e958bee9441b, C: ba0a696c9948f72aaf8de84bf06b4a0d0ef8ecef09aff2f0635025c585592490
[2] K: c625a26427a869bcf95ad49e3d0faa29095fca1d785f788aa3c78e25d9b87ba4, C: acfcf5f93dc1512b76d4ddfae9d763039c99e0eac0f1fed19a9e8fbebaff625a
[3] K: 4bf2b254de59956a079e26e6970e61f2613d2efe0e98f61a4e8fb3099ed83b2c, C: e2e25fa44dd834e8ba8014362787b67f8c5260e9f5d261ef546dd588dcf4962f
[4] K: 525d26b1e2c7a19c6c60909be3fb3825aa4fde1b253c9dae6082f571cf7fa9af, C: 2534ca50c13df677d3837c15492533074274c1591e20d23d6c81bfc61372a078
[5] K: 372d44cde77428957708dfdaee2935481f683113a046b2f24c3f8d4fa1fc79a3, C: 7a0e00cde1a8bfac9ef4235a2a781494166b7422edd0076984c3e7b93b488b5c
[6] K: 2efdf32a475be94e8f323b505bf0248a75e1ca09415863f95a846d084245c8ca, C: 87ac884fa7af74ba0d8ed156215053dbce054750f2fb59564cac1206c2dbf74e
[7] K: bee201c6e677c9cdc78ca4bd4259f5e0987bd21d926f64ca21d0ab06e9e2d6ab, C: e2b54b3e654c85d75750c7347e2d7e296e607f0dab1f85c1cdc570a0bb545be6
[8] K: e070f378bf80e8ab28580970932e3e7673bb0f6e9dedc7f41cc41737b5b06a89, C: 4eeabc68c07c0eb5558b287b58b1bd2c3f8e5434c61b37a57ef2432afb9db974
[9] K: 2253ad5124d44c5b1e844b14935c808394c321a91fffe09fea4b649ed3ab6305, C: e09dd463e601d441642f3096ea66c57d59f7cc570a7727e822bccb77eb8631c7
==Check for decryption==
Decrypted (before shuffle): 0 1 2 3 4 5 6 7 8 9
== Shuffling and re-randomising keys==
K: e7b15cb6a9579c340670aae123377732cb533629d7beab420272ce92c99720fa, C: 241ab8e3b87d963aa3bde2902d79a3a73c7fea37e7a2923801fd6ffee55a0afe
K: c0f726012673550333cf05fdd8c74662dbe4a8196cfbca65828b781091292222, C: a9bca80da759608e0107a0fc6223d5c55b92a00c831a73ef0267fa65bb63c0a4
K: 951ac9b8ebf13c05e9665c8205b4fb0ff32e79637b34d13f51fb49b1e696c010, C: 350e686e0982ba54d7b7f36c23f13ffeeae683b9355ecf364abfbfe7e91af6f2
K: bf85b458fae1c2fe8c308e94a5ab91293252ec3b699f2d41b3817323fbbb979d, C: da7fcf4e19b21ffc00d2fa00dc837405fdc6ba2ae4607ea134f82ba59ff129fb
K: f216f599a207d0bda792f8dc6f7b25ca82e3c0b47f91d7bba229453028c26351, C: 73a93221f95738240d11cc7a6799b33f55eb4d104a5e0710111ac8abfcbb8dce
K: 4130079e10a37a33ed8d06ff97748a8765e817e63e2ebe6850e5bc5be1b455dc, C: 46b65f0802c7bc7353eaae59d803b2e8407831087f38247dda2f2287d2252613
K: 8f322af916ba1b6a31ea99c541ca45d76a50d14b9a589ec9e00779c667abbb06, C: b97e72aa42f1be1e97b1fd0843885987095c76c556381012d716c93711acaa7d
K: 9de3b11b852e25ed31970b612d05ded1cff94b28a4aa68896b069c1615f47a89, C: 25913ff9c6f3c2ad63e0e7aa83a2a09052667f89e42539992539539ae03fa9c9
K: f328ffb402e63ba31ab9677dcee0a29db272d5c45a0f73840038f34040c05dea, C: 165b988d5d33e0c13f17f9f4ae1da622dc92929f909f46440d402ecb0a087433
K: 3d7781792486d7150041affe7a7b2794b9b17c52fc3c0260b2ad3518d32db2a4, C: 0dc1a84cfafc8029ec5ed0f20fbed458cac75adf7a2ccfb48867062d2acb6eb3
==Check for decryption==
Decrypted (after shuffle): 0 5 3 7 4 1 6 2 9 8
Proof:
00000000 c8 ff de 54 b0 d5 4c c6 f5 ed f9 bf 27 00 dd d3 |...T..L.....'...|
00000010 42 61 9c e8 20 07 2a a7 6e 86 ac 91 62 72 4a 28 |Ba.. .*.n...brJ(|
!!! Shuffle has been proven !!!
Conclusions
And that is trust in a distributed world, where you do not fully trust anyone or anything.