Baby Kyber Part 1: Generating the Private and Public Keys

Baby Kyber Part 1: Generating the Private and Public Keys
Juggling With Polynomials in Python
I did my first lattice cryptography lecture on Friday, and it was fun to present some of the basics of Post Quantum Cryptography (PQC). As part of this, I outlined the usage of Kyber for key exchange/public key encryption, and Dilithium for digital signatures. So, let’s take a toy example to illustrate the basic principles of Kyber. In the first part of this article we will look at the basics, and see how we use polynomial values to represent our data values.
Polynomials
In polynomial representation, we can take a data value of 1101 and represent it in polynomial powers:
x³+1.x²+0x+1 = x³+x²+1
We can then multiply, divide, add and subtract polynomial values. If you remember from school, for (2x²+1) times (x+1) we get:
(2x²+1).(x+1) = 2x³+2x²+x+1
The (mod p) operation
Obviously, if we are multiplying polynomials, the coefficients of the powers could become large, so we perform a (mod q) operation on them. Let’s take a q value of 17 and let’s say we have:
a=2x⁴+3x³+10x+3
b=3x⁵+14x³+10x+4
Then, to add (mod 17), we get:
(2x⁴+3x³+10x+3)+(3x⁵+14x³+10x+4) = 3x⁵+2x⁴+17x³+20x+7
= 3x⁵+2x⁴+3x+7 (mod 17)
To subtract (mod 17), we get:
(2x⁴+3x³+10x+3)-(3x⁵+14x³+10x+4) = -3x⁵+2x⁴-11x³-1
= 14x⁵+2x⁴+6x³+16 (mod 17)
To multiply (mod 17), we get:
(2x⁴+3x³+10x+3)∗(3x⁵+14x³+10x+4)= [… working left to reader … ] =6x⁷+9x⁶+7x⁵+3x⁴+8x³+x²+2x+12 (mod17)
For division, we will get a quotient and a remainder. With integers 19 divided by 5 gives a quotient of 3 and a remainder of 4. In cryptography, we are typically only interested in the remainder value. So we get:
(2x⁴+3x³+10x+3)∗(3x⁵+14x³+10x+4) Remainder: […working left to reader … ] =2x³+3x²+10x+3 (mod17)
We can use Python to check this:
import numpy as np
import sys
import numpy
q=17
a= [2,3,10,3] // 2x^4+3x^3+10x+3
b= [3,0,14,10,4] // 3x^5+14x^3+10x+4
print (np.poly1d(a))
print (np.poly1d(b))
r1 = np.floor( np.polyadd(a,b)) % q // Polynomial add
r2 = np.floor( np.polymul(a,b)) % q // Polynomial multiply
r3 = np.floor( np.polysub(a,b)) % q // // Polynomial subtract
r4 = np.floor( np.polydiv(a,b)[1]) % q // // Polynomial divide with remainder
print (np.poly1d(r1))
print (np.poly1d(r2))
print (np.poly1d(r3))
print (np.poly1d(r4))And then the results are:
3 2
2 x + 3 x + 10 x + 3
4 2
3 x + 14 x + 10 x + 4
4 3
3 x + 2 x + 3 x + 7
7 6 5 4 3 2
6 x + 9 x + 7 x + 3 x + 8 x + 1 x + 2 x + 12
4 3 2
14 x + 2 x + 6 x + 16
3 2
2 x + 3 x + 10 x + 3The code is:
Overall, q is the modulus for the numbers. For Kyber512, this value is 3,329.
The irreducible polynomial
The next key concept relates to the maximum power of the coefficients of the powers. If we do not constrain, the values of powers will become large. And, so, for each operation, we can divide by an irreducible polynomial (a polynomial that cannot be factored), and take the remainder of the operation. This is similar to our (mod p) operation in public key encryption (and where we divide by p each time, and take the remainder of the operation). If you want some examples:
https://asecuritysite.com/gf/poly2
An irreducible polynomial of x⁴+1, will reduce our maximum coefficient power of x³. This variable (n) is defined as the maximum degree of the used polynomials. For Kyber512, this value is 256.
In Python, we basically perform a polynomial divide. As this will create two results (the division and the remainder), we take the second returned value (using [1] to identify the second argument returned):
A1 = np.floor( np.polydiv(A1,xN_1)[1]) % qThe private key (s)
First, we start with the private key, and which is an array of polynomial values. In our case we will use:

The public key (A,t)
Next, we create a matrix of polynomials for public key (A) with:

Finally, we will introduce an error polynomial:

Now we compute:
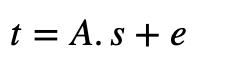
The public key is then (A,t). Using q=17, we get:


I have used this program to work this out:
# Based on https://github.com/jack4818/kyber-py
from polynomials import *
from modules import *
R = PolynomialRing(17, 4)
M = Module(R)
s0 = R([0,1,-1,1])
s1 = R([0,1,0,1])
s = M([s0,s1]).transpose()
A00 = R([11,16,16,6])
A01 = R([3,6,4,9])
A10 = R([1,10,3,5])
A11 = R([15,9,1,6])
A = M([[A00, A01],[A10, A11]])
A00 = R([1,6,16,6])
A01 = R([10,0,5,0])
A10 = R([4,5,8,3])
A11 = R([4,2,8,9])
A = M([[A00, A01],[A10, A11]])
e0 = R([1,0,1,0])
e1 = R([-1,1,0,0])
e = M([e0,e1]).transpose()
t = A @ s + e
print("s->",s)
print("e->",e)
print("A->",A)
print("t->",t)and the test run is:
s-> [x + -1*x^2 + x^3]
[ x + x^3]
e-> [1 + x^2]
[ -1 + x]
A-> [1 + 6*x + 16*x^2 + 6*x^3, 10 + 5*x^2]
[ 4 + 5*x + 8*x^2 + 3*x^3, 4 + 2*x + 8*x^2 + 9*x^3]
t-> [ 5 + 13*x + 9*x^3]
[5 + 13*x + 8*x^2 + 2*x^3]The code is here:
Our private and public key
So, we now have a private key of:

and our public key is:

and:

Overall, it is extremely difficult to derive s from A and t.
Conclusions
Watch out for Part 2, where I will encrypt and decrypt.