Baby Kyber Part 2: Encryption and Decryption

Baby Kyber Part 2: Encryption and Decryption

In the first part of this article, I showed how to generate a Kyber key pair:

Now, we will encrypt and decrypt. We will encrypt with the public key (A,t), and decrypt with the private key (s). In Kyber we modify the normal LWE (Learning With Errors) approach and use MLWE (Module Learning With Errors). With MLWE we use vectors of polynomials.

Adding errors

The first thing we need to do is to create three randomized small polynomial vectors (e_1, e_2 and r) — this must not be repeated in any future communication. In our simple example, we will use:

Converting the messaging into a polynomial

In order to process our message, we need to convert it into a polynomial. This is achieved by converting each into a coefficient. Thus “1101” becomes:

x³+x+1

Our message must then be scaled so that we have relatively large coefficients. As we have q=17, we have a halfway point of q/2, and then upscale to get a factor of 9. Our message is then:

9x³+9x+9

Encrypting

We can now take the public key (A,t) and encrypt:

and where the T symbol identifies that the matrix is transposed. The ciphertext is then u and v. In our example, the result is:

u= (12x³+ 6x²+ 3x+12 ,11x³+ 8x²+ 12x+16 )
v= (2x³ + 5x² +2)

A snippet of the code used is:

 # Based on https://github.com/jack4818/kyber-py

A,t,s=genkey()

print("A->",A)
print("t->",t)

r0 = R([0,1,-1,1]) 
r1 = R([-1,0,0,1])
r = M([r0, r1]).transpose()
    
e_10 = R([0,1,1,0])
e_11 = R([0,0,1,1])
e_1 = M([e_10, e_11]).transpose()
    
e_2 = R([0,-1,-1,-1])

m = [1,1,0,1]
poly_m = R.decode(m).decompress(1)

print("Message: ",poly_m)
    
u = A.transpose() @ r + e_1

v = (t.transpose() @ r)[0][0] + e_2 - poly_m  

print("u->",u)
print("v->",v)

Decryption

We now have the ciphertext of (u,v) and will use the private key (s) to decrypt it. This is achieved with:

This provides us with an answer which still has noise. If we expand our decryption process, we get:

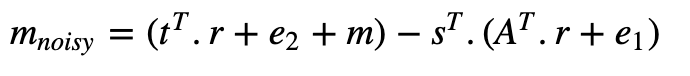
This equals:

and:

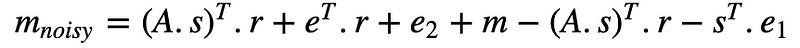
which gives:

But, we know that m is much larger than the error components (e and e2), so we can determine if the values are closer to q or 0. If they are closer to q, we define that the message bit is a 1, else it is a zero.

The code snippet for this is then:

m_n = v - (s.transpose() @ u)[0][0]

m_n_reduced = m_n.compress(1)
print("\nBefore reduced: ",m_n)
print("Decrypted: ",m_n_reduced)

Coding

Finally, here is the full coding:

 # Based on https://github.com/jack4818/kyber-py
from polynomials import *
from modules import *

R = PolynomialRing(17, 4)
M = Module(R)

def genkey():
  s0 = R([0,1,-1,1])
  s1 = R([0,1,0,1])
  s = M([s0,s1]).transpose()

  A00 = R([11,16,16,6])
  A01 = R([3,6,4,9])
  A10 = R([1,10,3,5])
  A11 = R([15,9,1,6])
  A = M([[A00, A01],[A10, A11]])

  A00 = R([1,6,16,6])
  A01 = R([10,0,5,0])
  A10 = R([4,5,8,3])
  A11 = R([4,2,8,9])
  A = M([[A00, A01],[A10, A11]])


  e0 = R([1,0,1,0])
  e1 = R([-1,1,0,0])
  e = M([e0,e1]).transpose()

  t = A @ s + e
  return A,t,s

A,t,s=genkey()

print("A->",A)
print("t->",t)

r0 = R([0,1,-1,1]) 
r1 = R([-1,0,0,1])
r = M([r0, r1]).transpose()
    
e_10 = R([0,1,1,0])
e_11 = R([0,0,1,1])
e_1 = M([e_10, e_11]).transpose()
    
e_2 = R([0,-1,-1,-1])

m = [1,1,0,1]
poly_m = R.decode(m).decompress(1)

print("Message: ",poly_m)
    
u = A.transpose() @ r + e_1

v = (t.transpose() @ r)[0][0] + e_2 - poly_m  

print("u->",u)
print("v->",v)

m_n = v - (s.transpose() @ u)[0][0]

m_n_reduced = m_n.compress(1)
print("\nBefore reduced: ",m_n)
print("Decrypted: ",m_n_reduced)

and a sample run:

A-> [1 + 6*x + 16*x^2 + 6*x^3,              10 + 5*x^2]
[ 4 + 5*x + 8*x^2 + 3*x^3, 4 + 2*x + 8*x^2 + 9*x^3]

t-> [        5 + 13*x + 9*x^3]
[5 + 13*x + 8*x^2 + 2*x^3]

Message:  9 + 9*x + 9*x^3

u-> [12 + 13*x + 6*x^2 + 12*x^3]
[16 + 12*x + 8*x^2 + 11*x^3]
v-> 2 + 5*x^2 + 2*x^3

Message:  1 + x + x^3
Decrypted:  1 + x + x^3

The code is here:

Conclusions

And there you go. A Post Quantum Cryptography method that aims to replace both ECDH (for key exchange) and RSA (for public key encryption).

So here is the full code:

https://asecuritysite.com/pqc/kyber01

References

[1] Giacomo Pope, CRYSTALS-Kyber Python Implementation, [here].

[2] Ruben Gonzalez, Kyber — How does it work?, Approachable Cryptography [here].