Thank Diophantus and Mordell For Your Online Security

And Neal Koblitz and Victor Miller, of course
Louis Mordell and Diophantus

Thank Diophantus and Mordell For Your Online Security

And Neal Koblitz and Victor Miller, of course

We perhaps increasingly live in a soulless world of AI chatbots. It’s a world that lacks any real human interaction, human invention or human spirit. It basically started with Wikipedia, and where we get instant answers to what questions we pose and without all the need for learning in between. It’s soulless place, and where we gain instant access to the knowledge we need. We are becoming a slave to the machine — and that machine is the Internet.

Overall, we are cheating ourselves, and given the current rate of progress, we will become will hold only the most basic of knowledge in our brains, and will hand over the thing that had advanced our society: our gathering of knowledge; our making sense of our complex world; and of our invention based on new thought based science. Perhaps we will gather around people in the future, who will tell stories of how they read scientific papers and wonder at their ability to discover new things without the use of AI.

And, perhaps these stories will tell tales of how the discovery of new methods changed the course of history. Unfortunately, we have become a consumer of technology, and care little about what happens underneath, and of the decades and centuries of work that has taken us to where we are. And, so, as you read this article, underneath you will find that elliptic curves are protecting you against people who wish to spy on your every access to the Internet. The magic is a very simple little maths method: the humble elliptic curve.

From Mordell to Diophantus — and back

Recently, I stumbled upon this paper [1]:

And, so as I work in elliptic curve cryptography (ECC), I was drawn to who Diophantus and Mordell were. The former — Diophantus — is easy to trace, and was a Greek mathematician who wrote a series of books on solving algebraic equations named Arithmetica.

Diophantus of Alexandria

To mathematicians, he is known for areas of number theory such as Diophantine equations and Diophantine approximations. His work involved solving equations with rational numbers (eg 3/5) which give integer solutions. For example, if we have:

x=x/3 + 2x/10 + 5

what is x? I know this will bring you out in a cold sweat as you remember those pesky rational numbers from school. If you’re interested the answer is 8, 9, and 10. For this, we get fractions in the equation which can create integer solutions:

for x in range(1,10000):
 v=x//3+2*x//10+5
 if (v==x): print("Found: ",v)

Diophantine’s work focused on finding integer solutions. For Louis Mordell, Diophatine’s work provided endless adventure, such as examing the equation of y²-k=x³ [2]:

And, if you didn’t notice, this equation is an elliptic curve, which we normally write as:

y²=x³+k

Overall, this beautiful equation is at the core of trust and security on the Internet. We make it discrete, but, at its core, it is the equation that is protecting someone from spying on your online. And, so, it was in 1914 that Louis published his work on finding solutions to these magical equations. He thus proposed how we could discover the true number of integer points that lay on the curve. For example, with y²=x³+17, we can discover that one solution is (2,5), as:

5² = 2³+17

and we get 25 on both sides. But, what other points are possible?

Mordell curve

In the elliptic cryptography field we use a finite field and use a form of:

y² = x³ + a.x + b (mod p)

The Mordell curve does not constrain the computation into a finite field and has the form of:

y² = x³ + n

The Mordell Curve comes from Louis Mordell and who showed that there are only a finite number of integer solutions to this. The bit of the paper that stuck out for me is:

So where does the 16 come from? Well, if we plot the Mordell curve for y²=x³+17, we get this [here]:

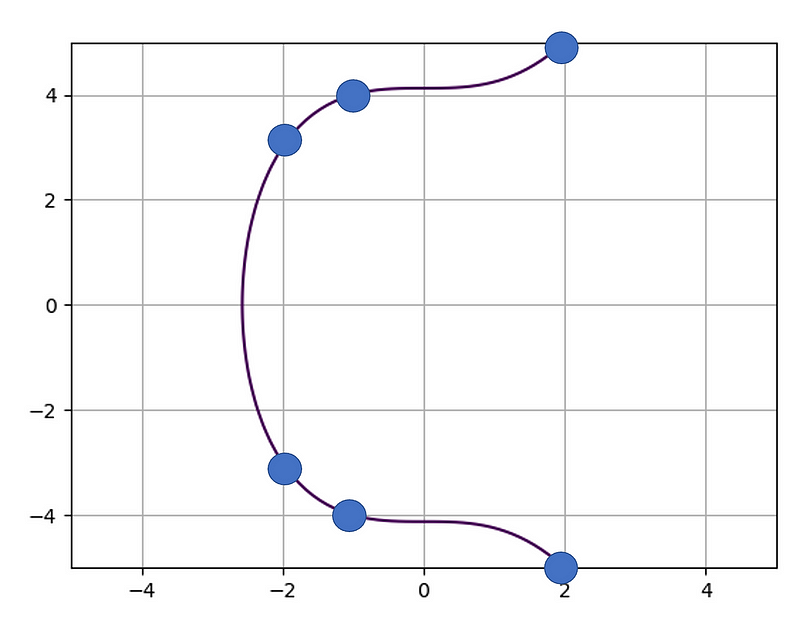
y²=x³ + 17 [here]

In this case, we can see that we have six possible points in the range of -2 to 2. In a finite field problem, we would normally be constrained with a prime number, where we find the quadratic root. But, we are not constrained, so we will have to search manually. With this, we will compute the solutions for values up to 100,000 [here]:

import math
r=100000
for x in range(-2, r):
    y_2 = x**3 + 17
    if (y_2>0):
        y=math.sqrt(y_2)
# y^2 = x^3 + 17
        if (y.is_integer()):
            print ("Found: ",int (x),int(y))

A run of this shows [here]:

Found:  -2 3
Found:  -1 4
Found:  2 5
Found:  4 9
Found:  8 23
Found:  43 282
Found:  52 375
Found:  5234 378661

And we can see we have eight points of (-2,3), (-1,4), (2,5), (4,9), (8,23), (43, 282), (52,375) and (5234,378661). Then we can add the negative values of y to get the rest of the points: (-2,-3), (-1,-4), (2,-5), (4,-9), (8,-23), (43, -282), (52,-375) and (5234,-378661). If we sample a few we get:

For (-2,-3) → (-3)² = (-2)³ + 17 -> 9 = 9
For (43,282) -> (282)² = (43)³ + 17 -> 79524 = 79507 + 17

We can try different values in n:

  • n=−2,y²=x³−2 Try
  • n=8,y²=x³+8 Try
  • n=9,y²=x³+9 Try
  • n=15,y²=x³+15 Try
  • n=17,y²=x³+17 Try
  • n=24,y²=x³+24 Try

For n=8, we get:

y^2=x^3+8
Solutions: 
Found:  1 3
Found:  2 4
Found:  46 312

Finite field elliptic curves

We don’t use Mordell curves for elliptic curve cryptography. For this, we use a finite field of the form:

y² = x³ + ax +b (mod p)

and where p is a large prime number (normally around 256 bits long). If we try a=0, b=17 and p=2²⁵⁵-19, we have:

y² = x³ + 17 (mod 2²⁵⁵-19)

Now we can use a quadratic residue method to determine the solution of (x,y) [here]:

import libnum
import sys
p=2**255-19
r=100
n=17
if (len(sys.argv)>1):
    n=int(sys.argv[1])
if (len(sys.argv)>2):
    p=int(sys.argv[2])
print(f"y^2=x^3+{n} (mod {p})\n")
for x in range(0, r):
    if (x>p): break
    y_2 = pow(x,3,p) + n
if (libnum.has_sqrtmod(y_2,{p:1})):
        y=next(libnum.sqrtmod(y_2,{p:1}))
        print (f"Found: ({x},{y})")

A sample run for the points up to x=100 is [here]:

Found:  2 5
Found:  4 9
Found:  5 57800787394070956223430301608988389592958150720113516802481917179795121371783
Found:  6 13554660953088752976062579461958686215471337427385637654648525103553495795318
Found:  8 57896044618658097711785492504343953926634992332820282019728792003956564819926
Found:  10 47422998955828599794015002653885857561096684236460224366449083273632902735987
Found:  16 5796627366330822776314552130245125238336366538586038196974127523584347737757
Found:  18 7477197912595169125689841906741303366755775410211592176225125225618836449680
Found:  21 9373982022246925351704465776923140866149779456288399414433762808823791841329
Found:  23 34363427189385326838946870757664243422073398808942794773362454787598790323870
Found:  24 42545237888504474096599642362363745805293665667123865974773547237579204451701
Found:  27 25824744157624968251761207926300702981328024388036202677891747147289191588256
Found:  29 40049969268298181298325883112532978546585056893299156654425725834432582076272
Found:  31 23816130128998847322058381740966803868843090904842359313626313702976064590975
Found:  34 24841320630278285857553940559428697998572081150684518179182261258428892177467
Found:  35 31158340905102131809307996575399725138091300555104946410051579599356257871945
Found:  37 40812849727134136473740581020366670695051299873314350606255140785275532775405
Found:  38 32934558212773578017674674077349416047723548180275295811239354111305374728678
Found:  40 26722548616731531116253010698086663312512725483801945843795048165407120129233
Found:  41 37672780910489767151961792740944799934927503581355081277863764162457061807294
Found:  42 7816688925062250952379300010221117975143960932597678495817737746030020850834
Found:  43 282
Found:  47 4399884030186173224146747235408361114530573133727980415601784090900691026741
Found:  48 26815023295711448867901192296619593590111719494569920178571836010430301683491
Found:  49 23490464128453720982333933518243484145111207249113919321404201765020796581121
Found:  52 375
Found:  53 4798588938186369510385990275250967211815701045055784882281771565712744034515
Found:  55 37809194884583519049424944536422728109816410699695581216744272897252580748167
Found:  56 55331474097510291481920787212273895378892077489276009454548782416950074368845
Found:  58 16601280762178864470815693345821597254293644920499417442666882032052386414331
Found:  61 35986750229327926102012956552408297800094277027400097866459671822092055941532
Found:  62 24353352799656889538358502288935973359020732549120591841867573126555253060451
Found:  63 30465148096954868768166528783278296895820518956946052925078883719598026460034
Found:  66 26911308819090969753859581315167042326075006111265199628340167342258977409885
Found:  70 17763050496603892639993786637998581788432052343587356690162560888647831859059
Found:  76 9917293782433180655207042834065241735321299874267850509559125693424140388114
Found:  79 53790033746405713018203233008649201092678580501330968152742712468094203274236
Found:  81 52306181368836376530513681226438934946629112112226793976253827896073414854496
Found:  83 54145057902203407050660115549725422153075727446973577296927435380661486596015
Found:  85 37184163763180592028350692802335037406647601407009365145789536944379723733320
Found:  88 46605087641559515616540059118391678318077234607015134634118152401233721721979
Found:  90 15764804636583225799885526346458760241861965824556828079076491710038558831470
Found:  91 355450063868251267908332451452511479478005565994827226364721107391238320478
Found:  92 34220996760012620671498981307164974770473670307262022939012385622503307828490
Found:  94 43366191004735476486953376934987613803964067451207958424425949246610427079817
Found:  97 11039914837507245940833514018359653337597712174101912846793001131788293318612
Found:  99 39275862361156359764865193328419687144795077692475579141197026214448912997069

Now, we see we have many more points, and where x=1, x=3 and x=93 do not exist for a solution. It should be noted that there are two y-axis points for every x-value.

Conclusions

Our online security is highly dependent on elliptic curve methods, so thank them for knowing that you have a secure encryption tunnel when connecting to Web sites. Under the hood, we use ECDH (Elliptic Curve Diffie Hellman) and which often uses the P256 curve. For Bitcoin, we use:

y²=x³ + 7 (mod p)

Here is a pure Mordell Curve:

https://asecuritysite.com/ecc/mor

And here is an example for variable values of n and p (as we would in ECC):

https://asecuritysite.com/principles/mor2

And it was Neal Koblitz and Victor Miller who eventually discovered that these magical elliptic curves could actually be used to protect our online world:

Koblitz and Miller Built The Foundation of Security For Our Internet
Your on-line security depends fundamentally on a beautiful little curve: an elliptic curve. It has been a savour for…medium.com

Perhaps, just once in a lifetime, we have the chance to change the world. In a world of ChatGPT, we hand over our greatness to the machine, and there can only be one result — a world devoid of human learning.

References

[1] Brown, E., & Myers, B. T. (2002). Elliptic curves from Mordell to Diophantus and back. The American mathematical monthly, 109(7), 639–649.

[2] Gauthier, S., & Lê, F. (2019). On the youthful writings of Louis J. Mordell on the Diophantine equation y^ 2-k= x^ 3 y 2-k= x 3. Archive for History of Exact Sciences, 73, 427–468.