Four Basic Rules of ECDSA Signatures …
Four Basic Rules of ECDSA Signatures …
In 1999, Don Johnson Alfred Menezes (1999) published a classic paper on “The Elliptic Curve Digital Signature Algorithm (ECDSA)”:

Basically, it took the DSA (Digital Signature Algorithm) — created by David W. Kravitz — and converted it into an elliptic curve representation. And, so, as discrete logs were becoming larger, elliptic curve methods were so much more efficient.
Then, in 2007, Satoshi Nakamoto started writing code for his/her Bitcoin implementation, and selected ECDSA as the main signature method, and used the secp256k1 curve. For Ethereum, too, the natural approach to use was the ECDSA signature method. But, ECDSA signatures have been prone to attack if not implemented correctly, so let’s have a look at four basic rules.
The true magic of ECDSA was that we did not have to store the public key, but where the signature could be checked from a hashed version of the private key. In this way, blockchain did not need to store the public keys of those who used it, and it was one of the first times we created a truly decentralized information infrastructure.
If you want to understand how ECDSA signatures work, try here.
Never Leak The Nonce
Example: Crack ECDSA from leak of nonce (SECP256k1). ECDSA with nonce. This outlines ECDSA how the private key can be recovered with a leak of the nonce value for SECP256k1.
With an ECDSA signature, we sign a message with a private key (priv) and prove the signature with the public key (pub). A random value (a nonce) is then used to randomize the signature. Each time we sign, we create a random nonce value and it will produce a different (but verifiable) signature. Overall the signer only has to reveal the elements of the signature and their public key, and not the nonce value. If the signer reveals just one nonce value by mistake, an intruder can discover the private key. In this case we will reveal the nonce value, and determine the private key, and use the secp256k1 curve (as used with Bitcoin).
In ECDSA, Bob creates a random private key (priv), and then a public key from:
pub=priv×G
Next, in order to create a signature for a message of M, he creates a random number (k) and generates the signature of:
r=k⋅G
s=k^{−1}(H(M)+r⋅priv)
The signature is then (r,s) and where r is the x-co-ordinate of the point kG. H(M) is the SHA-256 hash of the message (M), and converted into an integer value. If the k value is revealed for any of the signatures, an intruder can determine the private key using:
priv=r^{−1}×((k⋅s)−H(M))
This works because:
s⋅k=H(M)+r⋅priv
and so:
r⋅priv=s⋅k−H(M)
and for priv:
priv=r−1(s⋅k−H(M))
Here is some code which does a discovery of the private key, if the nonce (k) is revealed [here]:
import ecdsa
import random
import libnum
import hashlib
import sys
G = ecdsa.SECP256k1.generator
order = G.order()
print ("Curve detail")
print (G.curve())
print ("Order:",order)
print ("Gx:",G.x())
print ("Gy:",G.y())
priv = random.randrange(1,order)
Public_key = ecdsa.ecdsa.Public_key(G, G * priv)
Private_key = ecdsa.ecdsa.Private_key(Public_key, priv)
k1 = random.randrange(1, 2**127)
msg1="Hello"
if (len(sys.argv)>1):
msg1=(sys.argv[1])
m1 = int(hashlib.sha256(msg1.encode()).hexdigest(),base=16)
sig1 = Private_key.sign(m1, k1)
print ("\nMessage 1: ",msg1)
print ("Sig 1 r,s: ",sig1.r,sig1.s)
r1_inv = libnum.invmod(sig1.r, order)
s1 = sig1.s
try_private_key = (r1_inv * ((k1 * s1) - m1)) % order
print ()
print ("Found Key: ",try_private_key)
print ()
print ("Key: ",priv)
if (ecdsa.ecdsa.Public_key(G, G * try_private_key) == Public_key):
print("\nThe private key has been found")
print (try_private_key)A sample run is [here]:
Curve detail
CurveFp(p=115792089237316195423570985008687907853269984665640564039457584007908834671663, a=0, b=7, h=1)
Order: 115792089237316195423570985008687907852837564279074904382605163141518161494337
Gx: 55066263022277343669578718895168534326250603453777594175500187360389116729240
Gy: 32670510020758816978083085130507043184471273380659243275938904335757337482424
Message 1: hello
Sig 1 r,s: 31110256322898237264490243973699731757547476866639597679936653478826981616940 39826373609221276498318363598911660764943881869513002749160966300292770474312
Found Key: 95525957745036960168874600860927089941985475618074755510253043724286299804190
Key: 95525957745036960168874600860927089941985475618074755510253043724286299804190
The private key has been found
95525957745036960168874600860927089941985475618074755510253043724286299804190Beware of Weak Nonces
Example: Crack ECDSA with weak nonces (sepc256k1). ECDSA: Revealing the private key from same nonce. This outlines ECDSA how the private key can be recovered with weak nonce values.
With an ECDSA signature, we sign a message with a private key (priv) and prove the signature with the public key (pub). A random value (a nonce) is then used to randomize the signature. Each time we sign, we create a random nonce value and it will produce a different (but verifiable) signature. The private key, though, can be discovered if Alice signs two different messages with the same nonce [1].
In ECDSA, Bob creates a random private key (priv), and then a public key from:
pub=priv×G
Next, in order to create a signature for a message of M, he creates a random number (k) and generates the signature of:
r=k⋅G
s=k^{−1}(H(M)+r⋅priv)
The signature is then (r,s) and where r is the x-co-ordinate of the point kG. H(M) is the SHA-256 hash of the message (M), and converted into an integer value.
Now let’s say we have two messages (m1 and m2) and have hashes of:
h1=H(m1)
h2=H(m2)
Now let’s say that Alice signs the messages with the same private key (priv) and the same nonce (k), we can then recover the private key with:

We can also recover the nonce with:

Here is some code that does a discovery of the private key, and the nonce (k) if we use the same nonce value [here]:
import ecdsa
import random
import libnum
import hashlib
import sys
G = ecdsa.SECP256k1.generator
order = G.order()
priv1 = random.randrange(1,order)
Public_key = ecdsa.ecdsa.Public_key(G, G * priv1)
x1 = ecdsa.ecdsa.Private_key(Public_key, priv1)
k = random.randrange(1, 2**127)
msg1="Hello"
msg2="Hello1"
if (len(sys.argv)>1):
msg1=(sys.argv[1])
if (len(sys.argv)>2):
msg2=(sys.argv[2])
h1 = int(hashlib.sha256(msg1.encode()).hexdigest(),base=16)
h2 = int(hashlib.sha256(msg2.encode()).hexdigest(),base=16)
sig1 = x1.sign(h1, k)
sig2 = x1.sign(h2, k)
r1,s1 = sig1.r,sig1.s
r2,s2 = sig2.r,sig2.s
valinv = libnum.invmod( r1*(s1-s2),order)
x1rec = ( (s2*h1-s1*h2) * (valinv)) % order
print ("Message 1: ",msg1)
print (f"Signature r={r1}, s={s1}")
print ("\nMessage 2: ",msg2)
print (f"Signature r={r2}, s={s2}")
print ("\nPrivate key",priv1)
print ("\nPrivate recovered ",x1rec)
valinv = libnum.invmod( (s1-s2),order)
k1rec = ( (h1-h2) * valinv) % order
print ("\nK: ",k)
print ("\nK recovered ",k1rec)
A sample run is [here]:
Message 1: hello
Signature r=16163824871702315365636544754327339671279830383115616072776286071644348532176, s=78942102071383249892109282228339664393041099900407940222266026023142592864884
Message 2: hello1
Signature r=16163824871702315365636544754327339671279830383115616072776286071644348532176, s=83502523167965149244641473202679268630845178075816922294718909855670078364206
Private key 6542179820561127199468453109220159836323733777364616770035873205004743487369
Private recovered 6542179820561127199468453109220159836323733777364616770035873205004743487369
K: 109308891778201478280270581205739604663
K recovered 109308891778201478280270581205739604663Do Not Share Nonce Values
Example: Revealing the private key, from two keys and shared nonces (SECP256k1). ECDSA: Revealing the private key, from two keys and shared nonces (SECP256k1). This outlines ECDSA how we can reveal two private keys from four signed messages.
With an ECDSA signature, we sign a message with a private key (priv) and prove the signature with the public key (pub). A random value (a nonce) is then used to randomize the signature. Each time we sign, we create a random nonce value and it will produce a different (but verifiable) signature. The private key, though, can be discovered if Alice signs four messages with two keys and two nonces [2]. In this case, she will sign message 1 with the first private key (x1), sign message 2 with a second private key (x2), sign message 3 with the first private key (x1) and sign message 4 with the second private key (x2) The same nonce (k1) is used in the signing for messages 1 and 2, and another nonce (k2) is used in the signing of messages 3 and 4.
In ECDSA, Bob creates a random private key (priv), and then a public key from:
pub=priv×G
Next, in order to create a signature for a message of M, he creates a random number (k) and generates the signature of:
r=k⋅G
s=k−1(H(M)+r⋅priv)
The signature is then (r,s) and where r is the x-co-ordinate of the point kG. H(M) is the SHA-256 hash of the message (M), and converted into an integer value.
In this case, Alice will have two key pairs, and with two private keys (x1 and x2). She will sign message 1 (m1) with the first private key (x1), sign message 2 (m2) with a second private key (x2), sign message 3 (m3) with the first private key (x1), and sign message 4 (m4) with the second private key (x2). The same nonce (k1) is used in the signing of messages 1 and 2, and another nonce (k2) is used in the signing of messages 3 and 4. Now let’s say we have four messages (m1 .. m4) and have hashes of:
h1=H(m1)
h2=H(m2)
h3=H(m3)
h4=H(m4)
The signatures for the messages will then be (s1,r1), (s2,r1), (s3,r2), and (s4,r2):
s1=k1−1(h1+r1⋅x1)(modp)
s2=k1−1(h2+r1⋅x2)(modp)
s3=k2−1(h3+r2⋅x1)(modp)
s4=k2−1(h4+r2⋅x2)(modp)
Using Gaussian elimination, we can also recover the private keys with:

and:

Here is some code that discovers the private keys [here]:
import ecdsa
import random
import libnum
import hashlib
import sys
G = ecdsa.SECP256k1.generator
order = G.order()
priv1 = random.randrange(1,order)
Public_key = ecdsa.ecdsa.Public_key(G, G * priv1)
x1 = ecdsa.ecdsa.Private_key(Public_key, priv1)
priv2 = random.randrange(1,order)
Public_key2 = ecdsa.ecdsa.Public_key(G, G * priv2)
x2 = ecdsa.ecdsa.Private_key(Public_key2, priv2)
k1 = random.randrange(1, 2**127)
k2 = random.randrange(1, 2**127)
msg1="Hello"
msg2="Hello1"
msg3="Hello3"
msg4="Hello4"
if (len(sys.argv)>1):
msg1=(sys.argv[1])
if (len(sys.argv)>2):
msg2=(sys.argv[2])
if (len(sys.argv)>3):
msg3=(sys.argv[3])
if (len(sys.argv)>4):
msg4=(sys.argv[4])
h1 = int(hashlib.sha256(msg1.encode()).hexdigest(),base=16)
h2 = int(hashlib.sha256(msg2.encode()).hexdigest(),base=16)
h3 = int(hashlib.sha256(msg3.encode()).hexdigest(),base=16)
h4 = int(hashlib.sha256(msg4.encode()).hexdigest(),base=16)
sig1 = x1.sign(h1, k1)
sig2 = x2.sign(h2, k1)
sig3 = x1.sign(h3, k2)
sig4 = x2.sign(h4, k2)
r1,s1 = sig1.r,sig1.s
r1_1,s2 = sig2.r,sig2.s
r2,s3 = sig3.r,sig3.s
r2_1,s4 = sig4.r,sig4.s
valinv = libnum.invmod( r1*r2*(s1*s4-s2*s3),order)
x1rec = ((h1*r2*s2*s3-h2*r2*s1*s3-h3*r1*s1*s4+h4*r1*s1*s3 ) * valinv) % order
x2rec = ((h1*r2*s2*s4-h2*r2*s1*s4-h3*r1*s2*s4+h4*r1*s2*s3 ) * valinv) % order
print ("Message 1: ",msg1)
print (f"Signature r={r1}, s={s1}")
print ("\nMessage 2: ",msg2)
print (f"Signature r={r1_1}, s={s2}")
print ("\nMessage 3: ",msg3)
print (f"Signature r={r2}, s={s3}")
print ("\nMessage 4: ",msg4)
print (f"Signature r={r2_1}, s={s4}")
print ("\nPrivate key (x1):",priv1)
print ("\nPrivate recovered (x1): ",x1rec)
print ("\nPrivate key (x2):",priv2)
print ("\nPrivate recovered (x2):",x2rec)A sample run is [here]:
Message 1: hello
Signature r=96094994597103916506348675161520648758285225187589783433159767384063221853577, s=11930786632149881397940019723063699895405239832076777367931993614016265847425
Message 2: hello1
Signature r=96094994597103916506348675161520648758285225187589783433159767384063221853577, s=86716405197525298580208026914311340731533780839926210284720464080897845438167
Message 3: hello2
Signature r=12047241901687561506156261203581292367663176900884185151523104379030284412704, s=42453302255950972549884862083375617752595228510622859389343928824741407916152
Message 4: hello3
Signature r=12047241901687561506156261203581292367663176900884185151523104379030284412704, s=64279036158699242111613174757286438038132181593159757823380636958768174455517
Private key (x1): 82160419381684073393977402015108188969157550419795710258656483526045067388858
Private recovered (x1): 82160419381684073393977402015108188969157550419795710258656483526045067388858
Private key (x2): 114347697544140976184770951847100304992433696701232754239964044576164337336942
Private recovered (x2): 114347697544140976184770951847100304992433696701232754239964044576164337336942Beware of Faults
Example: Fault Attack. ECDSA: Fault Attack. In the fault attack in ECDSA we only require two signatures. One is produced without a fault (r,s), and the other has a fault (rf,sf). From these we can generate the private key.
In the fault attack in ECDSA we only require two signatures. One is produced without a fault (r,s), and the other has a fault (rf,sf). From these, we can generate the private key [3,4].
In ECDSA, Bob creates a random private key (priv), and then a public key from:
pub=priv×G
Next, in order to create a signature for a message of M, he creates a random number (k) and generates the signature of:
r=k⋅G
s=k^{−1}(h+r⋅d)
and where d is the private key and h=H(M) The signature is then (r,s) and where r is the x-co-ordinate of the point kG. h is the SHA-256 hash of the message (M), and converted into an integer value.
Now, let’s say we have two signatures. One has a fault and the other one is valid. We then have (r,s) for the valid one, and (rf,sf) for the fault. These will be:
sf=k^{−1}.(h+d.rf)(modp)
s=k^{−1}.(h+d.r)(modp)
and where h
is the hash of the message. Now if we subtract the two s
values we get:
s−sf=k^{−1}.(h+d.r)−k^{−1}.(h+d.rf)
Then:

This can then be substituted in :
s=k^{−1}(h+r.d)(modp)
This gives:
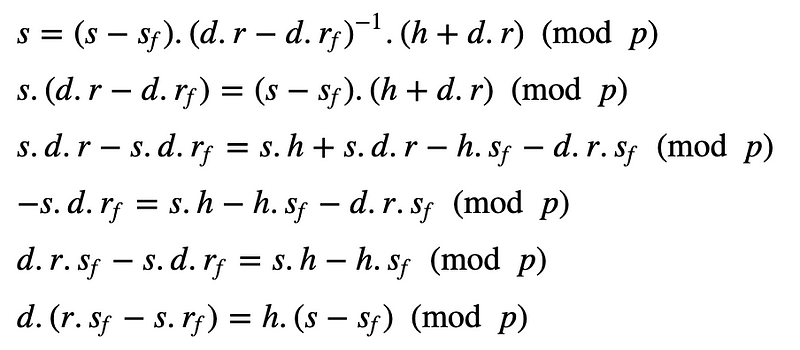
We can then rearrange this to derive the private key (d) from:

Here is the code to implement this [here]:
import ecdsa
import random
import libnum
import hashlib
import sys
G = ecdsa.SECP256k1.generator
order = G.order()
priv1 = random.randrange(1,order)
Public_key = ecdsa.ecdsa.Public_key(G, G * priv1)
d = ecdsa.ecdsa.Private_key(Public_key, priv1)
k = random.randrange(1, 2**127)
msg="Hello"
if (len(sys.argv)>1):
msg=(sys.argv[1])
h = int(hashlib.sha256(msg.encode()).hexdigest(),base=16)
sig = d.sign(h, k)
r,s = sig.r,sig.s
# Now generate a fault
rf = sig.r+1
sf=(libnum.invmod(k,order)*(h+priv1*rf)) % order
k = h*(s-sf) * libnum.invmod(sf*r-s*rf,order)
valinv = libnum.invmod( (sf*r-s*rf),order)
dx =(h*(s-sf)* valinv) % order
print(f"Message: {msg}")
print(f"k: {k}")
print(f"Sig 1 (Good): r={r}, s={s}")
print(f"Sig 2 (Faulty): r={rf}, s={sf}")
print (f"\nGenerated private key: {priv1}")
print (f"\nRecovered private key: {dx}")A sample run is [here]:
Message: hello
k: 15613459045461464441268016329920647751876410646419944753875923461028663912505625338208127533545920850138128660754322530221814353295370007218638086487275174473446354362246611811506735710487039390917643920660108528521515014507889120
Sig 1 (Good): r=84456595696494933440514821180730426741490222897895228578549018195243892414625, s=68818602365739991134541263302679449117335025608295087929401907013433000993001
Sig 2 (Faulty): r=84456595696494933440514821180730426741490222897895228578549018195243892414626, s=58598513613070973829759520121438538694005185742306423466103492198584643742545
Generated private key: 15195234419506006831576867959209365250058907799872905479943949602323611654898
Recovered private key: 15195234419506006831576867959209365250058907799872905479943949602323611654898Conclusions
ECDSA is great, but needs to be handled with care!
References
[1] Brengel, M., & Rossow, C. (2018, September). Identifying key leakage of bitcoin users. In International Symposium on Research in Attacks, Intrusions, and Defenses (pp. 623–643). Springer, Cham [here].
[2] Brengel, M., & Rossow, C. (2018, September). Identifying key leakage of bitcoin users. In International Symposium on Research in Attacks, Intrusions, and Defenses (pp. 623–643). Springer, Cham [here].
[3] Sullivan, G. A., Sippe, J., Heninger, N., & Wustrow, E. (2022). Open to a fault: On the passive compromise of {TLS} keys via transient errors. In 31st USENIX Security Symposium (USENIX Security 22) (pp. 233–250).
[4] Poddebniak, D., Somorovsky, J., Schinzel, S., Lochter, M., & Rösler, P. (2018, April). Attacking deterministic signature schemes using fault attacks. In 2018 IEEE European Symposium on Security and Privacy (EuroS&P) (pp. 338–352). IEEE.