Proof of Square Free For Paillier

Proof of Square Free For Paillier
Can I prove to you that the number that I have is not a square? For example, is the following a square?
97504752120211702535358191195648945688474873538034852939569251156352023212
14210816463913292449986057542004710628895820697964563893054228622821312108
828249Well, it is, because it is the square of this value:
98744494590945019700641753304103338870597180573220135657414878147665192918693But, why might this be important? Well in Paillier we pick two large prime numbers (p and q)). We then calculate a modulus (N=p.q) and ϕ(N)=(p−1).(q−1). We then make sure that gcd(p.q,ϕ(N))=1. A core part of Paillier is to make sure that N is not a square.
Luckily, there’s a great paper which defines the proofs required for modulus values [1][here]:

In Section 3.2, we have a proof for Paillier and the check for a square-free modulus value (N) [1][here]:

Now Victor wants Peggy to prove that the modulus is square-free. For the proof Peggy computes:

In an interactive proof, Victor (the verifier) then generates a random values as a challenge (\(x)), and passes this to Peggy. She then computes:

Peggy passes this back to Victor and Victor then checks that:
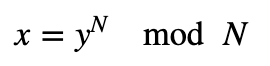
If this equals the value that was send, Peggy has proven that the modulus is square-free, as she should not be able to generate the proofs if she has cheated. Overall, we can make this non-interactive (NI), by allowing Peggy the chance to create her own challenges, and then present these with the proofs.
Coding
The outline coding using the library from the Krytology library is defined below. The first modulus is square free, and the second one is a square [here]:
package main
import (
"crypto/rand"
"fmt"
"math"
"math/big"
"os"
"strconv"
crypto "github.com/coinbase/kryptology/pkg/core"
)
func main() {
nobits:=5
argCount := len(os.Args[1:])
if argCount > 0 {
nobits,_ = strconv.Atoi(os.Args[1])
}
p, _ := rand.Prime(rand.Reader, nobits)
q:=p
for {
q, _ = rand.Prime(rand.Reader, nobits)
if p.Cmp(q) != 0 { break }
}
N := new(big.Int).Mul(p, q)
PHI := new(big.Int).Mul(new(big.Int).Sub(p, big.NewInt(1)), new(big.Int).Sub(q, big.NewInt(1)))
M, _ := crypto.Inv(N, PHI)
x, _ := rand.Int(rand.Reader, new(big.Int).SetUint64(uint64(math.Pow(2, float64(nobits)))))
proof, _ := crypto.Exp(x, M, N)
fmt.Printf("p=%s\n", p)
fmt.Printf("q=%s\n", q)
fmt.Printf("M=%s\n", M)
fmt.Printf("N=%s\n", N)
fmt.Printf("PHI=%s\n", PHI)
fmt.Printf("\nChallenge:\t%v\n", x)
fmt.Printf("Proof:\t%v\n", proof)
lhs, _ := crypto.Exp(proof, N, N)
fmt.Printf("Proof^N (mod N):\t%v\n", lhs)
proven := true
if lhs.Cmp(x) != 0 {
proven = false
}
if proven == true {
fmt.Printf("\nZero knowledge proof of safe Paillier\n")
} else {
fmt.Printf("\nNo Zero knowledge proof of safe Paillier\n")
}
fmt.Printf("\n\n== Now trying with an incorrect value of N=p^2 ==\n")
N = new(big.Int).Mul(p, p)
PHI = new(big.Int).Mul(new(big.Int).Sub(p, big.NewInt(1)), new(big.Int).Sub(p, big.NewInt(1)))
M, _ = crypto.Inv(N, PHI)
x, _ = rand.Int(rand.Reader, new(big.Int).SetUint64(uint64(math.Pow(2, float64(nobits)))))
proof, _ = crypto.Exp(x, M, N)
fmt.Printf("p=%s\n", p)
fmt.Printf("M=%s\n", M)
fmt.Printf("N=%s\n", N)
fmt.Printf("\nChallenge:\t%v\n", x)
fmt.Printf("Proof:\t%v\n", proof)
lhs, _ = crypto.Exp(proof, N, N)
fmt.Printf("Proof^N (mod N):\t%v\n", lhs)
proven = true
if lhs.Cmp(x) != 0 {
proven = false
}
if proven == true {
fmt.Printf("\nZero knowledge proof of safe Paillier\n")
} else {
fmt.Printf("\nNo Zero knowledge proof of safe Paillier\n")
}
}A sample run is [here]:
p=3163
q=3697
M=6045283
N=11693611
PHI=11686752
Challenge: 781
Proof: 8494942
Proof^N (mod N): 781
Zero knowledge proof of safe Paillier
== Now trying with an incorrect value of N=p^2 ==
p=3163
M=9991921
N=10004569
Challenge: 3072
Proof: 2998433
Proof^N (mod N): 5674331
No Zero knowledge proof of safe Paillierand [here]:
p=338866964140043411468873848695275241571
q=303416071899795017719693767589867444787
M=2667416890610086376756756543888369247051051012931162538919083196037004544533
N=102817683155980671680331235902830578322249490715746792929396448502149929640377
PHI=102817683155980671680331235902830578321607207679706954500207880885864786954020
Challenge: 5778954262180670354
Proof: 17541698715363339637339111063123573377678392333813998745320388206205518554463
Proof^N (mod N): 5778954262180670354
Zero knowledge proof of safe Paillier
== Now trying with an incorrect value of N=p^2 ==
p=338866964140043411468873848695275241571
M=114830819385489467364932280308566871929518427848663364068580836562831305581761
N=114830819385489467364932280308566871930873895705223537714456331957612406548041
Challenge: 3182905517568311201
Proof: 101673933567844850137914416419994421527326217936079135451976555636417860079774
Proof^N (mod N): 80939508196207850652294141501902064755098489726530492563801723952829877603051
No Zero knowledge proof of safe PaillierSo what?
We use a square-free Paillier method for the Gennaro and Goldfeder’s threshold ECDSA protocol (see Phase 3 of the key generation protocol):

The GG20 (Gennaro, R., & Goldfeder, S. (2020) [2]) method implements an ECDSA signing algorithm using threshold protocols. In this case, Bob and Alice will communicate using a DKG method, and then Bob will be able to create a valid signature. We can use the Kryptology library developed by Coinbase to implement 2-of-2 threshold ECDSA signing algorithm of the GG20 method. Once Bob and Alice have communicated, Bob will hold a signature for the message. We will then check this signature for its validity. We will thus split a private key up into two secret shares and then will be able to sign with the shares of the key:
https://asecuritysite.com/signatures/sss_gg02
References
[1] Goldberg, S., Reyzin, L., Sagga, O., & Baldimtsi, F. (2019, November). Efficient noninteractive certification of RSA moduli and beyond. In Advances in Cryptology–ASIACRYPT 2019: 25th International Conference on the Theory and Application of Cryptology and Information Security, Kobe, Japan, December 8–12, 2019, Proceedings, Part III (pp. 700–727). Cham: Springer International Publishing.
[2] Gennaro, R., & Goldfeder, S. (2020). One Round Threshold ECDSA with Identifiable Abort. IACR Cryptol. ePrint Arch., 2020, 540.