Proving I Have the Private Key for a Given Public Key Without Giving It Away

Proving I Have the Private Key for a Given Public Key Without Giving It Away
Proof of Factorization
We need to build systems that have proofs embedded into them. For this, we can use Zero Knowledge Proofs (ZKPs), and which allow us to prove something, without giving away our secrets. So, let’s take an example of a proof. In this case, we will use RSA encryption. With this, we start with two random prime numbers (p and q), and then create a modulus:

From here, we then compute:

and select the public exponent (e) which does not share a factor with PHI, and then compute private exponent (d):

The public key is then (e,N) and the private key is (d,N). With this only if we know p and q can we compute PHI correctly. For a proof that we know these, we can use this paper [1]:

In the paper, we have the simple proof of:
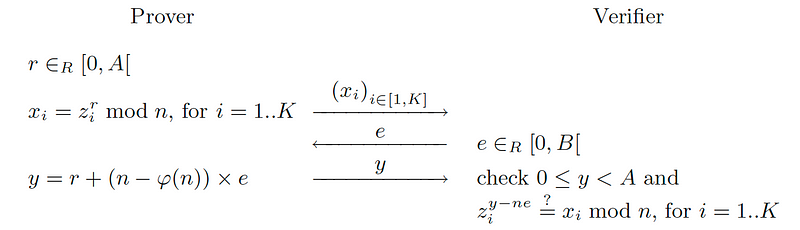
In the paper, Peggy selects a random value (x) and r and then computes:

Peggy then sends that to Victor. Victor then sends a random challenge valiue of e to Peggy. Peggy then computes the commitment of:

Peggy sends y to Victor, and who computes:

If P is equal to the value that Peggy send for x, Peggy has proven that she knowns p and q.
Now, let’s implement one proof for Victor (the Verifier) proving that Peggy (the Prover) does have the required knowledge of p and q. In this case, we will create a proof when we know p and q, and another when we do not:
Now, let’s implement one proof for Victor (the Verifier) proving that Peggy (the Prover) does have the required knowledge of p and q.
The outline coding using the library from the Krytology library. In this case, we will create a proof when we know p and q, and another when we do not [here]:
package main
import (
"crypto/rand"
"fmt"
"math"
"math/big"
"os"
"strconv"
crypto "github.com/coinbase/kryptology/pkg/core"
)
func main() {
nobits:=5
argCount := len(os.Args[1:])
if argCount > 0 {
nobits,_ = strconv.Atoi(os.Args[1])
}
p, _ := rand.Prime(rand.Reader, nobits)
q:=p
for {
q, _ = rand.Prime(rand.Reader, nobits)
if p.Cmp(q) != 0 { break }
}
N := new(big.Int).Mul(p, q)
PHI := new(big.Int).Mul(new(big.Int).Sub(p, big.NewInt(1)), new(big.Int).Sub(q, big.NewInt(1)))
z, _ := rand.Int(rand.Reader, new(big.Int).SetUint64(uint64(math.Pow(2, float64(nobits)))))
r, _ := rand.Int(rand.Reader, new(big.Int).SetUint64(uint64(math.Pow(2, float64(nobits)))))
e, _ := rand.Int(rand.Reader, new(big.Int).SetUint64(uint64(math.Pow(2, float64(nobits)))))
x, _ := crypto.Exp(z, r, N)
y:= new(big.Int).Add(r,new(big.Int).Mul(e,new(big.Int).Sub(N, PHI) ))
check:= new(big.Int).Exp(z,new(big.Int).Sub(y,new(big.Int).Mul(N,e)),N)
fmt.Printf("p=%s\n", p)
fmt.Printf("q=%s\n", q)
fmt.Printf("PHI=%s\n", PHI)
fmt.Printf("Peggy sends\tx=%s\n", x)
fmt.Printf("\nVictor send\te:\t%v\n", e)
fmt.Printf("Peggy creates proof:\t%s\n", y)
fmt.Printf("Alices computes:\t%s\n", check)
if (check.Cmp(x)==0) {
fmt.Printf("Proof of factoring has been proven (Check==x)\n\n")
} else {
fmt.Printf("Proof of factoring has not been proven (Check!=x)!\n\n")
}
// Now we can prove that we don't know p and q
PHI,_ = rand.Prime(rand.Reader, 2*nobits-1)
z, _ = rand.Int(rand.Reader, new(big.Int).SetUint64(uint64(math.Pow(2, float64(nobits)))))
r, _ = rand.Int(rand.Reader, new(big.Int).SetUint64(uint64(math.Pow(2, float64(nobits)))))
e, _ = rand.Int(rand.Reader, new(big.Int).SetUint64(uint64(math.Pow(2, float64(nobits)))))
x, _ = crypto.Exp(z, r, N)
y= new(big.Int).Add(r,new(big.Int).Mul(e,new(big.Int).Sub(N, PHI) ))
check= new(big.Int).Exp(z,new(big.Int).Sub(y,new(big.Int).Mul(N,e)),N)
fmt.Printf("p=%s\n", p)
fmt.Printf("q=%s\n", q)
fmt.Printf("PHI=%s\n", PHI)
fmt.Printf("Peggy sends\tx=%s\n", x)
fmt.Printf("\nVictor send\te:\t%v\n", e)
fmt.Printf("Peggy creates proof:\t%s\n", y)
fmt.Printf("Alices computes:\t%s\n", check)
if (check.Cmp(x)==0) {
fmt.Printf("Proof of factoring has been proven (Check==x)\n\n")
} else {
fmt.Printf("Proof of factoring has not been proven (Check!=x)!\n\n")
}
}A sample run for small values of p and q is [here]:
== Proving that we know p and q from N ==
p=977147
q=844183
PHI=824889064572
Peggy sends x=551677896191
Victor send e=699488
Peggy creates proof: y=1273997833776
Victor computes: check=551677896191
Proof of factoring has been proven (Check==x)
p=977147
q=844183
PHI=417237265201 (Wrong!)
Peggy sends x=107924963359
Victor send e=192228
Peggy creates proof: y=78362440200289867
Victor computes: check=75431611685
Proof of factoring has not been proven (Check!=x)!and for larger values of p and q [here]:
== Proving that we know p and q from N ==
p=275585967753873600716436326628783455093
q=325811021881245009809152134474416310439
PHI=89788945770021393410895476147876251415588122774903509882566263945204503850296
Peggy sends x=46161062772438767255050447624329295660196379472974413133815467402139274903277
Victor send e=5133636032052576888
Peggy creates proof: y=3087353255558795013755518173975136272483773268701241280194
Victor computes: check=46161062772438767255050447624329295660196379472974413133815467402139274903277
Proof of factoring has been proven (Check==x)
p=275585967753873600716436326628783455093
q=325811021881245009809152134474416310439
PHI=55836793355946276284079447102831505977497406442842698992400374835180476535857
Peggy sends x=71131768330117980540927663247594149553192242760047028226045269498340554091291
Victor send e=2993994638442759910
Peggy creates proof: y=101652562291332308354071338565624751920060542454454212603520191933344685040403733304452187915998
Victor computes: check=40971809361411454192610163799959001012838226461914173998837761298339999877650
Proof of factoring has not been proven (Check!=x)!And, so, what we have basically done here, is to prove that Peggy can actually factorize a modulus (N). And, while I have presented an Interactive ZKP, we can easily convert to a Non-interactive ZKP (NI-ZKP), and where Peggy can create her own challenge.
Conclusions
We need to move into a world where we can prove knowledge rather than give it away. So, welcome to the world of ZKPs:
https://asecuritysite.com/zero
References
[1] Poupard, G., & Stern, J. (2000, January). Short proofs of knowledge for factoring. In Public Key Cryptography (Vol. 1751, pp. 147–166) [here].