kth root of n (mod p)

kth root of n (mod p)

What is the 7th root of 2 (mod 13)? Well, the answer is 11, and I will show you how we get this. In this article we will solve the kth root of n (modulo p) and find the result:

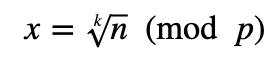
For this we need to find the value of k so that: n^k (mod p)=x, and using the using the Extended Euclidean method. Note, it will only work when gcd(k,p−1) is equal to 1.

Normal roots

In maths, we should know that:

and that:

But, in discrete methods, we need solve the kth root of n modulo p and find the result:

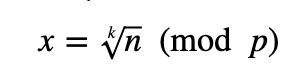
For this we need to find the value of x so that:

One of the most prominate methods is the Euclidean method, and which determines the largest common factor (gcd — greatest common denominator) between two numbers. For example:

gcd(27,9) = 3
gcd(27,13) =1

In cryptography, we often focus on making sure that two values do not share the same factor, and thus often use gcd(a,b)=1. Another widely used method is known as the Extended Euclidean method, and where we find a solution for:

a.x+b.y=gcd(a,b)

and where we know a and b and want to discover x and y. In this case gcd(a,b) defines the greatest common factor between a and b. If a and b do not share a factor, the gcd() will be 1. For example, if a=5 and b=6, we can use the Extended Euclidean method (xgcd()) with:

import libnum
a=5
b=6
(x,y,r) = libnum.xgcd(a,b)
print (x,y,r)

This gives:

-1 1 1

In this case we have −1(5)+1(6)=1 and which is true. If we now try b=8, we get a result of:

-3 2 1

This gives us −3(5)+2(8)=1 and which is true.

RSA and Extended Euclidian

One of the best usages of the Extended Euclidian method is in RSA encryption. For this, we take two prime numbers (p and q) and determine the public modulus (N):

N=p.q

Next we compute φ:

φ=(p−1).(q−1)

We then pick our encryption exponent (e) to not share a factor with φ, then compute the decryption exponent (d) with:

d.e=1(modφ)

and which is equivalent to:

d⋅e+φ.t=1

This is in the form of the Extended Euclidian method and which gives a solution of d and t. We can compute the value of d with:

(d,_,r) = libnum.xgcd(e,PHI)

The code to implement this is:

>>> e=7
>>> p=97
>>> q=101
>>> N=p*q
>>> PHI=(p-1)*(q-1)
>>> import libnum
>>> print (libnum.gcd(e,PHI))
1
>>> (d,_,r) = libnum.xgcd(e,PHI)
>>> print (d,r)
2743 1
>>> print (d*e % PHI)
1

We can now encrypt and decrypt with these values:

>>> M=5
>>> C=pow(M,e,N)
>>> print (C)
9546
>>> Rec=pow(C,d,N)
>>> print (Rec)
5

Determine k-th root of n(mod p)

We can use the Extended Euclidian method to determine the k-th root of a value (n) modulo p. With this, for k√n (mod p), and if gcd(k,p−1)=1, there exists a solution of m and t for:

m.k+t.(p−1)=1

This is in the form of the Extended Euclidian method, and the solution is then [1]:

nm=k√n (mod p)

The code to find the value of m and the root is then:

import sys
from libnum import xgcd
def findnroot(n,k,p):
    (m,s,v) = xgcd(k,p-1)
    if (v==1):
        return(pow(n,m,p))

A few examples of these are [here]:

2nd root of 5 (mod 11) = None
3rd root of 5 (mod 11) = 3
4th root of 5 (mod 11) = None
5th root of 5 (mod 11) = None
6th root of 5 (mod 11) = None
7th root of 5 (mod 11) = 4
8th root of 5 (mod 11) = None
9th root of 5 (mod 11) = 9
10th root of 5 (mod 11) = None

Thus:

[3rd root of 5 (mod 11) = 3] -> 3³ (mod 11) gives you 5

[7th root of 5 (mod 11) = 4] -> 4⁷ (mod 11) you get 5.

Notice, there are a few that do not give any roots, as there is no basic solution for that root. This is either because there is no root, or that the gcd(k,n-1) is not equal to 1.

Some simple code which uses the Extended Euclidian method for the root is [here]:

import sys
from libnum import xgcd
def findnroot(n,k,p):
    (m,s,v) = xgcd(k,p-1)
    if (v==1):
        return(pow(n,m,p))
        
p=17
n=2
if (len(sys.argv)>1):
    n=int(sys.argv[1])
if (len(sys.argv)>2):
    p=int(sys.argv[2])
    
for root in range(2,p):
    if (root>50): break
    v=findnroot(n,root,p)
    if (root==2): print(f"{root}nd root of {n} (mod {p}) = {v}")
    elif (root==3): print(f"{root}rd root of {n} (mod {p}) = {v}")
    else: print(f"{root}th root of {n} (mod {p}) = {v}")

Conclusions

So what is the 7th root of 2 (mod 13)?

The answer is 11, as:

11⁷ (mod 13) = 19,487,171 (mod 13) = 2