Proof of Shuffle Using Homomorphic Encryption (and ElGamal Encryption)

We all know how to shuffle (or mix) cards. But, a skilled dealer can trick us into thinking that cards have been shuffled, but where they…

Proof of Shuffle Using Homomorphic Encryption (and ElGamal Encryption)

We all know how to shuffle (or mix) cards. But, a skilled dealer can trick us into thinking that cards have been shuffled, but where they manage to put certain cards in the right place. If done for gain, it is cheating, and if done for fun, it is probably a magical trick. Within an encryption system we can perform a blind shuffle where we can encrypt our data so that the dealer cannot see the cards that are being shuffled, and then for there to be a mixing process. In a trusted system, we have several nodes who each perform the same shuffle operation, and where we know that — if at least one node is honest, the shuffle will be honest. This is known as a mix-net.

In 2001, Neff [1] proposed a shuffling method that provides a proof of shuffle, and where each mix node does not require the public key of the cipher text. This is achieved using homomorphic encryption, such as using ElGamal or lattice methods:

In a re-encryption mix net, the input to the mixer is encrypted ciphertext. We then have a mixing phase where all the ciphertexts are shuffled and then re-encrypted. Next, we decrypt all the ciphertext. The mixer is normally done by one server, and the decryption by another.

Key generation: First we generate a private key (x), and an ElGamal public key (Y,g,q). The private key is shared across all the decryption servers as a secret share (with a t from n threshold). The basic steps are:

Input values: The input message (M) is encrypted (g^r,M.Y^r), and where r is a random number, and M is the plain text message.
Mixing phase: Each mixer server then permutes and re-encrypts each ciphertext.
Decryption: Jointly the decryption servers join together to perform threshold decryption of the output.

So, how can we keep encrypting with each mixer node, but still decrypt at the end? With ElGamal encryption, initially, Bob creates a public key by selecting a g value and a prime number (p) and then selecting a private key (x). He then computes Y which is:

Y=g^x (mod p)

The public key is (Y,g,p) and he will send this to Alice. Initially, she has a message (M) and selects a random value k. She then computes a and b:

a=g^k (mod p)

b=Y^k.M (mod p)

To decrypt this we use:

Now, let’s encrypt with the mixer node. To encrypt a first time, the first node generates a random value (k_1) to give:

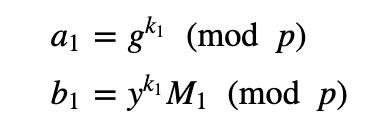
Now, a second node can also encrypt with:

Then we get:

and then:

and so we can keep encrypting but were a single end decryption process can then decrypt the answer. And, so, each of the mixer nodes can perform a shuffle, and then re-encrypt each of the ciphertexts it receives.

Coding

We can use the ElGamal homomorphic method to create a proof of shuffle from each node [here]. In this case, we will create five key pairs, and then encrypt each of the private keys with the public key of the server. Next, we will shuffle the encrypted private keys and produce the proof. The server key pair is (h,H), the key pairs are (c_k,C_k), and the encrypted keys for each client (k) is (X_k,Y_k). These are then shuffled to give (Xbar_k,Ybar_y) [here]:



// Based on https://github.com/dedis/kyber/blob/master/shuffle/shuffle_test.go
package main

import (


 "go.dedis.ch/kyber/v3"
 proof "go.dedis.ch/kyber/v3/proof"
 "go.dedis.ch/kyber/v3/shuffle"
 "fmt"
 "go.dedis.ch/kyber/v3/group/edwards25519"

 
)

func main() {
k := 5 // Number of mixers

suite := edwards25519.NewBlakeSHA256Ed25519()


rand := suite.RandomStream()

 // Create a "server" private/public keypair
 h := suite.Scalar().Pick(rand)
 H := suite.Point().Mul(h, nil)

 // Create a set of ephemeral "client" keypairs to shuffle
 c := make([]kyber.Scalar, k)
 C := make([]kyber.Point, k)
 // fmt.Println("\nclient keys:")
 for i := 0; i < k; i++ {
  c[i] = suite.Scalar().Pick(rand)
  C[i] = suite.Point().Mul(c[i], nil)
  
 }

 // ElGamal-encrypt all these keypairs with the "server" key
 X := make([]kyber.Point, k)
 Y := make([]kyber.Point, k)
 r := suite.Scalar() // temporary
 for i := 0; i < k; i++ {
  r.Pick(rand)
  X[i] = suite.Point().Mul(r, nil)
  Y[i] = suite.Point().Mul(r, H) // ElGamal blinding factor
  Y[i].Add(Y[i], C[i])           // Encrypted client public key
 }


 Xbar, Ybar, prover := shuffle.Shuffle(suite, nil, H, X, Y, rand)
 prf, err := proof.HashProve(suite, "PairShuffle", prover)
 if err != nil {
  panic("Shuffle proof failed: " + err.Error())
 }

 fmt.Printf("Before shuffle (X):\n%v\n",X)
 fmt.Printf("After shuffle (X):\n%v\n",Xbar)
 fmt.Printf("Before shuffle (Y):\n%v\n",X)
 fmt.Printf("After shuffle (Y):\n%v\n",Xbar)

 fmt.Printf("\nProof (first 16 bytes):\n%x\n",prf[:32])

 verifier := shuffle.Verifier(suite, nil, H, X, Y, Xbar, Ybar)
 err = proof.HashVerify(suite, "PairShuffle", verifier, prf)
 if err == nil {
   fmt.Printf("Shuffle proven")
 }



}

A sample run gives [here]:

Before shuffle (X):
[1dc732dde8967da661762c65db960097766536247d10273cfbca5676668eccfb 7c15fc5d341b3edcb56a3389f8e3af6990757a5b3d3f98d7f0a7a44c79d8c1e7 63a13a1aee7f3246e19c8f36bf605941c86ebd13e4059a4250c76c919cda10c9 d5936a5d33f5a53f55efd51220d5172146b76b69401949d1278a5e046e209ae0 25fe94cfa7f65ce4a85210fbe86ecb4c126a1eda9fbf6a612d7919bdf440d736]
After shuffle (X):
[ee0aa2b85433b67684cce1b8a93c504dcd1cdb018fa473714c5a9b869439799f 0037b4dbe1e64cd20d9a1dfd4f75557e97f634d3c0ecd2bfd194fb58a54b6a3b 8b5028c4e354f724dd401ec2bc5d3ce16b4a3d584d4880ea9222cd5f89d61e15 9cb9b47aeeaf409f788267f60add91e3449d4565816cf10f84d90ba430b4e9ac 2e5a5dcebf7b1842643359edddebde1391c6f9f3533a3aa185380f977b4146a1]
Before shuffle (Y):
[1dc732dde8967da661762c65db960097766536247d10273cfbca5676668eccfb 7c15fc5d341b3edcb56a3389f8e3af6990757a5b3d3f98d7f0a7a44c79d8c1e7 63a13a1aee7f3246e19c8f36bf605941c86ebd13e4059a4250c76c919cda10c9 d5936a5d33f5a53f55efd51220d5172146b76b69401949d1278a5e046e209ae0 25fe94cfa7f65ce4a85210fbe86ecb4c126a1eda9fbf6a612d7919bdf440d736]
After shuffle (Y):
[ee0aa2b85433b67684cce1b8a93c504dcd1cdb018fa473714c5a9b869439799f 0037b4dbe1e64cd20d9a1dfd4f75557e97f634d3c0ecd2bfd194fb58a54b6a3b 8b5028c4e354f724dd401ec2bc5d3ce16b4a3d584d4880ea9222cd5f89d61e15 9cb9b47aeeaf409f788267f60add91e3449d4565816cf10f84d90ba430b4e9ac 2e5a5dcebf7b1842643359edddebde1391c6f9f3533a3aa185380f977b4146a1]

Proof (first 16 bytes):
de5dc75093c4f105fceb7bc45d31660fe92e5a3ba47fe58b57ce0ca9b2e0a3b7
Shuffle proven

And, there you go, and verifiable (and secret) shuffle using homomorphic encryption:

https://asecuritysite.com/zero/go_shuffle

We can also use lattice-based methods to replace the ElGamal technique, as lattice-based methods enable full homomorphic encryption (while ElGamal only gives partial homomorphic encryption) [2]:

References

[1] Neff, C. A. (2001, November). A verifiable secret shuffle and its application to e-voting. In Proceedings of the 8th ACM conference on Computer and Communications Security (pp. 116–125).

[2] Costa, N., Martínez, R., & Morillo, P. (2020). Lattice-based proof of a shuffle. In Financial Cryptography and Data Security: FC 2019 International Workshops, VOTING and WTSC, St. Kitts, St. Kitts and Nevis, February 18–22, 2019, Revised Selected Papers 23 (pp. 330–346). Springer International Publishing.