ElGamal Encryption with Elliptic Curves

ElGamal Encryption with Elliptic Curves

Towards partial homomorphic encryption with elliptic curves

I think if John Napier were alive today he would wonder at how discrete logarithms have been used to secure our world. And, I am also sure he would strike up an immediate bond with Taher Elgamal and who, in 1985, published this classic paper [here]:

Within the paper, he proposed the ElGamal discrete logarithm encryption system and also the ElGamal signature scheme (and which became the core of the DSA signature method). In 2009, Elgamal was awarded the RSA Conference 2009 Lifetime Achievement Award, and where he was dubbed the “father of SSL”.

At the core of the ElGamal public key methods is the Discrete Logarithm Problem, and where we have:

Y= g^x (mod p)

and where it is difficult to determine x, even if we have Y, g and p (as long as p is a large enough prime number). And so it is used in the Diffie-Hellman method for key exchange. We also use it to sign a message, and where we create a key pair (a public key and a private key). The private key is used to encrypt something (such as the hash of the message), and then the public key is used to prove the signing.

With ElGamal, initially, Alice creates her public key by selecting a g value and a prime number (p) and then selecting a private key (x). She then computes Y which is [here]:

Her public key is (Y,g,p) and she will send this to Bob. Bob then creates a message (M) and selects a random value (r). She then computes a and b:

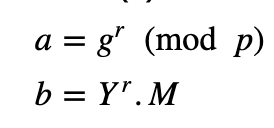
Bob then receives these and decrypts with:

Thus works as:

You can try this here.

ElGamal and ECC

But, Elliptic Curve Cryptography (ECC) methods are just everywhere just now. With ECC, we take points on a defined curve — such as Curve 25519 — and then perform point addition and subtraction. So how can we convert the ElGamal method into ECC? First, Alice first creates a private key (x) — and which is a random scalar value — and a public key (x.G) — and which is a point on the elliptic curve. P is the base point on a curve. Alice’s public key will then be:

Y=x.G

If Bob wants to send Alice an encrypted message (M), he creates a random value (r) and uses her public key (Y) to produce a cipher message of:

C1=r.G

and then the next with:

C2=r.Y+M

and where M is matched to a point on the elliptic curve. Now Alice receives (C1 and C2), and computes:

M=C1-x.C2

As C and S will be points on the elliptic curve, this will be done with a point subtraction operation. Overall this will recover the original message as:

M=C2−y.C1=r.x.G+M−x.r.G=M

The following is some Go code to implement this [here]:

package main

import (
 crand "crypto/rand"
 "fmt"
 "math"
 "math/big"
 "math/rand"
 "os"
 "time"

 "github.com/coinbase/kryptology/pkg/core/curves"
)

func powInt(x, y int) int {
 return int(math.Pow(float64(x), float64(y)))
}

func encrypt(c *curves.Curve, msg [] byte,G curves.Point, Y curves.Point) (C1 curves.Point, C2 *big.Int) {

 x :=new(big.Int).SetBytes(msg)
 r := c.Scalar.Random(crand.Reader)

 rY := Y.Mul(r)
 rG := G.Mul(r)
 rYval := new(big.Int).SetBytes(rY.ToAffineUncompressed())
 C2 = new(big.Int).Add(rYval, x)
 C1 = rG
 return
}
func decrypt(x curves.Scalar, C1 curves.Point, C2 *big.Int) (p []byte) {
 xC := C1.Mul(x)
 xCval := new(big.Int).SetBytes(xC.ToAffineUncompressed())
 p = new(big.Int).Sub(C2, xCval).Bytes()
 return
}

func main() {

 argCount := len(os.Args[1:])

 msg := "Hello"

 if argCount > 0 {
  msg = os.Args[1]
 }


 rand.Seed(time.Now().UnixNano())

 curve := curves.K256()
 G := curve.Point.Generator()


 x := curve.Scalar.Random(crand.Reader)

 Y := G.Mul(x)

 C1, C2 := encrypt(curve, [] byte(msg), G, Y)

 x_decrypted := decrypt(x, C1, C2)

 fmt.Printf("Message: %s\n", msg)
 fmt.Printf("\nx=%x\nY=%x\n", x.Bytes(),Y.ToAffineUncompressed())
 fmt.Printf("\nC1=%x\nC2=%s\n", C1.ToAffineUncompressed(), C2)
 fmt.Printf("\nDecrypted: %s\n", string(x_decrypted))

}

A sample run is [here]:

Message: Hello

x=85690c51b228b614b515604f0d999cd1a28df605bac97d34633a0e7b86ee3c85
Y=04a03a7988620d1dafdb2baae48d5638ede01f7c00d7ca8430baf0ef17353920f341e55647c3fcde1fc6bf479724fd42276ddca4aa9ecf3c924d2048d2ed721157

C1=040775436fb3ec20816a85c50253b7bf3b82ac5bcc1e372b4f7bd7d812b9a675f0ac8d739fe5122dfba4cb798f9273e2e1483b22cd6347d36cb9b96df720f8a2fd
C2=57874734037032100445317653665255429180084300986380534544295609387996620841581470710462217777364540827711653593330226141760413561202423334955662883749773613

Decrypted: Hello

Conclusions

And there you go, ElGamal using ECC:

https://asecuritysite.com/elgamal/elgamal02_str

In this article we have used the secp256k1 curve (as used in Bitcoin and Ethereum). If we want to use other curves, such as P256 and Curve 25519, we can implement with:

https://asecuritysite.com/elgamal/elgamal02_str2

Finally, the great advantage of using the ElGamal methods in elliptic curves is that it allows us to implement partial homomorphic encryption.