Homomorphic Multiplication and Division with RSA

Homomorphic Multiplication and Division with RSA

Ssh! RSA implements partial homomorphic encryption. With homomorphic encryption, we generate a key pair (a public key and a private key). We can encrypt data with the public key, and then operate on it in a homomorphic way, such as add, subtract, multiply and divide. The result of this can then be decrypted with the private key.

Homomorphic multiplication

So with RSA we cipher with:

is the encryption key, and N is the multiplication of two prime numbers (p and q). The difficuly in this is factorizing N to get two prime numbers. To decrypt, we find the decryption key (d) and then perform:

So if we take two values (a and b), then we can cipher them as:

If we multiply the ciphers we get:

This is then:

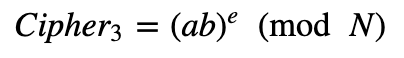
When we can then decrypt and determine the value of a times b.

Here is the code to implement this for randomly generated prime numbers [here]:

import sys
import libnum
from Crypto.Util.number import long_to_bytes,bytes_to_long
from Crypto import Random
import Crypto

bits=128

val1=99
val2=3

if (len(sys.argv)>1):
	val1=int(sys.argv[1])
if (len(sys.argv)>2):
	val2=int(sys.argv[2])
if (len(sys.argv)>3):
	bits=int(sys.argv[3])

p = Crypto.Util.number.getPrime(bits, randfunc=Crypto.Random.get_random_bytes)
q = Crypto.Util.number.getPrime(bits, randfunc=Crypto.Random.get_random_bytes)

N=p*q
PHI=(p-1)*(q-1)
e=65537
d=libnum.invmod(e,PHI)


cipher1 = pow(val1,e,N)
cipher2 = pow(val2,e,N)

result = (cipher1 * cipher2) % N


decipher = pow(result,d,N)


print ("========")
print ("e is=",e)

print ("d is=",d)
print ("n is=",N)
print ("========")
print ("val1 is=",val1)
print ("val2 is=",val2)
print ("========")

print ("Cipher1 is=",cipher1)

print ("Cipher2 is=",cipher2)
print ("Cipher fusion is=",result)
print ("========")
print ("Result is=",decipher)

And a sample run is [here]:

========
e is= 65537
d is= 553423196544212726857099726883531153
n is= 1084490372919449514104313110499093857
========
val1 is= 11
val2 is= 5
========
Cipher1 is= 954113378987226340611682671019806370
Cipher2 is= 136633440216385349708415165586147485
Cipher fusion is= 916813400938594915084504889870421321
========
Result is= 55

Homomorphic division

RSA is a partially homomorphic crypto system. By the wonder of John Napier we get:

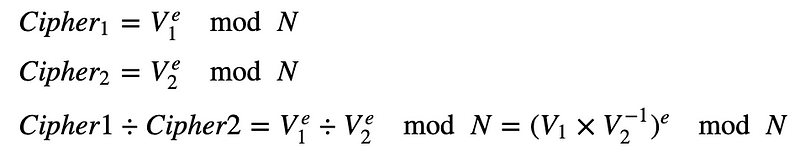
To perform V2^{−1) we perform the inverse of V2 (mod N).

An outline of the code is here:

import sys
import libnum
from Crypto.Util.number import long_to_bytes,bytes_to_long
from Crypto import Random
import Crypto
bits=128
val1=99
val2=3
if (len(sys.argv)>1):
 val1=int(sys.argv[1])
if (len(sys.argv)>2):
 val2=int(sys.argv[2])
if (len(sys.argv)>3):
 bits=int(sys.argv[3])
p = Crypto.Util.number.getPrime(bits, randfunc=Crypto.Random.get_random_bytes)
q = Crypto.Util.number.getPrime(bits, randfunc=Crypto.Random.get_random_bytes)
N=p*q
PHI=(p-1)*(q-1)
e=65537
d=libnum.invmod(e,PHI)

cipher1 = pow(val1,e,N)
cipher2 = pow(val2,e,N)
result = (cipher1 * libnum.invmod(cipher2,N)) % N
decipher = pow(result,d,N)

print ("========")
print ("e is=",e)
print ("d is=",d)
print ("n is=",N)
print ("========")
print ("val1 is=",val1)
print ("val2 is=",val2)
print ("========")
print ("Cipher1 is=",cipher1)
print ("Cipher2 is=",cipher2)
print ("Cipher fusion is=",result)
print ("========")
print ("Result is=",decipher)

A sample run is [here]:

========
e is= 65537
d is= 28950357214703222362017139956495142657348786818956975799148785377956873620401
n is= 41166429316756820151001698915767800654248393492359393724253968689821998507811
========
val1 is= 99
val2 is= 3
========
Cipher1 is= 14732275788451800549705537518890490107891520021485483541129431374974346830182
Cipher2 is= 11780774532139055846856872916828708532948466679005746087280018752766099115556
Cipher fusion is= 17791762151312970555472705442447740832156079928115533374059406733722456936614
========
Result is= 33

Conclusions

And there you go. If you need multiplication or division with homomorphic encryption, then RSA is a contender.