How Many Things Can You Count To on Your Fingers?

Let’s talk about zero — that pesky number!

How Many Things Can You Count Up To On Your Fingers?

Let’s talk about zero — that pesky number!

For the count on your fingers? Well, let’s try ..

0 … 1 … 2 … 3 … 4 … 5 … 6 … 7 … 8 … 9 … 10

That’s 11! That pesky zero has managed to muscle itself into our counting. Zero, itself, is a valid number of our count, as we need to tell someone that we have no items.

But zero causes many problems in programming, as we need to know where we start our indexing. Should we start at zero and count up, or should we start at 1? And, if we want n elements, do we count up to n, or n-1? This is especially important when we are indexing our array elements, as we compute the location in memory and which relates to its index value and the number of bytes that each element represents.

In Pascal, to count from 1 to 10:

n: array [1..10] of integer;
   for i:= 1 to 10 do
      writeln('[', i, '] = ', n[i] );

But, in C, we would use:

  int n[5];

  for(int i = 0; i < 5; ++i) {
     printf("%d", n[i]);
  }

In the C example, our last element is n[4] and which is the fifth element. A standard novice issue is to access the n[5] element (and which is unallocated):

int n[5];

  for(int i = 0; i <= 5; ++i) {
     printf("%d", n[i]);
  }

In this case, the compiler is likely to allow this, and will actually display the the contents of the memory after the area allocated for the array (and which could contain sensitive information). This is typically known as a buffer overflow.

Dividing by zero

As we should all know from our school days when you divide by zero, your calculator will just give up, and will typically display “NaN” — Not A Number. Luckily, most programming languages, too, catch this problem with an exception. But, if not caught, a program is likely to crash (or at least end with an exception). But, “Not A Number” is perhaps not quite correct, as the number just happens to be infinity — it’s just that our programming languages catch the zero value quickly, and return“NaN”. But, mathematically, we are incorrect in seeing the result as infinity.

Let’s count down for the value of b, and compute:

a=100
for b in range(10,-1,-1):
 print(a/b)

We get:

10.0
11.11111111111111
12.5
14.285714285714286
16.666666666666668
20.0
25.0
33.333333333333336
50.0
100.0
ZeroDivisionError: division by zero

For this, we are increasing in value as we get nearer zero for the divide. The limit of a divide by zero, is thus positive infinity. But, now if we count up from a negative number to zero:

a=100
for b in range(-10,1,1):
 print(a/b)

This gives us:

-10.0
-11.11111111111111
-12.5
-14.285714285714286
-16.666666666666668
-20.0
-25.0
-33.333333333333336
-50.0
-100.0
ZeroDivisionError: division by zero

Now, we see that we are increasing as a negative value, and will approach a limit of negative infinity. The way for a computer to test this is to make the divisor either a tiny negative value or a tiny positive value:

>>> a=10
>>> b=1e-100
>>> print (a/b)
1e+101
>>> b=-1e-100
>>> print (a/b)
-1e+101

But, what about zero divided by zero? What is that?

Let’s try it:

>>> a=0
>>> b=0
>>> print (a/b)
ZeroDivisionError: division by zero

But, for an equation of:

(a²-1)/(a-1)

what will the result be when a is unity, as we now have zero divided by zero? If we run, we get:

>>> a=1
>>> print ((a**2-1)/(a-1))
ZeroDivisionError: division by zero

With this, the Python program has caught the zero for the divisor, and just returned a division by zero exception. But this is wrong, as the answer is 2. Let’s experiment. Let’s make a just a little bit bigger than 1:

>>> a=1.0000001
>>> print ((a**2-1)/(a-1))
2.000000099920072

and again:

>>> a=1.0000000001
>>> print ((a**2-1)/(a-1))
2.0

and:

>>> a=1.0000000000001
>>> print ((a**2-1)/(a-1))
2.0

until we get:

>>> a=1.0000000000000001
>>> print ((a**2-1)/(a-1))
ZeroDivisionError: float division by zero

Thus, the computer has just given up, and easy it is to overflow its computations. If you are interested, the way we compute the limit as x approaches zero for:

In the case of (x²-1)/(x-1), we have the limit as x approaches 1. For this, we can expand to ((x+1)(x-1))/(x-1), and which gives x+1, and which gives +2.

Zero in cryptography

Why is zero such a problem? Well, to perform our cryptographic processing, we use mathematical operations, such as multiplication and division. As you should remember when we multiply by zero, we get zero, and when we divide by it, we get infinity. These operations will reset the calculation, and no matter what we do we can never recover any previous information from our value. We might also use exponents, and where g⁰ gives us unity.

Within our secure computations, we typically need to reverse an operation back to an original value. This often involves encrypting — performing a certain mathematical operation — and then decrypting — reversing the same mathematical operation.

For example, if we multiply a value of seven by four, and add three, we can compute:

Val = 7 * 4 + 3 = 31

and, to reverse, we just subtract 3 and divide by 4:

Res = (31 -3) /4 = 7

But, if I multiply by zero and then add three:

Val = 7 * 0+ 3 = 3

And reverse:

Val = (3–3)/0 = Infinity (or, who knows, as it is 0/0!)

And, so, we often want to avoid a value of zero, as it can short-circuit all our calculations and cause serious errors. Zero becomes are reset value, and where all previously computed values are lost. Thus, our computations should always check that we do not have a zero value, otherwise, all the answers we get are likely to be wrong. Even worse, we may continue to do our calculations, and get affirmative answers, such as incorrectly signing for data. In signatures, we often compare two values, but where a zero value for a public key could cause an invalid signature to be value.

Stopping zero values in discrete logs

In a finite field, we often use a (mod p) operation, and where p is a prime number. And so if we get a value which is a multiple of p we will also get a zero value. If p is 7, and if we have a message of 14, we will get:

Val = 14 (mod 7) = 0

This will equal zero, and where we will not be able to recover our value. For this, in discrete logs we have:

Val = g^x (mod p)

and where we pick g (the generator) so that we will never have a zero value. So it we have p=7, and can try different generator values [here]:

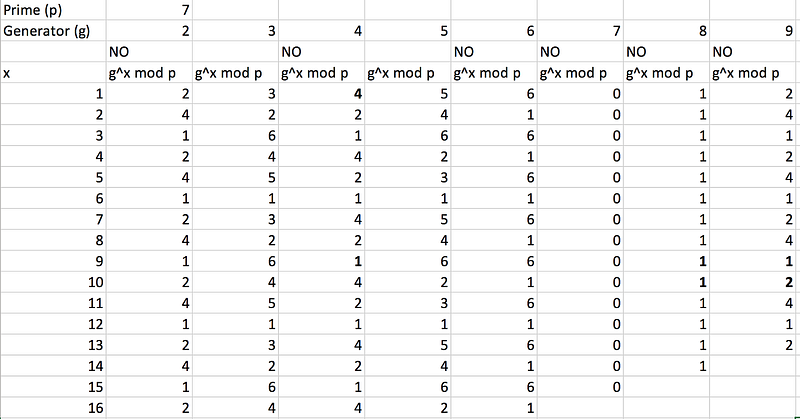
We can see that a value of g=2 does not work with p=7, as we do not output the full range of values (1 to 6), but g=3 works, as:

3¹ (mod 7) = 1
3² (mod 7) = 2
3³ (mod 7) = 6

and so on. We will then be able to map all these values back to the original values, and thus reverse the values. And, so, developers should check at important points that they are not getting zero values and that the base generator is correctly selected.

And, Eve, of course, doesn’t play by the rules and could trick Bob into short-circuiting his cryptography process.

Zero’s in elliptic curves

We have typically moved from discrete log methods into elliptic curve techniques, and where we deal with scalar values and elliptic curve points. If I have a private key of a, then my public key can be a.G, and where G is the base point on the curve. This is basically G+G+G … +G, and where the point G is added for a times. Overall, it is extremely difficult to determine a, if we have a.G and G.

But, elliptic curves have a zero problem, too. What happens if take a point p1, and then -p1, the addition of the points will be:

p = p1 — p1 = 𝑂

This is the zero point and is also defined as the point at infinity. In most elliptic curves, we basically just negate the y-coordinate value and keep the x co-ordinate value, the same. Eve could then trick Bob into using a weak generator value, that she can easily hack.

So now let’s look at a serious example of creating a zero point, and which can compromise an electronic wallet.

The Rogue Public Key

With BN256, we create the private key from a random number. This is a scalar value (sk1) and a public key mapped to the G2 curve:

pub_1=sk_1.G2

Next, we create a hash of the message (H(M)) and then create the signature of:

σ_1=sk1.H(M)

Next, we check the pair:

e(σ1,G_2)==e(H(m),pk_1)

This works because:

e(σ_1,G_2)==e(H(m),pk_1)

is:

e(x.H(M),G2)==e(H(m),pk1)

and:

e(H(M),x.G2)==e(H(m),pk1)

which is:

e(H(M),pk1)==e(H(m),pk1)

If lhs is equal to rhs, the pairing works, and the signature is verified.

Now we can aggregate the signatures. For the second set of keys, we now have a public key of:

pub2=sk2.G2

and where the second signature will be:

σ2=sk2.H(M)

Then the aggregated public key will be:

pk_a=pub1+pub2

Then the aggregated signature will be:

σ_a=σ1+σ2

The check is then:

e(σa,G2)==e(H(m),pk_a)

In the Rogue Public Key Attack, Eve can pretend that she is signing the message by creating a public key of:

pub2=−pub1

and a signature of:

σ2=−σ1

A negative value is fairly easy to implement, as we just need to make the y-axis value negative, and can leave the x-axis value the same. If Bob and Eve are signing a message (M), Bob will pass pk1 and σ1, and Eve will create a negative value of these, and pass pk2=−pk1 and σ2=−σ1. When the public keys and signatures are aggregated, we will get a zero value. Thus:

pk_a=0

σ_a=0

The check on the aggregated signature will then be:

e(σa,G2)==e(H(m),pk_a)

And is:

e([0].G1,G2)==e(H(m),[0].G2)

and which will be the same as:

e([0].G1,G2)==e([0].H(m),G2)

and which will be the same as:

e([0],G2)==e([0],G2)

And so the test will pass if the zero aggregation is not checked. Eve has thus signed for a message that she does not know anything about its contents. We should thus always check for a zero value in the public key and/or in the signature, and reject them if they are zero.

An outline of the Go code is given next [here], and the aggregation part is highlighted:

package main

import (
 "bytes"
 "fmt"
 "math/big"
 "os"
 "crypto/rand"

 "github.com/cloudflare/bn256"
)

func main() {

 salt := []byte{11, 12, 13, 14}

 message:="Hello"

 argCount := len(os.Args[1:])

 if argCount > 0 {
  message = os.Args[1]
 }

 msg := []byte(message)

 G2 := new(bn256.G2).ScalarBaseMult(big.NewInt(1))

 privKey, _, _ := bn256.RandomG2(rand.Reader)
 pubKey := new(bn256.G2).ScalarBaseMult(privKey)

 hash := bn256.HashG1(msg, salt)
 sigma := new(bn256.G1).ScalarMult(hash, privKey)


 rhs := bn256.Pair(hash, pubKey)
 lhs := bn256.Pair(sigma, G2)

 fmt.Printf("Message: %s\n", message)
 fmt.Printf("Private key 1: %x\n", privKey)
 fmt.Printf("\nPublic key 1: %x\n", pubKey.Marshal())
 fmt.Printf("\nSignature (sigma): %x\n", sigma.Marshal())

 if bytes.Equal(rhs.Marshal(), lhs.Marshal()) {
  fmt.Printf("\nSignature verified!\n")
 }

 betapubKey:= new(bn256.G2).ScalarBaseMult(privKey)

 betapubKey.Neg(betapubKey)
 pub_aggr := pubKey.Add(pubKey, betapubKey)

 
 sigma2 := new(bn256.G1).ScalarMult(hash, privKey)
 sigma2.Neg(sigma2)
 sigma_aggr :=sigma.Add(sigma, sigma2)


 fmt.Printf("Private key 2: %x\n", privKey)
 fmt.Printf("\nPublic key 2: %x\n", betapubKey.Marshal())
 fmt.Printf("\nSignature (sigma2): %x\n", sigma2.Marshal())

 fmt.Printf("\nSignature aggregated: %x\n", sigma_aggr.Marshal())
 fmt.Printf("\nPublic key aggregated: %x\n", pub_aggr.Marshal())

 rhs = bn256.Pair(hash, pub_aggr)
 lhs = bn256.Pair(sigma_aggr, G2)

 if bytes.Equal(rhs.Marshal(), lhs.Marshal()) {
  fmt.Printf("\nAggregated Signature verified!")
 }

}

A sample run is [here]. Notice that the aggregated public key and signature values have been set to zero:

Message: abc
Private key 1: 896c9dcfea9659ea00bfc1ddd97c98271febc873119babd25d25de4ac46968b8Public key 1: 01026c76c9a917726c83f8748301e39bb34553b59f1877281085cafae9e2ea9499837e91ef55b8f7657ce38bec5c343213f43b96385ad78fbcc298484d1f8aab3e3dbef72f2a43420435239aaca8f34557e616988413df15cf60cc12fc94b867824905b9d1d61c7bb51d593f149ffba192a84ecbc55624b6b6bb8120be579a081aSignature (sigma): 48385fd0e9f6b1a97ddc1a408bad6e806bae49b13121d84a0e07d5d4ec59fb8c325bb417ef4ca540488577ac061445dfb073ce4a698754e3d12c8801593be09fSignature verified!
Private key 2: 896c9dcfea9659ea00bfc1ddd97c98271febc873119babd25d25de4ac46968b8Public key 2: 01026c76c9a917726c83f8748301e39bb34553b59f1877281085cafae9e2ea9499837e91ef55b8f7657ce38bec5c343213f43b96385ad78fbcc298484d1f8aab3e51f60ab4206045f5754c520bb89196ca0844f04d0cd69fceb790996fc9502ee546af481174870c448d16ada3c1893a8f460cbd0bca90fee75cdb8bae066e8e4dSignature (sigma2): 48385fd0e9f6b1a97ddc1a408bad6e806bae49b13121d84a0e07d5d4ec59fb8c5d594dcb5b56e2b961ea750c5b7096423de7ba86b72e60ba4730246b04ccb5c8Signature aggregated: 00000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000Public key aggregated: 00Aggregated Signature verified!

We can see that Eve has taken Bob’s public key, and has no idea about the message she is signing. She then creates a negative value of his value and passes that with the negative value of the signature. When Trent checks the signature, it looks like both Bob and Eve have signed for the message. Perhaps this might be to transfer some cryptocurrency from Bob to Eve?

Conclusions

And, so, watch out for that pesky zero value. It is there, and can’t be ignored!