Would You Take On A $1 Million Bet For The Cracking of Elliptic Curve Cryptography (ECC) By 2050?

Would You Take On A $1 Million Bet For The Cracking of Elliptic Curve Cryptography (ECC) By 2050?
There is a great deal of debate about the cracking of public key encryption with Quantum Computers. Like it or not, Shor’s algorithm [3] showed how we can crack RSA, Elliptic Curves Cryptography (ECC) and Discrete Logarithms using Quantum Computers. The theory is unquestionable, but the time that QCs will be built for production-level cracking is the main question to be answered — or at least, proposed.
And, so, on 18 April 2023, a strange challenge was posted to the PQC email forum:

It was from John Preuß Mattsson from Ericsson Research:

The bet follows one made in 2017 between Daniel J Bernstein (djb) and Francisco Rodríguez-Henríquez, and where RSA-2048 will be cracked by 2033. John’s bet of $2,050 is that RSA-2024 will not be cracked by 2050. Again, djb stood the bet, along with John Sahhar, Daniel Apon, and Michele Mosca. John Sahhar, in fact, posted a further challenge that wagered $1 million that 256-bit Elliptic Curve methods would be broken by 2050:
On Tuesday, April 18, 2023, John Sahhar <jo...@entropy.xyz> wrote:
Hello John,
Wager accepted.
Furthermore, I wager anyone 1,000,000$ USD that solving the discrete logarithm
of any 256 bit Elliptic Curve will be computationally feasible by a
quantum computer before or during the year 2050.
Any takers?
--
Regards,
John Sahhar
Cryptographer @ Entropy Cryptography Services, Inc.
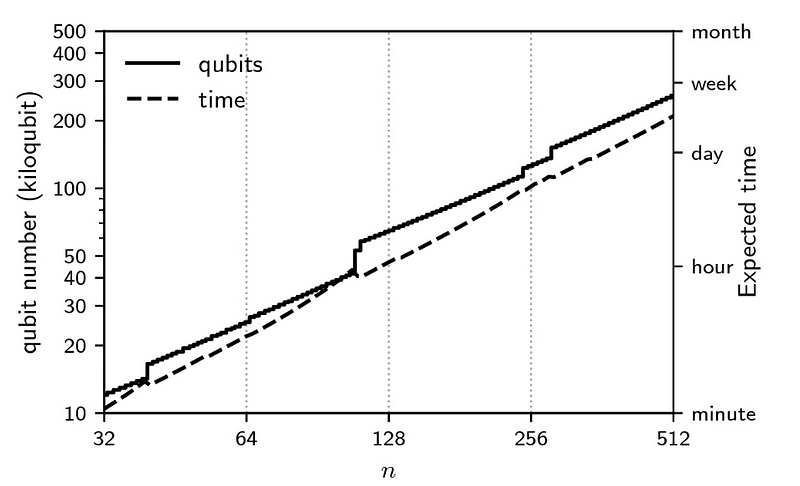
Contact - https://ok-john.us/aboutFor this, Gouzien et al [4] recently computed the expected time to crack an n-bit ECC problem for the number of kiloqubits, and found that ECC-256 could be crackable within 100 kiloqubits:
RSA
RSA gains its key security strength from the multiplication of two prime numbers (p and q) to get N. If we get p and q, then we can work out:
Phi = (p-1)(q-1)And since we have encryption key (e), which is normally 65,537, we solve for d in:
d x e mod (PHI) = 1Basically we have the inverse of e mod PHI For example, if we have an e value of 65,537 and a PHI of 10,347,768,518,374,182,260, then the decryption key value (d) will be 12,406,113,933,120,080 Test.
And so, it becomes easy to crack RSA if we can crack N. But when we define that a digital certificate has 2,048 bits, how big are the values of p and q? Well, if we have an n bit value and multiply it with an m-bit value, we get a result which has n+m bits. And so if our RSA keys are 2,048 bits long, then our prime numbers will be half this size (1,024 bits).
So how many digits will a 1,204-bit have? Well, we can use Python to determine that it has 309 digits:
>>> y=2**1024
>>> print y,len(str(y))
1797693134862315907729305190789024733617976978942306572734300811577326758055
0096313270847732240753602112011387987139335765878976881441662249284743063947
4124377767893424865485276302219601246094119453082952085005768838150682342462
8814739131105408272371633505106845862982399472459384797163048353563296242241
37216 309and when we multiply two 1,024-bit primes, we get a 617-digit number:
>>> y=2**2048
>>> print y,len(str(y))
3231700607131100730071487668866995196044410266971548403213034542752465513886
7890893197201411522913463688717960921898019494119559150490921095088152386448
2831206308773673009960917501977503896521067960576383840675682767922186426197
5616183809433847617047058164585203630504288757589154106580860755239912393038
5521914333389668342420684974786564569494856176035326322058077805659331026192
7084603141502585928641771167259436037184618573575983511523016459044036976132
3328723122712568471082020972515710172693132346967854258065669793504599726835
2998638215525166389437335543602135433229604645318478604952148193555853611059
596230656 617Martin Gardner’s Scientific American column first proposed the RSA method; the challenge was to break an N value of just 129 digits, and which would be fairly easy to crack today (but at the time, Ron Rivest thought it would take 40 quadrillion years to factorize).
So if we want to generate two prime numbers, how long will it take? Well again, we can turn to Python and use the Riemannr method to estimate the number of prime numbers that are 1,024 bits long:
import sys
import math
from mpmath import *
start=2**1023
end=2**1024
n=int(riemannr(end))-int(riemannr(start))
print "Est prime numbers :\t",n
print "Estimation to find is 1 in",(2**1024)/nIf we run, we determine that we have a massive number for1,024-bit numbers, but that the chances of us finding one is 1-in-1,418:
Est prime numbers : 12669164489297035838042749092693935645472324718849614339
24766525026995310075958371294812932404687423824670251209
13518137109729182502216808596722503552506608383945568062
99217183402234779768002807879623065822080202513999439628
97095578902630452877769836056051748736023462240653644712
9531599628766639300804608
Estimation to find is 1 in 1418And so we could generate a 1,024-bit number using a getranbits() function:
>>> import random
>>> random.getrandbits(1024)
15654893957198661793659339869648762626928106936154995487229066495551436156
60284302283936904605999192255617800896341580115876142806669637546683257799
87475479846196199822356717682549864936396590068357782045162223432591023551
79921479423328121602635499342863552800705402228884739261770997781684685099
2096404056283L
>>> random.getrandbits(1024)
55136965950425835689158416465806396636650650968403266989581732336809191724
27568382862185929570643407015110118361425841640303197239787014076897450410
98267573419642505656979080087526916229307695938956295995343564916977819109
73306456605765264018712506188755530370692209478031117756834222205525907403
426552222412LAnd then test if it is a prime number. If not, we decrement it and test again. From our calculation, it should only take 1,418 attempts to find one.
Factorization
One of the most popular methods of factorizing a modulus is the prime sieve. This can create all the prime numbers up to a given limit. For this, it progressively removes composite numbers until it only has prime numbers left, and it is the most efficient way to generate a range of prime numbers [here]:
import sys
test=1000
if (len(sys.argv)>1):
test=int(sys.argv[1])
def sieve_for_primes_to(n):
size = n//2
sieve = [1]*size
limit = int(n**0.5)
for i in range(1,limit):
if sieve[i]:
val = 2*i+1
tmp = ((size-1) - i)//val
sieve[i+val::val] = [0]*tmp
return [2] + [i*2+1 for i, v in enumerate(sieve) if v and i>0]
print (sieve_for_primes_to(test))This works because we start with all the odd numbers up to the square root of the limit of the numbers we are looking for. If we have 100, then the size will be 50. We start off with odd numbers (as 2 is the only even prime):
3 5 7 9 11 13 15 17 19 21 23 25 27 29 31 33 35 .. 99In the first time round, we have i equal to 1, and we will jump three each time and mark them as not prime (to find all the factors of 3):
3 5 7 9 11 13 15 17 19 21 23 25 27 29 31 33 35 .. 97 99In the next time round, we will jump 5, starting at 5 (to find all the factors of 5):
3 5 7 X 11 13 X 17 19 X 23 25 X 29 31 X 35 .. 97, XIn the next time round, we will jump 7, starting at 7 (to find all the factors of 7):
3 5 7 X 11 13 X 17 19 X 23 X X 29 31 X X .. 97 99In the next time round, we will jump 9, starting at 9 (to find all the factors of 9):
3 5 7 X 11 13 X 17 19 X 23 X X 29 31 X X .. 97 99In the end, we stop at 19, and with a jump of 19, and add the value of 2 to the discovered prime numbers:
2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 37, 41, 43, 47, 53, 59, 61, 67, 71, 73, 79, 83, 89, 97In February 2020, Boudat et al cracked the RSA-250 (828-bit) RSA challenge.
RSA-250 = 2140324650240744961264423072839333563008614715144755017797754920881
41802344714013664334551909580467961099285187247091458768739626192155736304745
47705208051190564931066876915900197594056934574522305893259766974716817380693
64894699871578494975937497937
RSA-250 = 6413528947707158027879019017057738908482501474294344720811685963202
4532344630238623598752668347708737661925585694639798853367
× 333720275949781565562260106053551142279407603447675546667845209870238417292
10037080257448673296881877565718986258036932062711
It took 2700 CPU core-years to crack, and used the Number Field Sieve algorithm. At present RSA-260 (with an 862-bit modulus) is still yet to be factored.
Energy to crack RSA
In order to understand the concept of work in cracking cryptography, Lenstra [here] defined the concept of Global Security in order to show the amount of energy required to crack cryptographic algorithms and compared this with the amount of water that energy could boil something. This could be seen as the carbon footprint of cracking. For a 35-bit key symmetric key (such as AES), you only need to pay for the boiling of a teaspoon of energy, and for a 50-bit key, you just need to have enough money to pay for a shower:

So let’s look at RSA. In order to crack it, we need to factor N, into p and q (the two prime numbers used). Once cracked we can determine PHI (p-1 x q-1), and then we can determine the decryption value (d) [here]. First we will take teaspoon security, and where we would need to consume the amount of energy that can boil a teaspoon. A sample would be (242-bit RSA modulus) [here]:
N=p*q= 5896261486983538627098661478596873684661596787145726508859641645687965941The prime numbers have 121 bits, and, if we were to crack it, the prime numbers are:
(p): 2526944374765758521282783272842906989
(q): 2333356264531983395509730755656883369
Now we try pool security, which will have a 745-bit modulus [here]:
N=p*q= 328205934170686373022187747612351335632840120299170566830841570637
9188051825372906035688294891169122618349070595368602314959416566832509599
8315760949745673726122108730625118573143944403355956100353972339795087626
332085413773You would then have to consume the amount of energy to boil a swimming pool of water, in order to recover p and q, and which would be:
(p): 5136574890107321107930054184342872847511932740355863615831749987190796683508207354267329960601590388187075433061
(q): 6389587248163902409204449208538775019640799414724150251382810569000364623759594714615114512184726059299258653193
Now, for a 2048-bit modulus, we would have to get the energy to boil all the seas in the world in order to factorize this [here]:
N=p*q= 43167595701317556262423026656965675311752941263790242843723869722559
144737611460632568632166086252510023021805945735591772225470974213720757550
705733352824448503063524999506226660596906575816882736759369162417329042308
450768818539569647978275834799861395280256322795630706924323442073941650079
693323544638961692274755658766444829616155400362106306476222028695948219411
648554898625217423276610753800859051583718732195244823763757178756946886496
848799638990325775625765337088319529344897632569507945680260646306289624365
294219736449252864209416787913390862597496737460530614841627093463597005887
159713If you could afford the energy to boil all the seas on the planet, you would be able to recover the prime number factors of:
(p): 196609148217569855881469103057436778288884865730728431036496969106242709174542556226244974424242605165013577403243273721574500460326174617160923703395095978667090714867455310166651932606597318485468745721964757615177804666962624050069365974032392172635080905056653578728556376998092239415714121906067
(q): 219560463450804526512484156665207894511493329487508026519690092833541901773486924130405885017845670513121751269792879364231218578683707161192474640518621978728363979172391042793592947789410287416485864619629721775927035570271970144478351754084252110756000450203907965120369883036301470716442779209339
Finally we move to solar security (4,096-bit modulus) [here]:
N=p*q= 3960081571383420167814679941098524090937928309488590816012966209196161
59444771762982998281742614769950085835373633688668853821250073947649451843317
63127740889689913339769476982485196299914926425291200057886981310196228990512
39531916630515702854026672543263467130654985378038454931630236636653155999253
15366700074161673989825266680250596893213648402916649743292204325165627189457
37512995133742238763414737889717689596594940936603320164685586622634279597696
31314190762350433414241237989194424754061077772372503406770663167105510157438
84806364760908105004039219356874473644256410687605601259222256483418680387352
64967608079486689900423169681293757820777934203160497764745460850380219719149
74545368413754514832542993932007256348508892381012868762395242004260990250419
46627175266405264688454960117593326352185765247840328380867332936071498927419
65795390048891588911879022571307124371781531933418067634220970344836212445660
78923257429637598615691552350410659591140346748167709449018947885391433407732
87887877228360277882186941355338317509867019513250617374060166135289335105304
8344129586887687118260226198269183634491741066922963You will never find the prime numbers, but they are:
(p): 2387628035654914041578676682340635535950948791037039903330270590495501744849764207480076462162294270197243407459110192208709737698247332428053357258855955290692393471421516310661792749482905080962109692416944336517049095407867686284521225687878370847230533829287501911033500368831913293493330562838467387835530549969054109399131451846959457130413492668037089837378118350872377084885693225874836148717207853352068189405415387476462556003921350678166912349980061364631958090280213640154021116006326720158290040518790513066623093136091263566334119222952846436577451
(q): 1658583963769377603578396329705793644732710623310129654038348230711585763044092787355651332948374169988931521882298144371384733551640579147022118494636732293264604461116977329421823894181755805820089237394172033870263627093736577790369697957516336302977958796425947479274422794199973433467842572527064416348509712003954901454840352976743534063167992440103943082723957859216188269111695713462656653049479588103312185114742167076660911677070759504987871743971457634287384430572107927280368523691106585718147625665698291217102305172813935222056309427697965967221113
Cracking with quantum processors
A recent paper was published that perhaps speeds up the migration process [here][1]:

In the paper, it is quoted that:
We demonstrate the algorithm experimentally by factoring integers up to 48 bits with 10 superconducting qubits, the largest integer factored on a quantum device. We estimate that a quantum circuit with 372 physical qubits and a depth of thousands is necessary to challenge RSA-2048 using our algorithm.

The worrying part of this statement is that there are companies that are creating quantum computers that are likely to release 1,000 qubit+ processors by 2025. Previously, it was thought that RSA-2048 would need millions of physical qubits to crack it.
The paper focuses on 2K RSA cracking, but another risk would be if ECC was crackable, as this would mean that our key exchange methods (with ECDH) and digital wallets for cryptocurrency could be cracked. Obviously, the word “challenge” is a little vague, and there is no real benchmark defined about how costly it would be for a quantum computer to actually crack RSA-2048.
There are, though, some doubts about the paper, as the method is not based on Shor’s method [3], but on one defined by Peter Schnorr [1] (and which was subsequently withdrawn):

Also, sublinear does not relate to sublinear time, but to the number of Qubit circuits. No practical evaluation of the time it would take to crack the modulus is given in the paper.
Cracking with lattices
In RSA, we create a modulus (N) by multiplying two random prime numbers (p and q). If we can factorize this modulus into p and q, we easily break RSA. One of the most popular methods for factorizing a modulus is using lattice methods. This includes the LLL method and which was created by AK Lenstra, HW Lenstra, Jr., and L Lovasz in 1982. If you want to see it in operation, try here:
https://asecuritysite.com/ecc/ecd
Conclusions
The bet for RSA-2048 has been laid down, but the Elliptic Curve one is still open.
References
[1] Yan, B., Tan, Z., Wei, S., Jiang, H., Wang, W., Wang, H., … & Long, G. L. (2022). Factoring integers with sublinear resources on a superconducting quantum processor. arXiv preprint arXiv:2212.12372.
[2] Schnorr, C. P. (2021). Fast factoring integers by SVP algorithms, corrected. Cryptology ePrint Archive.
[3] Shor, P. W. (1994, November). Algorithms for quantum computation: discrete logarithms and factoring. In Proceedings 35th annual symposium on foundations of computer science (pp. 124–134). IEEE.
[4] Gouzien, É., Ruiz, D., Régent, F. M. L., Guillaud, J., & Sangouard, N. (2023). Computing 256-bit elliptic curve logarithm in 9 hours with 126133 cat qubits. arXiv preprint arXiv:2302.06639.