Cryptography Fundamentals 8 : RSA — Rivest, Shamir and Adleman

Cryptography Fundamentals 8 : RSA — Rivest, Shamir and Adleman

In August 1977, The Stranglers were in the music charts with “Something Better Change” and something really was changing, and it was something that would change the world forever. This was the month that Martin Gardner in his Scientific American column, posted a challenge of a method that has stood the test of time: RSA. It related to the work of R(ivest), A(dleman) and S(hamir) and was a puzzle on their discovery of a method which allowed two keys to be created, where one could encrypt and the other to decrypt. Their work had been based on a proposal from Whitfield Diffie and Martin Hellman on trapdoor functions that could be used to create the key pair.

In order to explain the RSA concept, Martin’s provided a background the Diffie-Hellman method for which he outlined:

Then in 1975 a new kind of cipher was proposed that radically altered the 
situation by supplying a new definition of "unbreakable." a definition that 
comes from the branch of computer science known as complexity theory. These 
new ciphers are not absolutely unbreakable in the sense of the one-time pad. 
but in practice they are unbreakable in a much stronger sense than any cipher 
previously designed for widespread use. In principle these new ciphers can 
be broken. but only by computer programs that run for millions of years!

Overall the Diffie-Hellman method has had a good run, but it has struggled in recent years to keep up with the processing power for computers, and the millions of years of running is not quite the case in the modern area, and where the original ciphers could now easily be broken with the simplest of computers within minutes.

With the RSA method, Martin Gardner outlined:

Their work supported by grants from the NSF and the Office of Naval Research. 
appears in On Digital Signatures and Public-Key Cryptosystems (Technical 
Memo 82. April. 1977) issued by the Laboratory for Computer Science 
Massachusetts Institute of Technology 545 Technology Square. Cambridge Mass. 
02139.
The memorandum is free to anyone who writes Rivest at the above address 
enclosing a self-addressed. 9-by-12-inch clasp.

On receipt the requesters eventually (it took over four months in many cases) received a precious piece of history:

It seems unbelievable these days, but the original methods were based on two 63-digit prime numbers that would be multiplied to create a 126-digit value:

Contrast this with the difficulty of finding the two prime factors of a 
125- or 126-digit number obtained by multiplying two 63-digit primes. 
If the best algorithm known and the fastest of today's computers were 
used, Rivest estimates that the running time required would be about 
40 quadrillion years'

A 256-bit number, at its maximum, generates 78-digits:

115,792,089,237,316,195,423,570,985,008,687,907,853,269,984,665, 
640,564,039,457,584,007,913,129,639,936

Web: https://asecuritysite.com/encryption/keys3

The 40 quadrillion years has not quite happened, and where 512-bit keys are easily broken in Cloud. If you are interested, here is a 512-bit integer value and which has 148 digits, such as:

13,407,807,929,942,597,099,574,024,998,205,846,127,479,365,820,592,
393,377,723,561,443,721,764,030,073,546,976,801,874,298,166,903,427,
690,031,858,186,486,050,853,753,882,811,946,569,946,433,6 49,006,084,096

web: http://asecuritysite.com/encryption/random2

The search for prime numbers, too, has been progressive since 1977, and by 2014, the world discovered a 17,425,170-digit prime number. The finding of prime numbers make the finding of them in the RSA method must easier.

So the RSA method has been under attack for years, from both discovering prime numbers and also in factorizing. Along with this computing power has increased massively. If think that 40 years that have passed, and take a quick assumption that computing power doubles every year then we get:

1977 4 Quadrillion Years (4,000,000,000,000,000)
1978 2 Quadrillion Year
1979 1 Quadrillion Year
…
2020 227 years
2021 113 years
2022 57 years
2023 28 years

and if we get a GPU card with 4,000 processors, we take it to less than a year, and we get of few of them today into a cluster, and we crack it within one day! The FREAK vulnerability was actually caused by the limiting of RSA keys, due to US Export controls, to 512-bits.

The factorising of prime numbers too has generated methods which can quickly find the prime number factors

The Tension of Crypto and Academic Freedom

Once Martin had published the article, the requests for the article came rushing in, especially as the paper had not yet appeared in the Communication of the ACM. Initially there were 4,000 requests for the paper (which rose to 7,000), and it took until December 1977 for them to be posted.

Why did it take so long to get the paper published and also to send them out? Well the RSA method caused significant problems within the US defence agencies. This was highlighted in a letter sent from J.A.Meyer to the IEEE Information Theory Group on a viewpoint that cryptography could be violating the 1954 Munitions Control Act, the Arms Export Control Act, and the International Traffic in Arms Regulations (ITAR), and could thus be viewed equivalent to nuclear weapons. In even went on to say that:

Atomic weapons and cryptography are also covered by special secrecy laws

The main focus of the letter was that any work related to cryptography would have to be cleared by the NSA before publication. In fact, the letter itself had been written by Joseph A Meyer, an employee of the NSA.

Joseph had already been embroiled in controversy with a proposal to fit a tracking device to the 20 million US citizens who had been associated with crime. The tag would then be used to monitor the location of the “subscriber”, and to detect when they broke a curfew or committed a crime. In this modern era of GPS tracking of everyone’s phones, Joseph’s dream has actually become a reality, but now everyone is monitored.

The RSA team thus had a major dilemma, as many of the requests for the paper come from outside the US. Martin Hellman, who was a co-author of the Diffie-Hellman method, had already had problems with ITAR, and even decided to present thep aper himself in 1977 at Cornell University rather than the practice of letting his PhD students present the work.

His thinking was that the court case would be lengthy, and that it would damage his PhD student’s studies (Ralph Merkle and Steve Pohlig), and so he stood up for academic freedoms. Initially the students wanted to present their work, but their families did not think it a good idea. Eventually though, Ralph and Steve stood beside Hellman on the stage to present the paper, but did not utter a word.

With this stance the cryptographers held ground, and hoped that a stated exemption on published work within ITAR would see them through. The worry, though, did delay the paper being published, and for the posting of the article. In reply to Meyer’s letter, the IEEE stood its ground on their publications being free of export licence controls, with the burden of permissions placed on the authors:

and then additional response from the IEEE saying they put in place safeguards for the publishing of material.

The scope of the impact of RSA was perhaps not quite known at the time with Len Adleman stating:

I thought this would be the least important paper my name would ever appear 
on

In fact, Adleman has said that he did not want his name on the paper, as he had done little work on it, but he did insist that his name went last. Often papers, too, have an alphabet order, and if so the method could have been known as the ARS method … not the kind of thing that you would want to say to audiences on a regular basis.

RSA

Within cryptography we typically use non-negative integer values, and perform integer operations. The challenge in public key encryption is to find a method which is computationally difficult for a computer to solve, if it does not know a given secret (normally the private key). One such problem is the difficulty in factorizing a value made up of the multiplication of two large prime numbers. In RSA, we take two large prime numbers — typically at least 512 bits long — and then multiply these together to create a modulus value, (N) (often at least 1,024 bits long). From this, we then derive a public exponent (e) and a modulus. The modulus N is thus determine by multiplying the two prime numbers (p and q):

N = p x q

The core challenge here is that it should be extremely difficult (and costly) to determine the two prime numbers which make up N. Next we select the value of our encryption key value for the public key (e). This is selected so that N and e do not share any factors: gcd(e,PHI)=1, and where

PHI = (p-1)(q-1)

This is known as Euler’s totient (toe-shent) function.

The most typically we use for e is 65,537 (0x10001). To produce a cipher (C), we convert our message into the form of an integer (M) and then use e and N to give:

C = M^e mod N

To decrypt this, we take the cipher (C), and recover the message value using the decryption exponent (d) and the modulus (N):

M = C^d mod N

To make RSA work we then need to calculate the private exponent (d) to obey:

(d x e) mod{PHI} = 1

and where phi is:

PHI = (p-1)(q-1)

We determine d by determining the inverse of e modulus phi:

d = e^{-1} \pmod {\phi}

So let’s take p=11 and q=7, and pick e of 3. N will be:

N=p.q = 77

PHI is 6x10=60

We can’t pick e of 3 or 5, so we will pick e=7. Now we compute the decryption exponent of

d = e^{-1} mod (PHI)

>>> pow(7,-1,60)
43

If we select a message of 19, we get a cipher of:

C=19⁷ (mod 77) = 68

Now to decrypt:

M= 68⁴³ (mod 77) = 19

Our public key is then (e,N) and the private key is (d,N). The usage of the (mod N) operation is the magic that makes this work. Unfortunately, the RSA method has suffered from performance issues as we have increased the size of the prime numbers used. Thus, if researchers can crack a modulus of 1,024 bits, they will factorize the two 512-bit prime numbers used. At the current time, a public modulus of 2,048 bits is recommended. So while a modulus of this size is acceptable within a powerful computer, devices which have limited CPU resources often struggle in creating the keys, and in the encryption and decryption process.

RSA Signatures

With the mathematical operations involved, RSA is hardly ever used for core encryption, as symmetric key methods are much more efficient in their implementation. But it is fairly efficient when dealing with relatively small data sizes, such as for a symmetric key (typically only 128 bits or 256 bits long). For this, Alice might protect a symmetric key with her public key, and whenever she needs to use it, she will decrypt it with her private key. Another area where we use RSA is to take a hash of a message, and then encrypt this with the private key. As the hash is relatively small (such as 128 bits, 160 bits or 256-bits), it is relatively efficient on the use of the computing resources.

Where public key encryption methods come in most use is within creating digital signatures, and where Bob can take a hash of a message, and then encrypt this hash with his private key. Alice can then also take a hash of the received message, and decrypt Bob’s encrypted hash with his public key, and compare the values produced. If they match, she determines that it was Bob who sent the message and that it has not been changed by anyone.

In Figure \ref{fig_trust03} we see that Bob has a key pair (a public key and a private key). He takes a hash of the message and encrypts with his private key, and then appends this to the message. This and then message will be encrypted by the symmetric key that Bob and Alice share (typically this is either a long-term shared key, or has just been negotiated through a hand-shake). When she receives the ciphered message, she decrypts it with the shared symmetric key, and then takes her own hash of the message. She also decrypts the encrypted hash using Bob’s public key, and then compares the hashes. As the public key and the private key work together, only the signing by Bob’s private key will reveal the hash with his public key. Alice can then tell that the message has not been changed — as the hash would change if Eve has modified it — and that it was produced by Bob (and not by Eve pretending to be Bob). Obviously, we now have a problem in how we get Bob’s public key. An important element here, is that they have to find a way for Bob to send Alice her public key in a trusted way, so that Eve cannot intercept it, and change the keys. For this, we introduce Trent, and who is trusted by Bob and Alice to prove their keys. For this Trent signs the public key of Bob with his private key, and then Alice uses Trent’s public key to prove Bob’s public key.

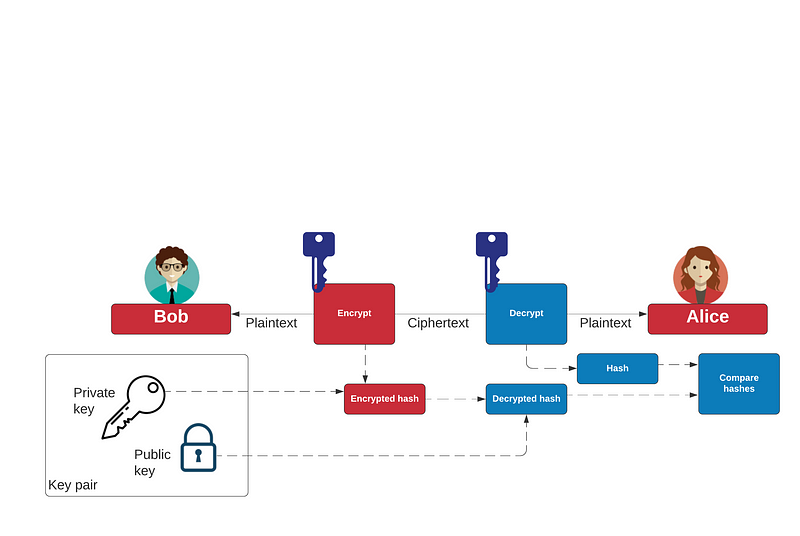
For a few decades, RSA has been the main method in supporting public key encryption. We often use it when we connect to a secure Web site, and where the RSA method is used to prove the identity of the Web site. In this case the RSA public key of the site is presented to the user in the form of a digital certificate — and which is signed by a trusted source. The Web site can then prove its identity by signing a hash of the data with its private key, and the client can check this. A typical size of the public modulus is now 2,048 bits (created by two 1,024 bit prime numbers), and with some sites supporting 4,096 bits. So while desktop computers have the processing power to cope with these large numbers, less able devices (such as for low processing powered IoT — Internet of Things — devices) will often struggle to perform the necessary calculations.

Simple example

So let’s take a simple implementation of RSA key generation, encryption and decryption. In this case the code is:

Web: https://asecuritysite.com/encryption/rsa12

In this case, we generate two random prime numbers ($p$ and $q$) for a given number of bits. The more bits we use, the more secure the method is likely to be, as an increase in the number of bits increases the number of prime numbers that can be searched for. Once we have these, we then determine the public modulus ($N$) by multiplying the prime numbers together. The difficulty of the problem is then factorizing this modulus back into the prime numbers. If we have the public modulus, it is fairly simple to then find the decryption exponent value. In most modern examples of RSA, we select a public exponent value ($e$) of 65,537, and so our encryption key becomes $(65,537,N)$. The decryption exponent ($d$) is then the inverse of $e \pmod {\phi}$ (and where $\phi=(p-1)(q-1)$).

from Crypto.Util.number import *
from Crypto import Random
import Crypto
import libnum
import sys
bits=60
msg="Hello"
p = Crypto.Util.number.getPrime(bits, randfunc=Crypto.Random.get_random_bytes)
q = Crypto.Util.number.getPrime(bits, randfunc=Crypto.Random.get_random_bytes)
n = p*q
PHI=(p-1)*(q-1)
e=65537
d=libnum.invmod(e,PHI)
## d=(gmpy2.invert(e, PHI))
m= bytes_to_long(msg.encode('utf-8'))
c=pow(m,e, n)
res=pow(c,d ,n)
print ("Message=%s\np=%s\nq=%s\n\nd=%d\ne=%d\nN=%s\n\nPrivate key (d,n)\nPublic key (e,n)\n\ncipher=%s\ndecipher=%s" % (msg,p,q,d,e,n,c,(long_to_bytes(res))))
\end{lstlisting}

A test run using 60-bit prime numbers is:

Message=hello
p=242648958288128614541925147518101769011
q=299356840913214192252590475232148200447
N=72638625604016464006874651287120524699932001616388639276131104258310920947917
cipher=5847803746095553957863305890801268831081138920772806292673259864173015661385
decipher=hello

Conclusions

RSA has been around for over 46 years, and is still going strong. It can encrypt and it can sign. While the prime numbers involved has got larger, and it needs to have padding applied, it is still one of the best public key methods around, and well used on the Web.