Byzantine Secret Share Resiliance: No Need For a Dealer When A Participant Goes Bad

Byzantine Secret Share Resiliance: No Need For a Dealer When A Participant Goes Bad
Sharing From Polynomials (x) to Bi-variate polynomials (x and y)
I am so happy that one of my next podcasts will involve Anna Lysyanskaya. One of Anna’s great collaborations was with Christian Cachin, and which created the Asynchronous Verifiable Secret Sharing (AVSS) method for secret sharing [1]:

In a secret share system, a dealer splits a secret for a number of participants. Normally we define the number of players as n, and where t participants need to come together to reconstruct the secret. But what happens when the participants detect that someone has gone bad? For this, they can use AVSS to reconstruct their shares and remove the participant from the share. Normally we would need a dealer to reconstruct the secret and reshare it again. For this, the AVSS method uses bi-variate polynomials, and allows the recovery of secret shares when a participant goes bad.
In most secret sharing schemes, we have a polynomial with one variable, such as:
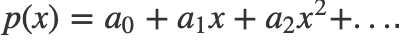
With Shamir’s Secret Shares, we store the secret share at a0, and where we distribute points on the polynomial, and then rebuild them back into a polynomial, and which should then reveal the secret.
With AVSS, we use bi-variate polynomials and which have two variables (x and y). Bi-variate polynomials are in the form of:

In this case, the secret is kept at a_00. With the Shamir method, we define a threshold (t) from a number of shares (n), and then aim to recover a polynomial f(x,y) and where the secret share is at f(0,0).
Implementation
In a typical secret sharing method, the dealer defines a polynomial of p(x)=a0+a1x+a2x2+… and where a_0 defines the secret. The dealer then sends out points on the polynomial, such for x=1 and where we have the y value of p(x=1). We can also create a commitment from the dealer so that each participant can check that their share is valid.
Within an asychronous environment, the dealer may not wait around before all the shares have been acknowledged. AVSS supports a participating party in reconstructing its share using a distributed protocol that does not require the dealer to be present. This requires f+1 participants. In asynchronous settings in which participants might fail, a dealer can wait for at most n f participants to acknowledge receiving a valid share before it inevitably may walk away. The asynchronous VSS problem requires that if the dealer (or any participant) completes the sharing protocol, then every correct participant can eventually reconstruct its share using a distributed protocol involving f+1 participants.
I have included the full theory here:
https://asecuritysite.com/shares/avss
The following code is based on the Tor.us source. In this case, we will define t for the threshold and n for the number of shares [here]:
// Based on https://github.com/torusresearch/torus-node
package main
import (
"crypto/rand"
"fmt"
"main/secp256k1"
"math/big"
"os"
"strconv"
)
func RandomBigInt() *big.Int {
randomInt, _ := rand.Int(rand.Reader, secp256k1.GeneratorOrder)
return randomInt
}
func AVSSVerifyShare(C [][]secp256k1.Point, m big.Int, sigma big.Int, sigmaprime big.Int) bool {
sG := secp256k1.BigIntToPoint(secp256k1.Curve.ScalarBaseMult(sigma.Bytes()))
rH := secp256k1.BigIntToPoint(secp256k1.Curve.ScalarMult(&secp256k1.H.X, &secp256k1.H.Y, sigmaprime.Bytes()))
sGrH := secp256k1.BigIntToPoint(secp256k1.Curve.Add(&sG.X, &sG.Y, &rH.X, &rH.Y))
pt := secp256k1.Point{X: *big.NewInt(int64(0)), Y: *big.NewInt(int64(0))}
for j := range C {
Cj0 := C[j][0]
mj := new(big.Int).Exp(&m, big.NewInt(int64(j)), secp256k1.GeneratorOrder)
Cj0mj := secp256k1.BigIntToPoint(secp256k1.Curve.ScalarMult(&Cj0.X, &Cj0.Y, mj.Bytes()))
pt = secp256k1.BigIntToPoint(secp256k1.Curve.Add(&pt.X, &pt.Y, &Cj0mj.X, &Cj0mj.Y))
}
if sGrH.X.Cmp(&pt.X) != 0 || sGrH.Y.Cmp(&pt.Y) != 0 {
return false
}
return true
}
func GenerateRandomBivariatePolynomial(secret big.Int, threshold int) [][]big.Int {
bivarPolyCoeffs := make([][]big.Int, threshold)
for j := range bivarPolyCoeffs {
bivarPolyCoeffs[j] = make([]big.Int, threshold)
for l := range bivarPolyCoeffs[j] {
if j == 0 && l == 0 {
bivarPolyCoeffs[j][l] = secret
} else {
bivarPolyCoeffs[j][l] = *RandomBigInt()
}
}
}
return bivarPolyCoeffs
}
func GetCommitmentMatrix(f [][]big.Int, fprime [][]big.Int) [][]secp256k1.Point {
threshold := len(f)
bivarPolyCommits := make([][]secp256k1.Point, threshold)
for j := range bivarPolyCommits {
bivarPolyCommits[j] = make([]secp256k1.Point, threshold)
for l := range bivarPolyCommits[j] {
gfjl := secp256k1.BigIntToPoint(secp256k1.Curve.ScalarBaseMult(f[j][l].Bytes()))
hfprimejl := secp256k1.BigIntToPoint(secp256k1.Curve.ScalarMult(
&secp256k1.H.X,
&secp256k1.H.Y,
fprime[j][l].Bytes(),
))
bivarPolyCommits[j][l] = secp256k1.BigIntToPoint(secp256k1.Curve.Add(&gfjl.X, &gfjl.Y, &hfprimejl.X, &hfprimejl.Y))
}
}
return bivarPolyCommits
}
type PrimaryPolynomial struct {
Coeff []big.Int
Threshold int
}
func PolyEval(polynomial PrimaryPolynomial, x big.Int) *big.Int {
return polyEval(polynomial, int(x.Int64()))
}
func polyEval(polynomial PrimaryPolynomial, x int) *big.Int { // get private share
xi := big.NewInt(int64(x))
sum := new(big.Int)
sum.Add(sum, &polynomial.Coeff[0])
for i := 1; i < polynomial.Threshold; i++ {
tmp := new(big.Int).Mul(xi, &polynomial.Coeff[i])
sum.Add(sum, tmp)
sum.Mod(sum, secp256k1.GeneratorOrder)
xi.Mul(xi, big.NewInt(int64(x)))
xi.Mod(xi, secp256k1.GeneratorOrder)
}
return sum
}
func EvaluateBivarPolyAtX(bivarPoly [][]big.Int, index big.Int) PrimaryPolynomial {
fiY := PrimaryPolynomial{
Coeff: make([]big.Int, len(bivarPoly)),
Threshold: len(bivarPoly),
}
for l := range bivarPoly[0] { // loop through horizontally first
for j := range bivarPoly { // loop through vertically
fiY.Coeff[l] = *new(big.Int).Add(
&fiY.Coeff[l],
new(big.Int).Mul(
&bivarPoly[j][l],
new(big.Int).Exp(&index, big.NewInt(int64(j)), secp256k1.GeneratorOrder),
),
)
}
}
return fiY
}
func EvaluateBivarPolyAtY(bivarPoly [][]big.Int, index big.Int) PrimaryPolynomial {
fiX := PrimaryPolynomial{
Coeff: make([]big.Int, len(bivarPoly)),
Threshold: len(bivarPoly),
}
for j := range bivarPoly { // loop through vertically first
for l := range bivarPoly[j] { // loop through horizontally
fiX.Coeff[j] = *new(big.Int).Add(
&fiX.Coeff[j],
new(big.Int).Mul(
&bivarPoly[j][l],
new(big.Int).Exp(&index, big.NewInt(int64(l)), secp256k1.GeneratorOrder),
),
)
}
}
return fiX
}
func showMatrix(msg string, m [][]big.Int, size int) {
fmt.Printf("%s\n", msg)
for i := 0; i < size; i++ {
fmt.Printf("Row: ")
for j := 0; j < size; j++ {
fmt.Printf("%s ", m[i][j].String())
}
fmt.Printf("\n")
}
fmt.Printf("\n")
}
func showPoints(msg string, m [][]secp256k1.Point, size int) {
fmt.Printf("%s\n", msg)
for i := 0; i < size; i++ {
fmt.Printf("Row: ")
for j := 0; j < size; j++ {
fmt.Printf("%s ", m[i][j].X.String())
}
fmt.Printf("\n")
}
fmt.Printf("\n")
}
func main() {
threshold := 3
s := 5
nodes := 5
// secret := *RandomBigInt()
argCount := len(os.Args[1:])
if argCount > 0 {
s, _ = strconv.Atoi(os.Args[1])
}
if argCount > 1 {
threshold, _ = strconv.Atoi(os.Args[2])
}
if argCount > 2 {
nodes, _ = strconv.Atoi(os.Args[3])
}
secret := *big.NewInt(int64(s))
fmt.Printf("Secret=%d, threshold=%d, nodes=%d\n", s, threshold, nodes)
f := GenerateRandomBivariatePolynomial(secret, threshold)
showMatrix("=== Show f (share at f(0,0))===", f, threshold)
fprime := GenerateRandomBivariatePolynomial(*RandomBigInt(), threshold)
showMatrix("=== Show f' ===", fprime, threshold)
C := GetCommitmentMatrix(f, fprime)
showPoints("=== Show Commitments (C - X points) ===", C, threshold)
sigma := polyEval(EvaluateBivarPolyAtX(f, *big.NewInt(int64(threshold))), 0)
sigmaprime := polyEval(EvaluateBivarPolyAtX(fprime, *big.NewInt(int64(threshold))), 0)
fmt.Printf("\n1st share: Sigma=%s, Sigma_p=%s", sigma, sigmaprime)
rtn := AVSSVerifyShare(C, *big.NewInt(int64(threshold)), *sigma, *sigmaprime)
fmt.Printf("\nVerified share: %v ", rtn)
/*
for node := 0; node < nodes; node++ {
i := *big.NewInt(int64(node + 1))
AIY := EvaluateBivarPolyAtX(f, i)
AIprimeY := EvaluateBivarPolyAtX(fprime, i)
BIX := EvaluateBivarPolyAtY(f, i)
BIprimeX := EvaluateBivarPolyAtY(fprime, i)
fmt.Printf("AIY=%v, AIprimeY=%v, BIX=%v, BIPrimeX=%v\n", AIY.Coeff, AIprimeY.Coeff, BIX.Coeff, BIprimeX.Coeff)
} */
}A sample run [here]:
Secret=5, threshold=3, nodes=5
=== Show f (share at f(0,0))===
Row: 5 9743195669945784265736128598508718513383431809992852931467201572222501709532 11921601245529184890572677981314550793638440277120977934507285858736284872764
Row: 38914775169750618295866116389646254021539712841774945361261041297120280450770 39728712398652269566024872460140072549594041362028713476440569412633907719597 93804328507791152440549289202239599104421824368912194876844146484734559224879
Row: 29699601562624258681390881187189276130152510632542564550139048371246796426949 20177829835342526168771993908034295528249900168488246059089443608353861373117 50725914710115279957671906851075719555745896639024880177910113896553695516565
=== Show f' ===
Row: 115470196996176989345349889981956268662981937404082398634901967695935968192584 33044579844575268229918544233776696118670553243354949460102752276645043035280 94715233694196754547344213678075119784007634903399571068809848072191720921783
Row: 4340250202862599175210727375498478088765750740690216946430308017593134758098 36851108627021186689738145561635749516393072041227168049762415989053802072740 85484825408312771819133941960259191534837442943831567555553302176157039053809
Row: 92533102775313911545179309541127851019948561944739879791724032538117151496081 65933151131078972969485082821058756347303210836121412732507767307017160267569 86168717839084739660292482381227107627026797065820199045141906676115087565692
=== Show Commitments (C) ===
Row: 115470196996176989345349889981956268662981937404082398634901967695935968192584 33044579844575268229918544233776696118670553243354949460102752276645043035280 94715233694196754547344213678075119784007634903399571068809848072191720921783
Row: 4340250202862599175210727375498478088765750740690216946430308017593134758098 36851108627021186689738145561635749516393072041227168049762415989053802072740 85484825408312771819133941960259191534837442943831567555553302176157039053809
Row: 92533102775313911545179309541127851019948561944739879791724032538117151496081 65933151131078972969485082821058756347303210836121412732507767307017160267569 86168717839084739660292482381227107627026797065820199045141906676115087565692
Sigma=36664471860921596749403324827578523677479041380983203887219069808027524711845, Sigma_p=34952158684060427389027977909099099286115732896212732538867879459624443976911
Verified share: true Conclusions
And, so, when we want to regenerate the secret share when there is a bad participant, we would have to get a dealer to gather the shares back, and then recreate the share. New shares will then be dealt out without the bad participant. This risks the dealer leaking the secret. With AVSS, the participants can get together, and recreate the secret without the bad participant.