Cryptography Fundamentals: Commutative Encryption

Cryptography Fundamentals: Commutative Encryption
What’s at the core of cryptography? Well, the simple EX-OR holds a special place, as we can do not lose any information when we apply it. For a bitwise operation of 0 EXOR 0 gives 0, 0 EXOR 1 gives 1, 1 EXOR 0 gives 1, and 1 EXOR 1 gives 0.
And, so, cryptographers dream of the perfect cipher. And that cipher is a one-time pad. Basically, we generate a one-time use key for our plaintext, and then EX-OR them together, and then just EX-OR again with the same key and we will get our plaintext back. Unfortunately, we can only use it once and need to generate another one. So, let’s see if we can generate something similar but just use the simple XOR method for our encryption and decryption.
In the Tor (The Onion Router) network, data is encrypted with a key from each of the Tor routing nodes. Thus, if we have three nodes of A, B and C, with A as the entry node and C as the exit node. For this, the user will generate a separate key for each node to use and encrypt with the key of A, then the key of B, and then the key of C. The encrypted data is passed to A, and which will decrypt with its key, and pass the encrypted data onto B, and who will decrypt with its key. Finally, C will decrypt with its key, and the data will be decrypted. This protects the data as it is routed. But we have to remove the keys in the reverse order they were applied. One way to do this is with commutative encryption.
Using a hasp
When I worked as an electrical engineer, we had a hasp to isolate the electric power on a device we were working on:

With this, each person who was working on the equipment, would put on their own padlock, and where we could not put the power back on, until all the padlocks had been taken off. The padlocks could be put on in any order, and taken off in any order, but there was no way to putting the power back on, until everyone had taken their padlock off.
So how could we do this with data. Let’s say that Bob, Alice and Carol want to apply their “data hasp”, so that the data cannot be revealed until they have all taken off their padlock. Well, with symmetric key block ciphers, such as AES, we cannot do this, as we must decrypt in the reverse order of they keys being applied:
To encrypt: Bob → Alice → Carol … and then to decrypt: Carol → Alice →Bob
There are ways to do it with RSA, such as with SRA [here], but these methods significantly reduce the security of the process. The solution is to use a stream cipher, as we basically just X-OR the data when we are encrypting, and then X-OR again with the same key when we decrypt. We can apply multiple keys to the data, and in any order and it will always decrypt properly once we have applied all the keys.
What we need with commutative encryption is to have an encryption string which is the same length as the data string. To make the encryption string, we can use an XOF (eXtendable-Output Functions) and where we can create a hash value of a given size. For this, rather than the fixed hash of SHA-3, we can use the SHAKE. Or with With BLAKE2b we have an XOF of BLAKE2XB, and for BLAKE2s we have an XOF of BLAKE2XS. We can then basically have a secret passphrase, and which generates an output which matches the length of the plaintext. Another method we can use, is to generate an pseudo infinitely long encryption key which is the same length as the plaintext — in the same way that a stream cipher works.
A simple application: Booking a ticket
With the ever increasing number of breaches, we are moving to a world where companies should not hold any personally sensitive information, as it is just too risky. So how could we create a trustworthy system, where someone can show up with a ticket, and where we can trust it, without actually revealing any personal information about where the person has booked their seat?
So how can we generate a receipt of the booking, but not give away your identity, or the details of the booking? Let’s take an example of booking a seat in a theatre at the festival, and how your privacy can be respected, but where the theatre will trust the ticket.
Let’s say there are 100 seats in a theatre, and I want to book one of them, but I don’t want the theatre company to know which seat I’ve booked, or my identity. I also want a receipt of purchase that they can verify my booking. One way would be to get a trusted agent to look after the bookings, but I don’t trust them either. So how can we do this?
Well it can be done with commutative encryption.
The steps would be:
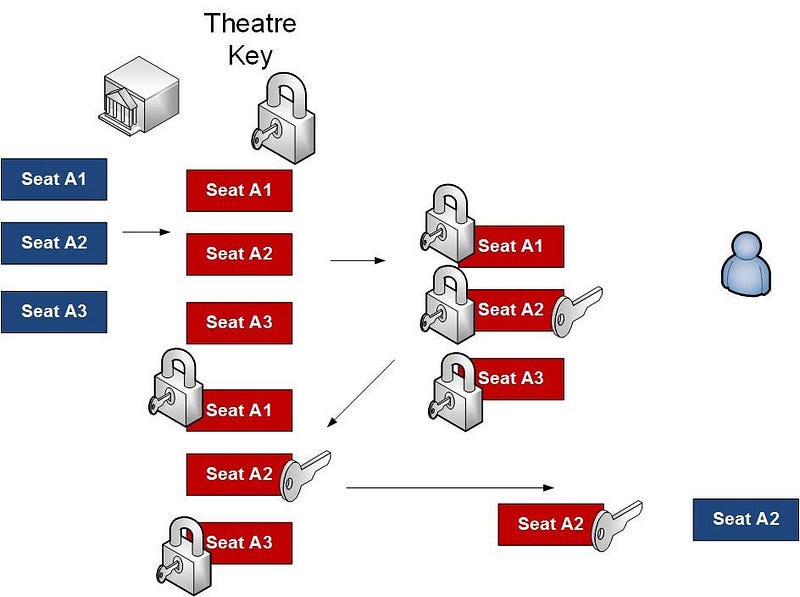
- Initially the theatre company generates 100 receipts for each of the seats, and then encrypts them with its public key.
- Next when I want to make a booking they send me the encrypted receipts that they have left, and I select one at random, and then encrypt it with my public key.
- I send them all back, including the one I’ve encrypted.
- The theatre checks to see which one has been changed, and then decrypts it with its private key, and sends it back to me.
- I decrypt with my private key, and I can now view the receipt for my booking, and the theater company cannot determine which seat I have, but I will have the receipt of my booking.
So here is an example where the theatre encrypts all the seats with its key, the person then selects one, and encrypts with their key, and sends them all back again. Then the theater decrypts the one that has changed, and sends it back for the person to decrypt, and we have a booking. The theatre thus does not know who has booked the seat:
Commutative encryption using ChaCha20
ChaCha20 is a stream cipher, and where we created pseudo infinitely long encryption key, and the just XOR it with the plain text.
With commutative encryption, we can decrypt with the keys in any order. Normally we would encrypt with Bob’s key and then encrypt with Alice’s key, and then we must decrypt with Alice’s key and then Bob’s. In commutative encryption, we can decrypt in any order.
With a stream cipher, we can automatically apply commutative as we basically just EX-OR with the key stream. In the following we use Go code, and where Bob encrypts, Alice encrypts, Bob decrypts, and then Alice decrypts [here].
And a sample run [here]:
Input text: Hello
Bob passphrase: qwerty
Alice passphrase: 123456Input text: Hello
Bob keygen: 65e84be33532fb784c48129675f9eff3a682b27168c0ea744b2cf58ee02337c5
Alice keygen: 8d969eef6ecad3c29a3a629280e686cf0c3f5d5a86aff3ca12020c923adc6c92Cipher after Bob encrypt: d9eef8ecdc
Cipher after Alice encrypt: 7a5dcd0f43
Cipher after Bob decrypt: ebd6598ff0
Cipher after Alice decrypt: 48656c6c6f
Decrypted text: HelloWe can easily extend the method to Carol, Trent, and so on. In my simple example I have used the same nonce for Bob and Alice, but in real life they would use different values, and these would be random for every transaction.
Commutative encryption using SHAKE-128
NIST chose Keccak as the standard for SHA-3. But, it’s all a bit confusing, as there are two main versions of this: Keccak and SHA-3. Many systems, such as Ethereum have adopted Keccak, while others go for SHA-3. The only real difference between them is a difference in the padding of data. An eXtendable-Output Function (XOF) produces a bit string that can be of any length. In fact, we can create an infinitely long bit string, if required. The main methods are SHAKE128, SHAKE256, BLAKE2XB and BLAKE2XS. With the SHA-3 hashing method, we have four different cryptographic hashing methods (SHA3–224, SHA3–256, SHA3–384, and SHA3–512) and two XOF functions (SHAKE128 and SHAKE256).
With commutative encryption, we can decrypt with the keys in any order. Normally we would encrypt with Bob’s key and then encrypt with Alice’s key, and then we must decrypt with Alice’s key and then Bob’s. In commutative encryption, we can decrypt in any order. While our symmetric key block ciphers cannot be made commutative, we can use stream ciphers, as they perform an EX-OR function. In this example we will use the SHAKE128 or SHAKE256, and generate Bob and Alice’s key.
https://asecuritysite.com/commul/comm_stream
Communicative encryption using SRA
With maths, operators such as multiplication are commutative, such as:
3 x 5 x 4 = 4 x 5 x 3In encryption, most operations are non-commutative, so we need to modify the methods. One way is to use RSA, but generate two keys which have shared p, q and N values. So we generate Bob and Alice’s keys using the same two prime numbers (p and q), so that they share the same N value (modulus).
So let’s start with Bob:
Let’s select: P=7, Q=13The calculation of n and PHI is:
N = 7 x 13 = 91PHI = (P-1)(Q-1) = 72
We need to make sure that our encryption key (e) does not share any factors with PHI (gcd(PHI,e)=1). We can select e as:
e = 5Next we can calculate d from:
(d x 5) mod (72) = 1The answer is 29 [Solve]
d= 29, e=5, N=91
Encryption key [91,5]
Decryption key [91,29]Now for Alice. We have:
N = 7 x 13 = 91
PHI = (P-1)(Q-1) = 72We can select e as (and should not share any factors with PHI):
e = 7Now we must solve:
(7 x d) mod (72) = 1For this we get 31 [Solve]
Alice’s keys are then:
d= 31, e=7, N=91
Encryption key [91,7]
Decryption key [91,31]An example of this is here:
https://asecuritysite.com/commul/comm2
Commutative encryption using Massey-Omura
As we have seen, commutative encryption allows us to decrypt in any order. For this we can use Massey–Omura Cryptosystem and generate encryption keys which share a prime number.
One classic patent for commutative encryption was written by James Massey and Jim K. Omura created the Massey–Omura Cryptosystem in 1982 [1]. It took over three years to be assigned and was assigned to Omnet Associates [here]:

It uses exponentiation in the Galois field GF(2^n) for both the encryption and decryption functions. In this, if we have a message of M, the encryption is:

and

This are operated on with the Galois field. For this we define e within:

and we make sure that e does not share a factor with 2^n-1 using:

The decryption exponent d is defined as:

This works because the multiplicative group of the Galois field GF(2^n) has order 2^n−1, and where Lagrange’s theorem defines that m^{de}=m for all the values of m in GF(2^n). The coding is here [link]:
import libnum
import random
import sysfrom Crypto.Util.number import getPrime
from Crypto.Random import get_random_bytes
def chunkstring(string, length):
return (string[0+i:length+i] for i in range(0, len(string), length))
def generate_keys(prime):
while True:
e = random.randint(0, prime-2)
if libnum.gcd(e, prime-1) == 1 and e > 2:
break
d = libnum.invmod(e, prime-1) return e,ddef crypt(chunk, key,prime ):
num = 0
for c in chunk:
num *= 256
num += ord(c)
res = pow(num, key, prime)
vect = []
for i in range(0, len(chunk)):
vect.append(chr(res%256))
res = res // 256 return "".join(reversed(vect))primebits=64
msg = "HellHe"if (len(sys.argv)>1):
primebits=int(sys.argv[1])
if (len(sys.argv)>2):
msg=(sys.argv[2])
FRAGMENT_SIZE = primebits//8
msg = msg + " "*((FRAGMENT_SIZE - (len(msg)%FRAGMENT_SIZE))%FRAGMENT_SIZE)res=chunkstring(msg,FRAGMENT_SIZE)
PRIME = getPrime(primebits, randfunc=get_random_bytes)e,d = generate_keys(PRIME)vect=[]
for elem in res:
enc=str(crypt(elem, e,PRIME))
vect.append(enc)enc="".join(vect)dec=[]
for elem in chunkstring(enc, FRAGMENT_SIZE):
dec.append(crypt(elem, d,PRIME))print (f"Msg={msg}")
print (f"e={e}, d={d}")
print("Decrypted: " + "".join(dec))A sample run is [link]:
Msg=Hello
e=16153579288865179167, d=10300837874192230633
Decrypted: HelloOne of the advantages of the Massey–Omura Cryptosystem is that we can apply commutative encryption. In this way, Bob may have keys of (e_b,d_b) and Alice has keys of (e_a,d_a). We can then apply the keys in any order, such as encrypting with e_a and then encrypting with e_b, and where we can then decrypt with d_a and then decrypt with d_b, or decrypt with d_b first and then decrypt with d_a (as we would normally do).
To encrypt:
Cipher=E(a_b,E(e_a,M))=E(e_a,E(e_b,M))
To decrypt:
E(d_b,E(d_a,Cipher))=E(d_a,E(d_b,Cipher))
Here is an example:
https://asecuritysite.com/commul/massey2
Conclusions
Communative encryption is a great way of applying multiple keys to encryption data, and then for them to be removed in any order that is required. It is a little like how data is encrypted in the Tor network, but that requires the keys to be removed in the reverse order they were applied. In a future podcast, I will explain how the Tor network works.