Finding A Base For a Hard Problem In Cybersecurity

Finding A Base For a Hard Problem In Cybersecurity
Our online security is fundamentally dependent on hard problems. Unfortunately, most of the methods used cannot be proven to be hard problems, and where the RSA method, discrete logs and elliptic curve methods will generally not be hard problems in a post-quantum computer world. But, for just now:
Y=g^x (mod p)
is generally a hard problem to find x, if we know Y, g and p (as long the prime number — p — is large enough). These days, p needs to have at least 1,024 bits to be secure, and in many cases, much more than that. But can we pick any value of g and p? Well, normally we randomly generate a number of a given size and then increment the value until we find that it is a prime number. Next, we must find a value of the generator g, that will work with this prime number.
If we have g^x (mod p) and where p is a prime number, can we find a value of g that makes sure that we get a unique output from 1 to p−1, for every value of x from 0 to p−2? This is known as the primitive root under modulo p.
First, we need the Euler Totient Function (φ(p)) and, when p is a prime number, this is:
φ(p)=p−1
Next, we find all the prime factors of φ(p). All powers are then computed as φ(p) divided by each prime factor. After this, all the powers from i=2 to p−1 are tested for:
i^{powers} (mod p)
If this is 1, then i is not a primitive root of p. If it is never 1, we return i. The basic form is:
Y=g^x (mod p)
where we have a generator value (g) and a prime number p. where we have a generator value (g) and a prime number p. If select a prime number of 7, and then select g values of 2, 3, 4 … 9, and then calculate the results we get:
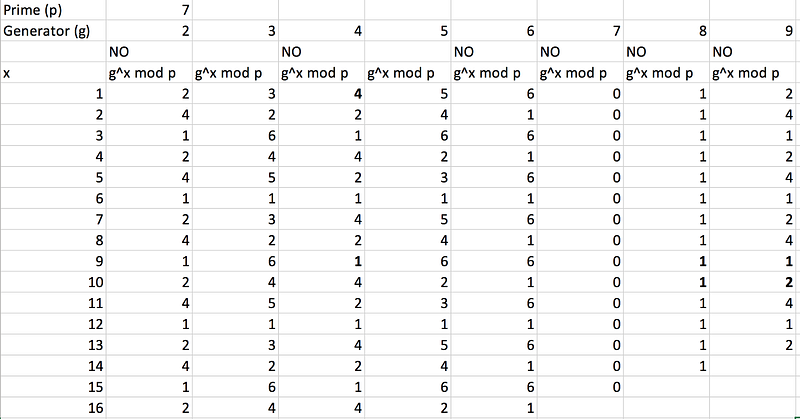
Now, look at g=2; we get an output of 2, 4, 1, 2, 4 … for the sequence values of 1, 2, … This means that we do not get a unique output for the values from 1 to 6 (where the maximum value will be six as we take the modulus of 7). But look at g=3, we get 3 (3¹(mod 7)), 2 (3²(mod 7)), 6 (3³(mod 7)), 4 (3⁴(mod 7)), 5 (3⁵(mod 7)), and 1 (3⁶(mod 7)), which means that we get a unique value for all the possible outputs from 1 to 6, and which then repeats. For a prime number of 7, the valid values of g are 3 and 5.
Some code to determine the possible powers are [here]:
import sys
def getG(p):
r = set(range(1, p))
res = []
for i in r:
gen = set()
for x in r:
gen.add(pow(i,x,p))
if gen == r:
res.append(i)
if (len(res)>10): break
return res
p=997
if (len(sys.argv)>1):
p=int(sys.argv[1])
print("Computing the first 10 generators")
g=getG(p)
print(f"p={p}")
print(f"g={g}")
print(f"\nNow trying the first 20 values for {g[0]} (there should be no repeated values):")
print(f"x\tg^x (mod p)")
print(f"===================")
for i in range(0,p):
print(f"{i}\t{pow(g[0],i,p)}")
if (i>20): breakA sample run for p=41 is [here]:
Computing the first 10 generators
p=41
g=[6, 7, 11, 12, 13, 15, 17, 19, 22, 24, 26]
Now trying the first 20 values for 6:
x g^x (mod p)
0 1
1 6
2 36
3 11
4 25
5 27
6 39
7 29
8 10
9 19In this case we see that g=6 is the first generator for p=41, but we could also use 7, 11, 12 and 13.
Generating a safe generator in OpenSSL
In OpenSSL, we can generate a random prime number of a given size, and it will create a safe generator for us. For example, to generate a 512-bit prime number:
% openssl dhparam -text -out dhparams.pem 512
Generating DH parameters, 512 bit long safe prime
...............+..............+.........................+...++*++*++*++*++*++*++*++*++*++*++*++*++*++*++*++*++*++*++*++*++*++*++*++*++*++*++*++*++*++*++*++*++*++*++*++*++*++*++*++*++*++*++*++*++*++*++*++*++*++*++*++*++*++*++*++*++*++*++*++*++*++*++*++*
% cat dhparams.pem
DH Parameters: (512 bit)
P:
00:b9:2e:60:17:90:5d:2e:dc:ef:4d:ba:33:61:13:
a5:78:09:da:e5:85:f4:ee:49:ed:4d:6f:a1:93:51:
4f:f6:39:64:ff:52:67:9f:d8:21:ea:bb:3d:d3:61:
fb:33:a1:70:ea:ee:4f:8e:b1:a1:f9:e1:ed:a3:f4:
83:7f:03:be:77
G: 2 (0x2)
-----BEGIN DH PARAMETERS-----
MEYCQQC5LmAXkF0u3O9NujNhE6V4CdrlhfTuSe1Nb6GTUU/2OWT/Umef2CHquz3T
YfszoXDq7k+OsaH54e2j9IN/A753AgEC
-----END DH PARAMETERS-----and for a 1,024 bit random prime:
% openssl dhparam -text -out dhparams.pem 1024
Generating DH parameters, 1024 bit long safe prime
....................................................+.......................................................................................................................+......................+........................................................................++*++*++*++*++*++*++*++*++*++*++*++*++*++*++*++*++*++*++*++*++*++*++*++*++*++*++*++*++*++*++*++*++*++*++*++*++*++*++*++*++*++*++*++*++*++*++*++*++*++*++*++*++*++*++*++*++*++*++*++*++*++*++*++*and which gives:
DH Parameters: (1024 bit)
P:
00:87:2b:31:4c:06:95:06:f4:70:66:8b:d4:95:b9:
fb:cb:86:f9:45:4a:8d:2e:29:c9:f2:0f:bb:9e:c1:
37:cf:e8:a4:b2:0f:93:a0:d7:9a:ed:10:81:d9:60:
60:f7:8f:e3:eb:2a:1c:80:92:45:3d:28:2b:15:85:
c5:a5:47:8e:be:38:61:a6:48:29:54:bc:bc:61:b5:
07:68:76:2b:7c:9d:ce:d6:a9:cf:87:8c:86:41:b3:
2a:1a:36:28:57:ab:d0:db:cf:82:0c:ac:0e:36:44:
5c:90:c0:b8:85:32:27:b9:07:67:6f:5d:08:0e:d1:
ee:a5:ea:42:1f:2e:76:96:67
G: 2 (0x2)
-----BEGIN DH PARAMETERS-----
MIGHAoGBAIcrMUwGlQb0cGaL1JW5+8uG+UVKjS4pyfIPu57BN8/opLIPk6DXmu0Q
gdlgYPeP4+sqHICSRT0oKxWFxaVHjr44YaZIKVS8vGG1B2h2K3ydztapz4eMhkGz
Kho2KFer0NvPggysDjZEXJDAuIUyJ7kHZ29dCA7R7qXqQh8udpZnAgEC
-----END DH PARAMETERS-----In both cases, g=2 is a safe generator for the parameters used. Overall, we use these parameters within the Diffie-Hellman key exchange method.
Conclusions
Within discrete logs, rather than finding a prime number and then a possible base, we typically select the base that we want and then test for prime numbers until we find a prime number which works. While we don’t use discrete logs much anymore, the theory of them is still used in research papers to show proofs. And, so, if you pick the wrong generator, you could be in great trouble.