The Wonderful Research of Ivan Damgård: Hashing, Homomorphic Encryption and Zero Knowledge Proofs

The Wonderful Research of Ivan Damgård: Hashing, Homomorphic Encryption and Zero Knowledge Proofs
If you are into cybersecurity, then you will know all about the MD5 hashing method. But do you know what the MD part represents? Well, it could be Message Digest, but it could also be the Merkle-Damgård (MD) construct on which MD5, SHA-1 and SHA-2 are built upon. Overall Ivan Damgård and Ralph Merke discovered it independently and published in [1]:

But Ivan Damgård has contributed to many other areas of cybersecurity, so let’s cover a few [here].
Merkle-Damgård construct: MD5, SHA-1 and SHA-2
The foundation of trust in cybersecurity is laid by the simple concept of data hashing, and where we take data and create a fixed-length hash for the data. If we cannot trust our hashing methods, we are in trouble. When we create the perfect message hash, we thus need to make sure we have:
- Collision resistance. This is where it is extremely difficult to find two messages which have the same hash. Thus we should not be able to find the has of two messages (M1, and M2) that are the same within a reasonable time: H(M1)=H(M2).
- Pre-image resistance. If we already have a hash value (h), it should be extremely difficult to find a message which will give the same hash. Thus for a given hash (h), it is difficult to find a message (M1) for H(M1)=h.
The original hash methods were often based on the Merkle-Damgård (MD) construction. With this, we create a hash function using blocks of data. Based on the MD construct, Ron Rivest created the MD5 hashing method, and it was widely adopted in the industry. It works by taking a static initialisation vector (IV) and then feeding this into a one-way function (f), along with a block of the message. We feed this output into the next stage and so on until we get to a message pad at the end:

The one-way function (f) will generally compress the data and produce fewer bits out than are fed in. Unfortunately, the MD construct has many weaknesses, and one of the most serious is the length extension attack. With this, an adversary (Eve) can take a hash for an unknown message and then add additional data to produce a new valid hash. If you are interested, here is an attack on MD:
https://asecuritysite.com/hash/lenattack
Damgård-Jurik method
Two of the major areas of developments within cybersecurity will be the usage of homomorphic encryption, and in the usage of Shamir secret sharing. With homomorphic encryption, we can encrypt values, and then operate on them with arithmetic functions (such as add, subtract and multiply), and with Shamir secret sharing, we can split secrets into shares, and then distribute them over networks. These approaches will take privacy to new levels. So let’s look at the Damgård-Jurik method [2]:

First we select two large prime numbers (p and q) and compute:

and where lcm is the least common multiple. We then select random integer g for:

We must make sure that n divides the order of g by checking the following:
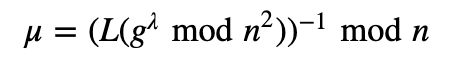
and where Lis defined as L(x)=x−1n. The public key is (n,g) and the private key is (λ,μ). To encrypt a message (M), we select a random r value and compute the ciphertext of:

and then to decrypt:
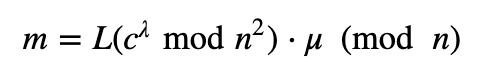
If we take two ciphers (C1 and C2), we get:

If we now multiply them we get:

And we adding two values requires a multiplication of the ciphers. If we now divide them we get:

And thus, a subtraction is equivalent to a divide operation. For this, we perform a modular divide operation. The coding is [here]:
from damgard_jurik import keygen
import sys
val_1, val_2 = 42, 12
n_b=64
if (len(sys.argv)>1):
val_1=int(sys.argv[1])
if (len(sys.argv)>2):
val_2=int(sys.argv[2])
if (len(sys.argv)>3):
n_b=int(sys.argv[3])
public_key, private_key_ring = keygen(
n_bits=n_b,
s=1,
threshold=3,
n_shares=3
)
print(f"Using Damgard-Jurik method with {n_b}-bit key, and a threshold of three and three shares\n")
print(f"Public key. n={public_key.n}, s={public_key.s}, m={public_key.m}, threshold={public_key.threshold}, delta={public_key.delta}")
c_1, c_2 = public_key.encrypt(val_1), public_key.encrypt(val_2)
c_add = c_1 + c_2
res1 = private_key_ring.decrypt(c_add)
c_sub = c_1 - c_2
res2 = private_key_ring.decrypt(c_sub)
c_mult= c_1 * val_2
res3 = private_key_ring.decrypt(c_mult)
print(f"\nval_1: {val_1}")
print(f"val_2: {val_2}")
print(f"\nc_1: {c_1.value}")
print(f"c_2: {c_2.value}")
print(f"c_1+c_2: {c_add.value}")
print(f"c_1-c_2: {c_sub.value}")
print(f"c_1*c_2: {c_mult.value}")
print(f"\nDecrypt (Add): {res1}")
print(f"Decrypt (Subtract): {res2}")
print(f"Decrypt (Multiply): {res3}")A sample run is [here]:
Using Damgard-Jurik method with 64-bit key, and a threshold of three and three shares
Public key. n=174743826971117924232203186477859825289, s=1, m=43685956742779481051423225748488060689, threshold=3, delta=6
val_1: 9
val_2: 3
c_1: 27429320619805987848765352451564237217145248338366944942206061954884249278992
c_2: 14769913771126168413630660895236067257037103416139804498830583273184880216135
c_1+c_2: 12086035254029813325315665006256800980915988130367594983597188460984693331181
c_1-c_2: 921687804424968958981627966721274246800285129994018401822135562246021703624
c_1*c_2: 21809874053261031282086634289802837387921962314468453992976726818561314427636
Decrypt (Add): 12
Decrypt (Subtract): 6
Decrypt (Multiply): 27The work on “A Generalisation, a Simplification and Some Applications of Paillier’s Probabilistic Public-Key System” received the Test of Time Award at PKC 2001.
Damgård-Fujisaki method
With the Damgård-Fujisaki method, Peggy proves to Victor that she has a positive integer value. In this case we will use the Damgard-Fujisaki method defined [here], and where Peggy has to prove to Victor that she has a positive value:

First Victor and Peggy agree on two bases for their calculations (g and h) and a prime number (n). Victor then sends Peggy using a random number (r) as a challenge. As defined by Jacobi’s four-square theorem, every positive value can be represented in the form:

For example:

Peggy now creates four commitments from these four values, and takes four random numbers (r0, r1, r2 and r3).

And:

Victor then checks:

And this should be equal to:

Coding
The following is some simple coding to prove the method. In this case we will use a prime number of 2¹⁹−1, g=3, and h=5 [here]:
import random
import sys
n=pow(2,19)-1
def lipmaa(val):
for i in range(0,100000):
for j in range(0,1000):
for k in range(0,100):
for l in range(0,10):
if (((i*i) + (j*j) + (k*k) + (l*l)) == val): return (i,j,k,l)
return(0)
x=999909
if (len(sys.argv)>1):
x=int(sys.argv[1])
if (x<0): print("Not possible to find a commitment, as negative")
sys.exit(1)
x0,x1,x2,x3=lipmaa(x)
print ("x=",x)
print (" x0,x1,x2,x3=",x0,x1, x2,x3)
g=3
h=4
r0=random.randint(0,n)
r1=random.randint(0,n)
r2=random.randint(0,n)
r3=random.randint(0,n)
r=(r0+r1+r2+r3)
c0=(pow(g,x0*x0,n) * pow(h,r0,n)) % n
print (" \nc0=",c0)
c1=(pow(g,x1*x1,n) * pow(h,r1,n)) % n
print (" c1=",c1)
c2=(pow(g,x2*x2,n) * pow(h,r2,n)) % n
print (" c2=",c2)
c3=(pow(g,x3*x3,n) * pow(h,r3,n)) % n
print (" c3=",c3)
commit1 = (c0*c1*c2*c3) % n
print (" \nCheck1=",commit1)
commit2 = (pow(g,x,n) * pow(h,r,n)) % n
print (" Check2=",commit2)
if (commit1==commit2):
print(" Peggy has proven that her value is positive")And as a test:
x= 70
x0,x1,x2,x3= 0 3 5 6
c0= 131072
c1= 422276
c2= 216515
c3= 179023
Check1= 482996
Check2= 482996
Peggy has proven that her value is positiveAnd here is a range proof:
https://asecuritysite.com/kryptology/z_df5
Conclusions
There’s something about the Danes and their love of science and mathematics … and may it always be the case. Ivan is an exceptional researcher and who laid down the core principles of hashing and, over the past two decades, has continued to contribute to many new methods.
References
[1] Damgård, I. B. (1989, August). A design principle for hash functions. In Conference on the Theory and Application of Cryptology (pp. 416–427). New York, NY: Springer New York.
[2] Damgård, I., Jurik, M., & Nielsen, J. B. (2010). A generalization of Paillier’s public-key system with applications to electronic voting. International Journal of Information Security, 9(6), 371–385.