Multivariate Cryptography Comes Storming Back for PQC

Multivariate Cryptography Comes Storming Back for PQC
Here’s my 6 am doodles from this morning on multivariate cryptography:
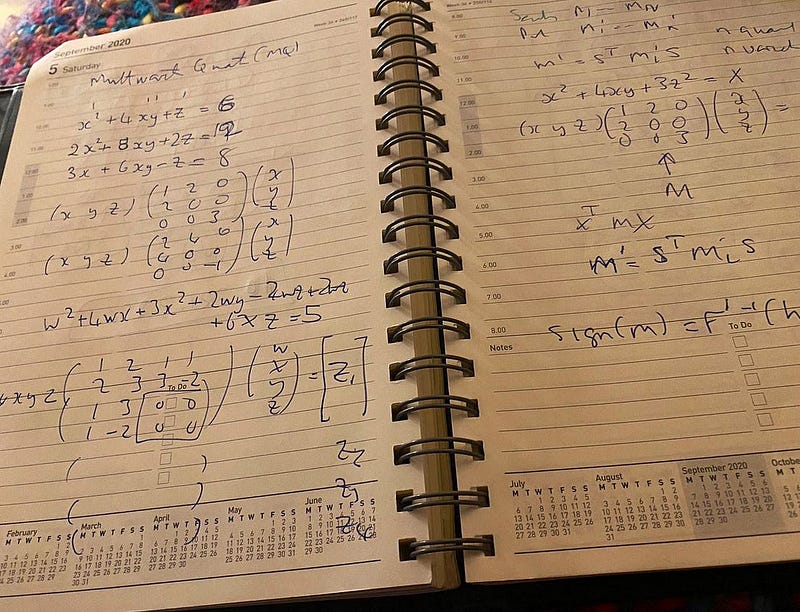
Our existing methods of public-key encryption — such as discrete logs, RSA and elliptic curve — are known not to be a hard problem in a world of quantum computers. Multivariate cryptography is a known hard problem and is robust against quantum computers. Examples of methods that use multivariate cryptography are Oil-and-Vinegar, Unbalanced Oil and Vinegar, and Rainbow. These are the latest methods that are proposed for the standardization of PQC (Post-Quantum Cryptography) signatures with Multivariate methods [here]:

Multivariate cryptography
With multivariate cryptography, we have n variables within polynomial equations. For example, if we have four variables (w, x, y, z) and an order of two, we could have [here]:
w²+4wx+3x²+2wy−4wz+2wx+6xz=387
In this case, I know that the solution is w=7, x=4, y=5, z=6. For a matrix form, we could represent this as:
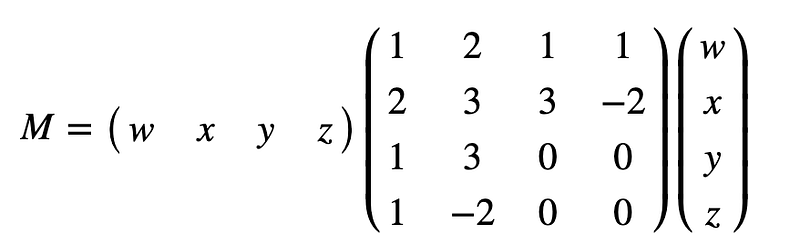
In order to constrain the values we get, we normally perform a (mod p) operation and where p is a prime number. This is known as a finite field, and our numbers are always constrained between 0 and p-1. For example, if we select p=97, we have:
w²+4wx+3x²+2wy−4wz+2wx+6xz=5 (mod 97)
Now there are multiple solutions to this now for w, x, y and z, so we define n multivariate polynomials. For example:
w²+4wx+3x²+2wy−4wz+2wx+6wx=96 (mod 97)
5w²+3wx+3x²+4wy−wz+8wx+4wx=36 (mod 97)
4w²+5wx+3x²+2wy−5wz+3wx+6wx=95 (mod 97)
6w2+7wx+4x2+2wy−8wz+2wx+9wx=17 (mod 97)
The solution to this is: w=7, x=4, y=5, z=6, but it is extremely difficult to solve, and know, and here is the code to prove this [here]:
import numpy as npp=97w=7
x=4
y=5
z=6def printM(M):
rtn = ""+str(M[0][0])+"w^2 + "+str(M[0][1]+M[1][0])+"wx + "+str(M[1][1])+"x^2 + "+str(M[0][2]+M[2][0])+"wy + "+str(M[1][3]+M[3][1])+"wz + "+str(M[0][3]+M[3][0])+"wx + "+str(M[1][2]+M[2][1])+"xz"
return rtnm=[w,x,y,z]
m_dash = np.transpose(m)
M0=[[1,2,1,1],[2,3,3,-2],[1,3,0,0],[1,-2,0,0]]
M1=[[5,2,1,2],[1,3,2,2],[3,2,0,0],[6,-3,0,0]]
M2=[[4,2,2,1],[3,3,3,-2],[0,3,0,0],[2,-3,0,0]]
M3=[[6,2,1,1],[5,4,3,-3],[1,6,0,0],[1,-5,0,0]]print ("m=",m)
print ("m^T=",m_dash)
print ("\nM0:",M0)
print ("M1:",M1)
print ("M2:",M2)
print ("M3:",M3)# res = m . M0 . m^{-1}
res1= np.dot(np.dot(m,M0),m_dash) % p
res2= np.dot(np.dot(m,M1),m_dash) % p
res3= np.dot(np.dot(m,M2),m_dash) % p
res4= np.dot(np.dot(m,M3),m_dash) % pprint ("Res0=",res1)
print ("Res1=",res2)
print ("Res2=",res3)
print ("Res2=",res4)print ()
print ()
print ("M0=",printM(M0))
print ("M1=",printM(M1))
print ("M2=",printM(M2))
print ("M3=",printM(M3))and here is a sample run [here]:
m= [7, 4, 5, 6]
m^T= [7 4 5 6]M0: [[1, 2, 1, 1], [2, 3, 3, -2], [1, 3, 0, 0], [1, -2, 0, 0]]
M1: [[5, 2, 1, 2], [1, 3, 2, 2], [3, 2, 0, 0], [6, -3, 0, 0]]
M2: [[4, 2, 2, 1], [3, 3, 3, -2], [0, 3, 0, 0], [2, -3, 0, 0]]
M3: [[6, 2, 1, 1], [5, 4, 3, -3], [1, 6, 0, 0], [1, -5, 0, 0]]M0= 1w^2 + 4wx + 3x^2 + 2wy + -4wz + 2wx + 6xz
M1= 5w^2 + 3wx + 3x^2 + 4wy + -1wz + 8wx + 4xz
M2= 4w^2 + 5wx + 3x^2 + 2wy + -5wz + 3wx + 6xz
M3= 6w^2 + 7wx + 4x^2 + 2wy + -8wz + 2wx + 9xzRes0= 96
Res1= 36
Res2= 95
Res2= 17But, what good is this in solving things? Well, in the Oil and Vinegar method, we have a special trapdoor matrix, and which allows those with secret information to have privileged access to the usage of a public key and a private key. The matrices we defined early have the trapdoors built into them:

Practical implementation
Now let’s implement the method using the code used in the submission. The following is an implementation of Rainbow Classic [here]:
#include stdio.h
#include stdint.h#include "rainbow_config.h"#include "utils.h"#include "rng.h"#include "api.h"#define MLEN 59char *showhex(uint8_t a[], int size) ;char *showhex(uint8_t a[], int size) {
char *s = malloc(size * 2 + 1); for (int i = 0; i < size; i++)
sprintf(s + i * 2, "%02x", a[i]); return(s);
}int main(void)
{
size_t i, j;
int ret;
size_t mlen, smlen;
uint8_t b;
uint8_t m[MLEN + CRYPTO_BYTES];
uint8_t m2[MLEN + CRYPTO_BYTES];
uint8_t sm[MLEN + CRYPTO_BYTES];
uint8_t pk[CRYPTO_PUBLICKEYBYTES];
uint8_t sk[CRYPTO_SECRETKEYBYTES];
randombytes(m, MLEN); crypto_sign_keypair(pk, sk);
crypto_sign(sm, &smlen, m, MLEN, sk);
ret = crypto_sign_open(m2, &mlen, sm, smlen, pk); if(ret) {
fprintf(stderr, "Verification failed\n");
return -1;
}
if(smlen != MLEN + CRYPTO_BYTES) {
fprintf(stderr, "Signed message lengths wrong\n");
return -1;
}
if(mlen != MLEN) {
fprintf(stderr, "Message lengths wrong\n");
return -1;
}
for(j = 0; j < MLEN; ++j) {
if(m2[j] != m[j]) {
fprintf(stderr, "Messages don't match\n");
return -1;
}
}
randombytes((uint8_t *)&j, sizeof(j));
do {
randombytes(&b, 1);
} while(!b);
sm[j % (MLEN + CRYPTO_BYTES)] += b;
ret = crypto_sign_open(m2, &mlen, sm, smlen, pk);
if(!ret) {
fprintf(stderr, "Trivial forgeries possible\n");
return -1;
}
printf("CRYPTO_PUBLICKEYBYTES = %d\n", CRYPTO_PUBLICKEYBYTES);
printf("CRYPTO_SECRETKEYBYTES = %d\n", CRYPTO_SECRETKEYBYTES);
printf("CRYPTO_BYTES = %d\n", CRYPTO_BYTES);
printf("Signature Length = %d\n", smlen); printf("\nAlice Public key (only showing 1/512 of key): %s\n",showhex(pk,CRYPTO_PUBLICKEYBYTES/512));
printf("Alice Secret key (only showing 1/512 of key): %s\n",showhex(pk,CRYPTO_SECRETKEYBYTES/512)); printf("\nMessage: %s\n",showhex(m,MLEN));
printf("Signature : %s\n",showhex(sm,smlen)); printf("Verfied : %d\n",r);
return 0;
}A sample run of Rainbow Classic shows that the public key size is 161,600 bytes, the secret key is 103,648 bytes, and the digital signature of 125 bytes [here]:
CRYPTO_PUBLICKEYBYTES = 161600
CRYPTO_SECRETKEYBYTES = 103648
CRYPTO_BYTES = 66
Signature Length = 125Alice Public key (only showing 1/512 of key): 7d3c1209d179008b11100d9674cb57474df22f356eaed1c28aa9da775a21b04b941654120768d8c02b0ec86480b00c97d044539677c9e67935d41c931ae77ed80a13ee4a734747b49bcfc2f9a76028d66a68ba69a2f48750ff3c7d830f8a1b545a9b9f0cc549b8601d02a8cebdb751c2525a5ddf5a928b34df01e114d74ae850a25d4ee4c5df7eb45ed23de1720961a75d01bcad44872be1d5f81e2e430ff77c1cbbc019507c0dae5702722ac4fb09681a328023d26852e0866b9808b0703de7ba89f0e6cbacff9edf9cbed446401c0724cf358878c3137dce0b48fa7bee9ff6132a6291ca030fbc1cc805f06a5d32fa2a1311afc44c0be748f0e955eba55ee06b536489f18240b2fba967ff6409227def9d496dc67eb3fce5bb79013fb7efdd3df4624feb764f3843809d9db0abd6b7a7fe676fd880277ce7390a
Alice Secret key (only showing 1/512 of key): 7d3c1209d179008b11100d9674cb57474df22f356eaed1c28aa9da775a21b04b941654120768d8c02b0ec86480b00c97d044539677c9e67935d41c931ae77ed80a13ee4a734747b49bcfc2f9a76028d66a68ba69a2f48750ff3c7d830f8a1b545a9b9f0cc549b8601d02a8cebdb751c2525a5ddf5a928b34df01e114d74ae850a25d4ee4c5df7eb45ed23de1720961a75d01bcad44872be1d5f81e2e430ff77c1cbbc019507c0dae5702722ac4fb09681a328023d26852e0866b9808b0703de7ba89f0e6cbacff9edf9cMessage: 530f8afbc74536b9a963b4f1c4cb738bcea7403d4d606b6e074ec5d3baf39d18726003ca37a62a74d1a2f58e7506358edd4ab1284d4ae17b41e859
Signature : 530f8afbc74536b9a963b4f1c4cb738bcea7403d4d606b6e074ec5d3baf39d18726003ca37a62a74d1a2f58e7506358edd4ab1284dbae17b41e8595820cceaf000a77c7f07cd79b579451e755754b052dfdc8748e88d7225dc508cf12ee2525cabb2ec3c0cad3575953a6f479bc1834cfe3d85430480ad9bb1a29903a9The code is here [and here]:
The code compiles using the Makefile to “./rainbow-genkey”, and which is a Linux build. To run just run the executable:

Conclusion
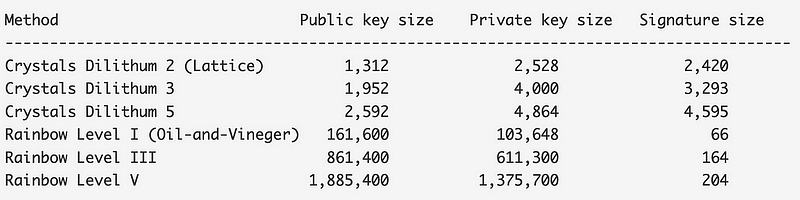
The Oil and Vinegar method is my favourite techniques in PCQ. Overall lattice methods have smaller key sizes. For Rainbow we have:
CRYPTO_PUBLICKEYBYTES = 161600
CRYPTO_SECRETKEYBYTES = 103648
CRYPTO_BYTES = 66
Signature Length = 125For Crystals Dilithum (Lattice) [here] we get:
CRYPTO_PUBLICKEYBYTES = 1312
CRYPTO_SECRETKEYBYTES = 2528
CRYPTO_BYTES = 2420
Signature Length = 2479So, Rainbow wins on the digital signature size (125 bytes) and Crystals Dilithum wins for key sizes (1,312/2,528 bytes).
Overall, Rainbow was cracked in the previous competition, but it looks like the multivariate methods are on the rise again.