ElGamal Becomes Alive in the 21st Century

ElGamal Becomes Alive in the 21st Century

And, so the RSA method came along, and it became the King of the Hill for public key encryption and digital signatures. While ECC (Elliptic Curve Cryptography) has chipped away at its dominance in digital signing, it is still the most widely used method for encryption and digital signatures. The fall of discrete logs, too, has seen the fall of DSA for signatures and the Diffie-Hellman method and being mainly replaced by elliptic curve methods (such as ECDH for most of our Web connections). But what about the ElGamal encryption method? Well, the original method used discrete logarithms, and when they fell out of favour, so did the ElGamal method. But now, with the rise of elliptic curves, the method is back and addressing many open problems in data security and trust.

If you want to understand the core method, here is a basic example using PowerShell:

https://asecuritysite.com/elgamal/elgamal_ps

Communtative Encryption

So let’s look at an example of applying the ElGamal method in the area of commutative encryption [1][here]:

With commutative encryption, we can apply Bob’s public key to a message, then encrypt with Alice’s public key. We can then decrypt with Bob’s private key, and then Alice’s private key, or decrypt with Alice’s private key and then Bob’s public key. This differs from the normal encryption process, and where we would decrypt using the reverse of the application of the keys.

Key generation

Initially, Alice generates a private key of x_1 and a public key of:

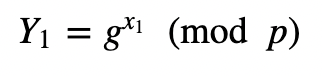
Bob generates a private key of x_2 and a public key of:

Encryption

If we have a message (M), then Alice will encrypt with:

and:

Alice will pass c_21 to Bob, and who will create:

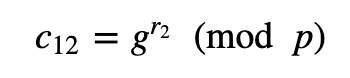
and:

The encrypted values are c11, c12 and c22.

Decryption (Bob then Alice)

To decrypt, Bob can take his key off with:

and then recover the message with:

Decryption (Alice then Bob)

To decrypt, Alice can take her key off with:

and then recover the message with:

Coding

The coding is [here]:

from Crypto.Util.number import *
from Crypto import Random
import Crypto
import random
import libnum
import sys
import hashlib
    
def primitive_root(p_val: int) -> int:
    while True:
        g = random.randrange(3, p_val)
        if pow(g, 2, p_val) == 1:
            continue
        if pow(g, p_val, p_val) == 1:
            continue
        return g
    
bits=512
M="hello"
if (len(sys.argv)>1):
    M=sys.argv[1]
if (len(sys.argv)>2):
    bits=int(sys.argv[2])
p = Crypto.Util.number.getPrime(bits, randfunc=Crypto.Random.get_random_bytes)
    
m = int.from_bytes(M.encode(),byteorder='big' ) 
        
g = primitive_root(p)  
x1 = random.randrange(3, p)  
Y1 = pow(g,x1,p)
x2 = random.randrange(3, p)  
Y2 = pow(g,x2,p)
r1=random.randrange(3, p)  
r2=random.randrange(3, p)  
print (f"Message:\nm={M}")
print (f"Bob's Public key: g={g}, Y={Y1}, p={p}\nBob's Private key: x={x1}, r1={r1}")
print (f"\nAlice's Public key: g={g}, Y={Y2}, p={p}\nAlice's Private key: x={x2}, r2={r2}")
c11=pow(g,r1,p)
c21=(pow(Y1,r1,p)*m) % p
c12=pow(g,r2,p)
c22=(pow(Y2,r2,p)*c21) % p
print (f"\nEncrypted\nc11={c11}\nc12={c12}\nc22={c22}\n")
print("First removing Alice's key then Bob's")
Alice_remove=(c22*libnum.invmod(pow(c12,x2,p),p)) % p
M_recovered=(Alice_remove*libnum.invmod(pow(c11,x1,p),p)) % p
m_rec= int.to_bytes(M_recovered,len(M),byteorder='big' ) 
print (f"\nResult: {m_rec.decode()}\n" )
print("First removing Bob's key then Alice's")
Bob_remove=(c22*libnum.invmod(pow(c11,x1,p),p)) % p
M_recovered=(Bob_remove*libnum.invmod(pow(c12,x2,p),p)) % p
m_rec= int.to_bytes(M_recovered,len(M),byteorder='big' ) 
print (f"\nResult: {m_rec.decode()}" )

A sample run for 80-bit primes [here]:

Message:
m=hello
Bob Public key: g=519160996672834189197519, Y=417750015375163083516967, p=782807293314142598778109
Bob Private key: x=10563390121140597427918, r1=239056617387655559337834
Alice Public key: g=519160996672834189197519, Y=179500691043752261889260, p=782807293314142598778109
Alice Private key: x=391602381004385515058281, r2=146527017737232627328209
Encrypted
c11=198485335807018340575441
c12=408062838808129045896002
c22=363755194689760736958184
First removing Alice key then Bob
Result: hello
First removing Bob key then Alice
Result: hello

Conclusions

If you want to learn more about the ElGamal method and its usage, try here:

https://asecuritysite.com/elgamal/

and here is an interview with the great man:

Reference

[1] Huang, K., & Tso, R. (2012, August). A commutative encryption scheme based on ElGamal encryption. In 2012 International Conference on Information Security and Intelligent Control (pp. 156–159). IEEE.