Thank Rabin and Miller for Your Online Security

Thank Rabin and Miller for Your Online Security
We live in a digitally flawed world. Very little of what we see can be truly trusted. But there are some people who have strived to make our world more trusted, and Michael O. Rabin is one of the most predominant. He was born in 1931 in Germany. In the 1960s, he worked at the University of California and MIT and then moved on to a Professorship at Harvard University. Finally, in 1981, he became a professor at the Hebrew University and has worked there ever since.
One of his classic papers [1] built on the work of Gary Miller [2]:


The paper has since provided the core method of generating prime numbers for the RSA method. Typically we generate an odd random number with a given number of bits and then test if it is a prime number. If not, we can keep adding two to the value until we reach a prime number.
Miller-Rabin test for primes
Miller-Rabin test for primes is one of the most popular methods for testing for prime numbers used in RSA. Given an odd number (n), we will have an odd number of (n−1), of which we can calculate the power of 2 with a value of s so that:
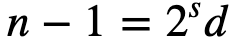
For example, if n is 25, (n−1) will be 24, and which is 2×2×2×3 and which is ²³×3. We then select a random value of a and which is between 1 and (n−1). We may have a prime if one of these is true:

and where r is a value between 0 and s−1. For example, if we take n=61, then (n−1)=60. This can be represented as: 2²×15, thus s=2 and d=15. Let’s select a=5, so we get:

This does not pass the first test, so let’s try:

and which is equal to −1 (mod 61). It may thus be a prime.
Now we will try n=719 and where (n−1)=718. (n−1)=2×359, and thus s=1 and d=359. Let’s select a=7, and so the first test is:

This has worked, so it is a possible prime. Let’s not try a=9:

and so we have more proof of it being a prime number.
In the Miller-Rabin test, we perform k trials. If any of these trails returns a false, the value is not a prime number (and is a composite. If it returns a true, it is probably prime. First, we have a number to test (n) and produce a random number (a) and then compute d to solve (and where r is a value greater than 1):

We then compute:
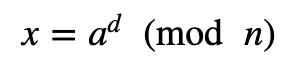
If this is 1 or -1, we return a true value for a prime number. This is coded as [here]:
while (true) {
var quotient = BigInteger.Divide(d,new BigInteger(2));
var remainder=d % 2;
if (remainder == BigInteger.One) {
break;
}
s += 1;
d = quotient;
}
var prime=false;
if (BigInteger.ModPow(a,d,n)==1) {
Console.WriteLine ("\nTest 1. It may be prime (a^d (mod n) = 1)");
prime=true;
}Next we keep squaring the value of x (mod n) while the value of d is less than (n−1) — and where we double d in each test. The code is [here]:
var a=getRandom(n);
var r=s-1;
if (BigInteger.ModPow(a,BigInteger.Pow(2,r)*d,n)==(n-1)) {
Console.WriteLine ("\nTest 2. It may be prime (a^{2^r d} (mod n) == n-1)");
prime =true;
} The code is then [here]:
namespace dotnet_rabin
{
using System.Numerics;
using System.Reflection.Metadata;
class Program {
public static BigInteger getRandom(BigInteger n){
var length=n.GetBitLength()/8+1;
Random random = new Random();
byte[] data = new byte[length];
random.NextBytes(data);
var r=new BigInteger(data)%n;
if (r.Sign==-1) r=-r;
if (r==0) r=2;
return r;
}
static void Main(string[] args)
{
var nval="997";
if (args.Length >0) nval=args[0];
var n= BigInteger.Parse(nval);
if (n == 2) {
Console.WriteLine ("2");
return;
}
if ((n % 2) == BigInteger.Zero) {
Console.WriteLine ("{0} is not prime",n);
return;
}
var s = 0;
var d = n-1;
while (true) {
var quotient = BigInteger.Divide(d,new BigInteger(2));
var remainder=d % 2;
if (remainder == BigInteger.One) {
break;
}
s += 1;
d = quotient;
}
var a=getRandom(n);
var r=s-1;
Console.WriteLine ("(n-1)=({0}-1) = 2^{1} x {2}",n,s,d);
Console.WriteLine ("s={0}, d={1}",s,d);
Console.WriteLine ("a={0}, r={1}",a,r);
var prime=false;
if (BigInteger.ModPow(a,d,n)==1) {
Console.WriteLine ("\nTest 1. It may be prime (a^d (mod n) = 1)");
prime=true;
}
if (BigInteger.ModPow(a,BigInteger.Pow(2,r)*d,n)==(n-1)) {
Console.WriteLine ("\nTest 2. It may be prime (a^{2^r d} (mod n) == n-1)");
prime =true;
}
if (prime==false) Console.WriteLine ("{0} is not a prime",n);
else Console.WriteLine ("{0} is a prime",n);
}
}
}A sample run is [here]:
(n-1)=(19-1) = 2^1 x 9
s=1, d=9
a=7, r=0
Test 1. It may be prime (a^d (mod n) = 1)
19 is a primeTrying some examples
Here are some examples to try:
- Try 19?. Try
- Try 21?. Try
- Try 27?. Try
- Try 31?. Try
- Try 33?. Try
- Try 53?. Try
- Is 7919 prime?. Try
- Is 858,599,509 prime?. Try
- Is 982,451,653 prime?. Try
- Is 982,451,652 prime?. Try
- Is 643808006…,153 prime (210 digits)?. Try
- Is 643808006…,152 prime (210 digits)?. Try
- Is 4494179990..,163 prime (210 digits)?. Try
- Is 4494179990..,162 prime (210 digits)?. Try
- Is 23097…426570593 prime (210 digits)?. Try
- Is 23097…426570595 prime (210 digits)?. Try
- Is 5521712….5385789993 prime (220 digits)?. Try
- Is 56125680…531131327771 prime (230 digits)?. Try
- Is 6413528947 … 3367 prime (125 digits)? One of the primes for RSA-250, and should be prime . Try
- Is 333720275949781565 … 062711 prime (125 digits)? One of the primes for RSA-250, and should be prime. Try
- Is 214032465024074 … 5937497937 prime (250 digits)? This is the public modulus for RSA-250, and should not be prime (as p×q). Try
Conclusions
Your online security depends on prime numbers. Any flaws in these will seriously affect the trustworthiness of your online connections, especially related to proving the identity of the systems you connect to. This typically depends on RSA signature, and which depends on random prime numbers. The Miller-Rabin test plays a core role as a method of providing a fast way to generate the required public and private keys.
References
[1] Rabin, M. O. (1980). Probabilistic algorithm for testing primality. Journal of number theory, 12(1), 128–138.
[2] Miller, G. L. (1976). Riemann’s hypothesis and tests for primality. Journal of computer and system sciences, 13(3), 300–31