Borromean Ring Signature and Privacy-Aware Transactions

Borromean Ring Signature and Privacy-Aware Transactions
In two days’ time, Bitcoin will be 15 years old. Overall, Satoshi imagined a peer-to-peer trading system which could not be stopped or compromised in any way. This new world would not involve intermediaries to determine if Bob could trade with Alice but involved miners checking every transaction. Rather than bank account details and IBAN strings, this new digital currency would use elliptic curve signing methods (ECDSA) and allow anyone to create a digital wallet without the interference of corporations. It would allow those without bank accounts to trade without any interference.
But, while it has worked well for those 15 years, it is far from perfect, and for blockchain, it can be likened to the Ford T of digital trust. For one thing, it consumes lots of energy and is slow; for another, it only uses pseudo anonymisation, and once the mapping of a wallet identifier to a person is known, users can be tracked for their purchases.
Monero
For this, the Monero cryptocurrency uses a ring-signing approach, where we can bring together a number of public keys and sign a message with just one of the private keys. This makes it difficult to find the signer of a transaction, as any of the signers could be the one who signed the transaction. Let’s say we have Alice, Bob, Carol and Dave then each will apply their public keys to the transaction, but Alice knows a secret trick and applies her private key to the signature. Overall, the transaction can be trusted, but where we cannot tell who signed it.
Monero uses a method known as RingCT and was rolled-out in Sept 2017. It is based on a paper entitled, “A Multi-layered Linkable Spontaneous Anonymous Group signature” [4]:

This method uses the Borromean Ring Signature technique at its core, and also adds a method of secretly tagging transactions, so that the anonymisation process can link them. The sender, destination and the amount transferred are all kept secret in the transaction.
Borromean Ring Signature (BRS)
With the BRS method [1], we can create a number of rings and then sign a message with one of the private keys on each of the rings. A Borromean ring, in maths, is defined as three closed curves that cannot be separated from each other but can be unknotted when one of the rings is cut or removed.
Ring signatures have been used in a range of cryptocurrency applications and are used to anonymise the sender and the recipient of a transaction. This overcomes the problem of Bitcoin, which only does pseudo-anonymity.
With an elliptic curve ring signature, we can have a private key of x, and then produce a public key of:
P=x.G
Figure 1 shows an example with four participants, and where they each have a public and private key. The public key of Participant 1 is P0 and Participant 2 has a public key of P1, and so on. Overall, we make a ring and where each participant modifies a glue value (e). This glue value starts with e0 and is used to create the signature (σ). This signature is made up from (e0 and s).
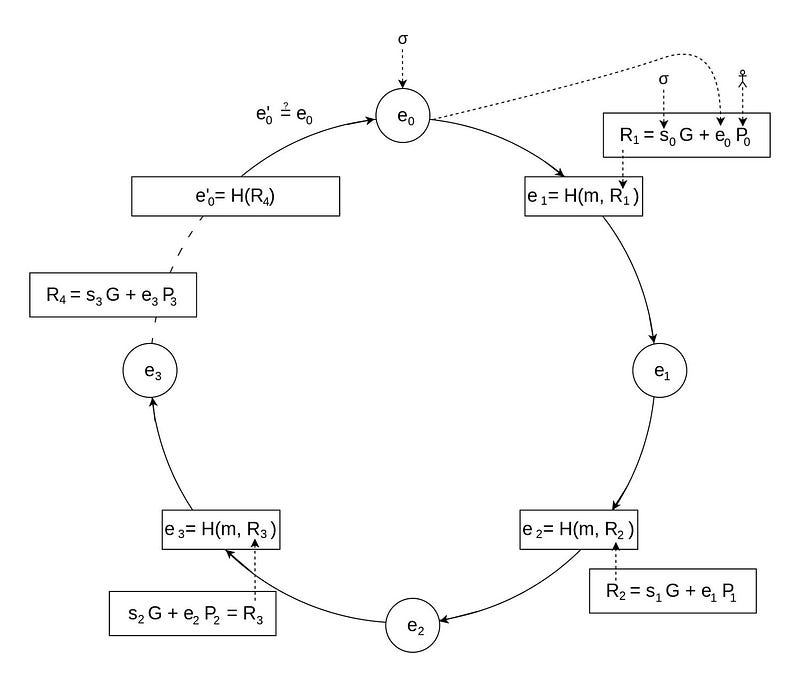
In this case, we have four signers (P0,P1,P2,P3). Initially we start with a message (M), and then append all the public keys (P0 … P3), and then hash these together:
M = H(msg || P0 || P1 || P2 || P3)
Each party (j) then modifies the glue value with:
e_{j+1}=H(m,(s_j.G+e_j_.P_j))
and where s_j is a random value generated by participant j. The trick is that the real signer — with a private key of x_j — picks a value of s_j which will close the loop. This is achieved using a chameleon hash. For this, the signer of the message (j) does not compute a random s_j, but computes:
s_j=k−x_j⋅e_j
This will allow the ring to be complete.
Coding
In this case, we have four signers (P0,P1,P2,P3), and which we can have signers of {P1 or P2 or P3} or {P1 or P2 or P3} (Code based on [3]) [here]:
package main
import (
"fmt"
"os"
"github.com/blockchain-research/crypto/brs"
)
func main() {
msg := "Hello"
argCount := len(os.Args[1:])
if argCount > 0 {
msg = os.Args[1]
}
fmt.Printf("Message to sign M=%s\n\n", msg)
//Ring [[0,1,2],[1,2,3]] means {P0 or P1 or P2} and {P1 or P2 or P3}
ring := [][]int64{[]int64{0, 1, 2}, []int64{1, 2, 3}}
//P1 makes a valid signature
signer1, verifier, err := brs.InitRing(ring, []int64{1, 1}, 4)
signature1 := signer1.Sign([]byte(msg))
result1 := verifier.Verify([]byte(msg), signature1)
if result1 {
fmt.Printf("Signature verified\n")
fmt.Printf("P1 signing\nE0=%v\n", signature1.E0)
fmt.Printf("S=%v\n\n", signature1.S)
}
//P2 makes a valid signature
signer2, verifier2, err := brs.InitRing(ring, []int64{2, 2}, 4)
if err != nil {
fmt.Printf("Fail")
}
signature2 := signer2.Sign([]byte(msg))
result2 := verifier2.Verify([]byte(msg), signature2)
if result2 {
fmt.Printf("Signature verified\n")
fmt.Printf("P2 signing\nE0=%v\n", signature2.E0)
fmt.Printf("S=%v\n\n", signature2.S)
}
//P0 and P3 makes a valid signature
signer03, verifier03, err := brs.InitRing(ring, []int64{0, 3}, 4)
if err != nil {
fmt.Printf("Fail")
}
signature03 := signer03.Sign([]byte(msg))
result3 := verifier03.Verify([]byte(msg), signature03)
if result3 {
fmt.Printf("Signature verified\n")
fmt.Printf("P0 and P3 signing\nE0=%v\n", signature1.E0)
fmt.Printf("S=%v\n\n", signature1.S)
}
}A sample run is [here]:
Signature verified
P1 signing
E0=90892453673138169846571530206319998577883367254503694839160662683125325467803
S=[[78199760025427990780505849783434141159935677659937287259452535340418036182858 74101475084685528436162390709218925627305704426403491313291896161210285302774 45451016110404674014896221332904844835928304459792201901983338362680161997056] [57372941377750809695802160090822551513043381919593035382761907489808500658574 66605268044881679287658138527446465264517871087456043429935603177450090591046 48031216691826019276590338014424313268649764849320122016317797599158435543477]]
Signature verified
P2 signing
E0=66352501961149505992530629881535018536572854263597269288507042410701026851557
S=[[14426661073808881959105837424451206667535428728250892253986120108914794211964 114146012764547141404568407797694622273129352268972250159077978577080244325250 59116972004116047353044007319901066976586694456962953703989222198762490882050] [12250041158457033295395920232837593900264786661271938343938993866188087902462 42774335825362020659383898597580920872234074472981765913524295447027276483418 11022015816325090252990938395778325758254459088234419928673246627453819502296]]
Signature verified
P0 and P3 signing
E0=90892453673138169846571530206319998577883367254503694839160662683125325467803
S=[[78199760025427990780505849783434141159935677659937287259452535340418036182858 74101475084685528436162390709218925627305704426403491313291896161210285302774 45451016110404674014896221332904844835928304459792201901983338362680161997056] [57372941377750809695802160090822551513043381919593035382761907489808500658574 66605268044881679287658138527446465264517871087456043429935603177450090591046 48031216691826019276590338014424313268649764849320122016317797599158435543477]]Conclusions
It has taken us 15 years, but we now have developed proper privacy-aware transaction methods. As I said at the start of this article, if Bitcoin is the Ford T is transaction trust, the Monero is a Tesla.
If you are interested in other range proof and bullet proof methods, try here:
https://asecuritysite.com/bulletproof/
References
[1] Maxwell, G., & Poelstra, A. (2015). Borromean ring signatures. Accessed: Jun, 8, 2019.
[3] https://github.com/blockchain-research/crypto/tree/master/brs
[4] Ren, Y., Zhao, Q., Guan, H., & Lin, Z. (2020). On design of single-layer and multilayer code-based linkable ring signatures. IEEE Access, 8, 17854–17862.