Order-Preserving Encryption (OPE)

Order-Preserving Encryption (OPE)

I keep reading papers that use Order-preserving encryption (OPE) for encrypted searches using symmetric key encryption, so I thought I would cover it in an article, such as a recent paper [here][2]:

Overall, OPE is a symmetric key encryption method that can be used to create an order on encrypted content. We will lose some information in supporting the ordering of the cyphers, but the security level should still stay acceptable for the application area. If we encrypt a value of A with a key of k to get Ek(A), and then encrypt B to get Ek(B). Then if A<B, then:

Ek(A)<Ek(B)

One of the best papers on the subject [here] is:

First, we let M and N as positive integers, and where M is less than N. We next create a random order-preserving that ranges from M to N. Then:

[M]={1,2,3,…M}

[N]={1,2,3,…N}

We can choose M random elements from [N], and arrange them in order. To encrypt a value of i, we take the i-th element of M. In real life, this would be difficult to implement, as we would need to generate many values in memory. The focus is then to create a function to generate the ith element.

To model, we can think of a large bin with a number of balls. Overall, there will be M marked balls, and M-N unmarked balls. The number of marked balls that we draw can then be defined by x, and after y samples. This is defined by a hypergeometric distribution:

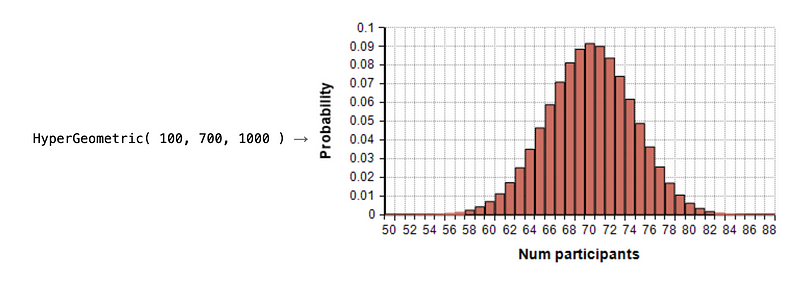
In Figure 1, we make a sample of y balls, and then plot the probability of drawing x marked balls. In this case, HyperGeometric (100, 700, 1000) defines that we sample 100 balls, and which have 700 marked balls and 300 unmarked balls. The peak probability will at 70 marked balls and 30 unmarked balls. Overall, we have a generalised form of ProbHyperGeometric(k, trials, posEvents, size), and where k is the target number of balls, trails is the number of balls that are drawn, posEvents is the number of marked balls, and the size is the total number of balls. The probability of drawing k marked balls is then::

For example, if we have 20 marked balls out of 30 balls, and draw 10 balls at a time (but do not replace them). The probability of drawing seven marked balls can then be computed with Python using:

from math import comb
a=comb(10, 3)
k=7
trails=10
posEvents=20
size=30


a=comb(posEvents,k)
b=comb(size-posEvents,trails-k)
c=comb(size,trails)
print (a*b/c)x

The result is 0.3096. We thus have around a 3-in-10 probability in drawing seven marked balls.

We can now use this to determine the number of points that lie below a given point in our range and do this by defining the range point to be the number of samples we take. and where the number of marked balls is 𝑀 and unmarked balls is 𝑁−𝑀.

More details are defined in [1]. Now, let’s implement some code [here]:

from pyope.ope import OPE, ValueRange
import sys
val1=100
val2=200
val3=300
range=1000

if (len(sys.argv)>1):
 val1=int(sys.argv[1])
if (len(sys.argv)>2):
 val2=int(sys.argv[2])
if (len(sys.argv)>3):
 val3=int(sys.argv[3])
if (len(sys.argv)>4):
 range=int(sys.argv[4])

random_key = OPE.generate_key()
cipher = OPE(random_key)

print (f"Key: {random_key.decode()}")
print (f"\nVal={val1}, Cipher={cipher.encrypt(val1)}")
print (f"Val={val2}, Cipher={cipher.encrypt(val2)}")
print (f"Val={val3}, Cipher={cipher.encrypt(val3)}")

print ("Val 1 decrypted: ",cipher.decrypt(cipher.encrypt(val1)))
print ("Val 2 decrypted: ",cipher.decrypt(cipher.encrypt(val2)))
print ("Val 3 decrypted: ",cipher.decrypt(cipher.encrypt(val3)))

cipher = OPE(b'long key' * 2, in_range=ValueRange(0, val3),out_range=ValueRange(0, range))

print(f"\nRange input range 0 to {val3}, and output range 0 to {range}")
print (f"\nVal1={val1}, Cipher={cipher.encrypt(val1)}")
print (f"Val2={val2}, Cipher={cipher.encrypt(val2)}")
print (f"Val3={val3}, Cipher={cipher.encrypt(val3)}")

A sample run shows that the values of 100, 200 add 300, are encrypted with 7,117,590, 14,119,730 and 20,705,532. With this, the encrypted values are in the same order as the input [here]:

Key: jazlAhZoQwLaruz2sEhGA9G5H7tI2RmFIxjpZn8x46g=

Val=100, Cipher=7117590
Val=200, Cipher=14119730
Val=300, Cipher=20705532
Val 1 decrypted:  100
Val 2 decrypted:  200
Val 3 decrypted:  300

We can also define an input range and an output range for the encrypted values [here]:

Range input range 0 to 300, and output range 0 to 100000

Val1=100, Cipher=33171
Val2=200, Cipher=70719
Val3=300, Cipher=99982

Conclusions

Overall, the paper [1] defines that an attacker could discover half of the bits in the plaintext when the ciphertext is analysed. So, we have to define our ranges properly.

References

[1] Boldyreva, A., Chenette, N., & O’Neill, A. (2011). Order-preserving encryption revisited: Improved security analysis and alternative solutions. In Advances in Cryptology–CRYPTO 2011: 31st Annual Cryptology Conference, Santa Barbara, CA, USA, August 14–18, 2011. Proceedings 31 (pp. 578–595). Springer Berlin Heidelberg.

[2] Rahman, Mohammad Saidur, Abdulatif Alabdulatif, and Ibrahim Khalil. “Privacy aware internet of medical things data certification framework on healthcare blockchain of 5G edge.” Computer Communications 192 (2022): 373–381.