Let’s Bet

Let’s Bet

So, let’s make a bet. There are 100 balls in a bin, and 70 of them are red and the rest are blue. You cannot see the balls in the bin, and you should not replace them once they are drawn. I want you to bet £1,000 on each draw. For this, you will draw 10 balls from the bin each time. If you draw exactly seven red balls, I will give you £4,000, but if you have any other number, I will take your money. Do you take the bet?

A good bet?

To model, we can think of a large bin with a number of balls. Overall, there will be N red balls, and M-N blue balls (and where M is initially the number of balls in the bin). The number of red balls that we draw can then be defined by x, and after y samples, and is defined by a hypergeometric distribution:

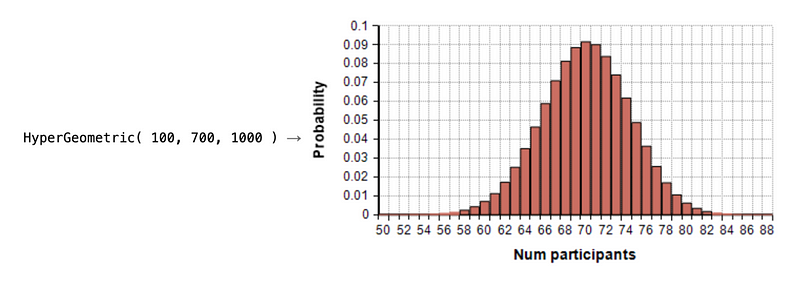
In Figure 1, we make a sample of y balls, and then plot the probability of drawing x red balls. In this case, HyperGeometric (100, 700, 1000) defines that we sample 100 balls, and which has 700 red balls and 300 blue balls. The peak probability will at 70 red balls and 30 blue balls.

Overall, we have a generalised form of ProbHyperGeometric(k, trials, posEvents, size), and where k is the target number of balls, trails is the number of balls that are drawn, posEvents is the number of marked balls, and the size is the total number of balls. The probability of drawing k marked balls is then:

For example, if we have 20 marked balls out of 30 balls, and draw 10 balls at a time (but do not replace them). The probability of drawing seven red balls from 10 can then be computed with Python using:

from math import comb

k=7
trails=10
posEvents=70
size=100

a=comb(posEvents,k)
b=comb(size-posEvents,trails-k)
c=comb(size,trails)
print (a*b/c)

The result is 0.3096. We thus have around a 3-in-10 probability in drawing seven marked balls. This will mean that if we have three goes, we are likely to win won of them. Our stake for three games will be £3,000, and we are, on average, likely to win £4,000.

So, it’s a good bet!

Go fall in love with maths.

To see where this is used in cybersecurity, try here: