Cracking Crypto with Lattices

Cracking Crypto with Lattices
Cryptography is the fundamental building block for cybersecurity, and any weaknesses may compromise digital trust. One method that can be used to test the security of our developed methods is the LLL algorithm — named after Arjen Lenstra, Hendrik Lenstra Jr. and László Lovász. While useful, it still can struggle in terms of performance, but a new paper outlines a new way to significantly boost performance [here]:

In fact, the paper recently won the Best Paper award at the 2023 Crypt conference [here], and now opens up many new areas of application for the LLL method.
Lattices
With lattice cryptography, we create a lattice of points, and then introduce a small error in the point, and it then becomes a hard problem to find the nearest point to the point with the error.
Lattice cryptography is seen as a replacement for our existing public key methods. What is so good about them is that we have a provably hard problem. So, I’m going to show that this is a hard problem and is based on this YouTube video [here]. In the presentation, we look at the CVP (Closest Vector Problem), and where we have it, we find the closest point. For simplicity, we take two vectors (v1 and v2), and which connect from the origin to two points. We then find a solution for:

If v1 and v2 are orthogonal (they are almost at right angles to each other), Baini’s algorithm allows us to find the closest points, if not, we will get an incorrect answer. In order to test if we have a nearly orthogonal match between two points, we calculate:
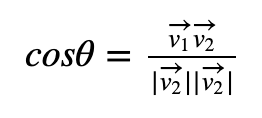
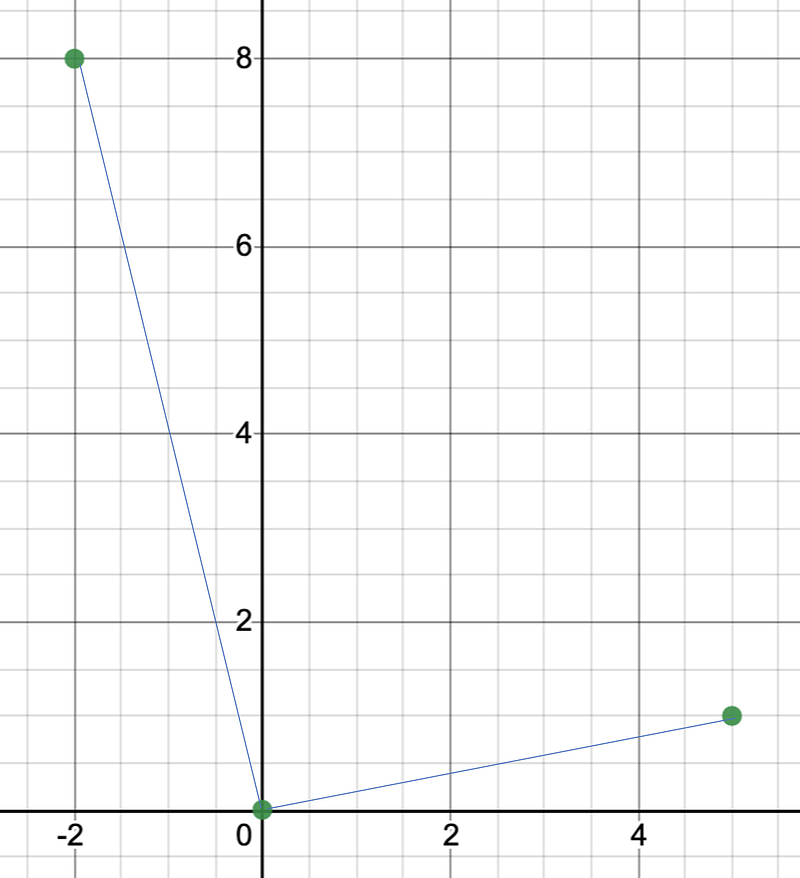
We thus want cosθ to be close to zero. If we define one vector (v1→) with (5,1) and another vector (v2→) with (-2,8), we get the following lattice [here]:

Now we want to find the nearest point to (27,8). First, we determine if the angle between the points is around 90 degrees and, if it is, we should be able to solve for the nearest point using Babai’s algorithm:
We can now solve:
a(5)+b(1)=27
a(−2)+b(8)=8
For this, we can solve the linear equation for a and b to get a=5.52 and b=0.309. This is then rounded to a=6 and b=0, to give a vector point of (30,6), and which is close to (27,8):
Cos theta: -0.04756514941544941
Grid point: 5 1
Grid point: -2 8
Solution (not rounded): 5.523809523809524 0.3095238095238095
Solution: 6.0 0.0
Nearest: 30.0 6.0The Python code for this is [here]:
import numpy as np
import numpy as np
import math
x1=5
y1=1
x2=-2
y2=8
x=27
y=8
costheta = ((x1*x2)+(y1*y2))/(math.sqrt(x1*x1+y1*y1)*math.sqrt(x2*x2+y2*y2))
print ("Cos theta: ",costheta)
print ("Grid point: ",x1,y1)print ("Grid point: ",x2,y2)
_solve1 = np.array([[x1,x2], [y1,y2]])
_solve2 = np.array([x,y])
x = np.linalg.solve(_solve1, _solve2)
a=round(x[0],0)
b=round(x[1],0)
print ("Solution (not rounded): ",x[0],x[1])
print ("Solution: ",a,b)
print ("Nearest: ",x1*a+x2*b,y1*a+y2*b)
solx=x1*a+x2*bsoly=y1*a+y2*bNow if we try two other vectors in the lattice of (37,41) and (103,113), the angle between them (Cos(theta)) is nearly zero, so we should not be able to solve:
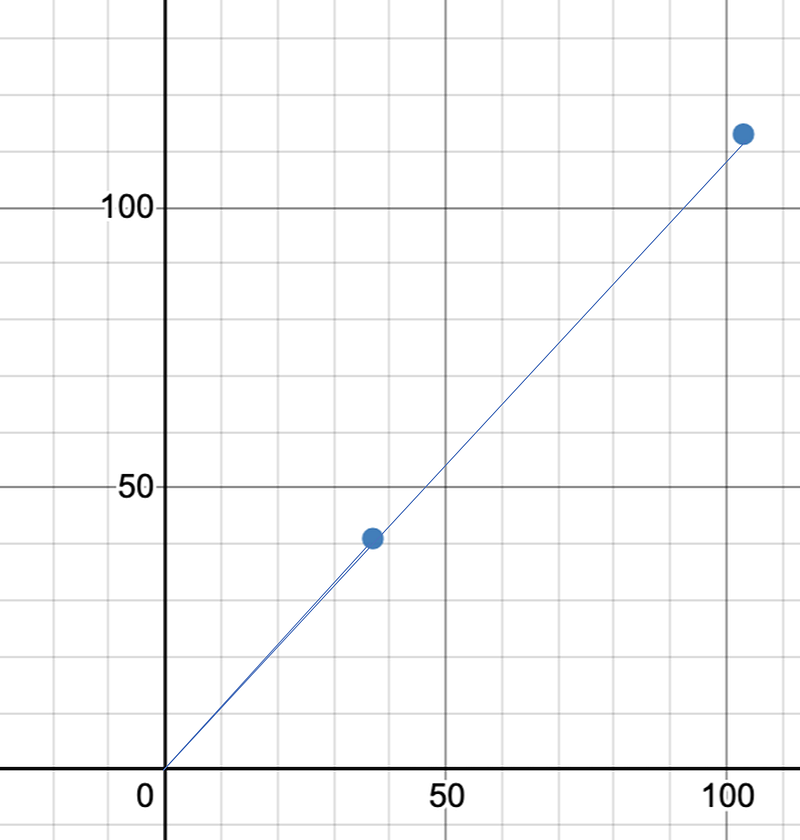
In this case, we get a solution of (-53,10) which gives us an incorrect point of (-4,-26) and which is not near (27,8):
Grid point: 37 41
Grid point: 103 113
Costheta: 0.9999876301601318
Solution (not rounded): -53.0 19.0
Solution: -53.0 19.0
Nearest: -4.0 -26.0We thus get the wrong answer, and this is what makes lattice crypto a hard problem. If we now try and solve for the point we found in the first part (30,6), we then get a correct solution for (37,41) and (103,113):
Grid point: 37 41
Grid point: 103 113
Solution (not rounded): -66.0 24.0
Solution: -66.0 24.0
Nearest: 30.0 6.0So, we basically need to have orthogonal points on the lattice, and the solution becomes simple [here].
The new LLL method
As we have seen in Figure 1, every lattice can be defined by its basis, and which is a set of vectors that describe every point on the lattice. But, there is not just a single set of vectors that describe the lattice, and not all the vectors have the same features. If we use vectors which are short and at right angles to each other, they can be efficient for solving a range of problems — including factorization problems. The finding of these vectors is known as lattice basis reduction.
The major problem with current LLL methods is that they struggle with a large number of inputs. Ryan and Heninger’s paper defines a new way of breaking the task to be solved into smaller elements, along with reducing number precision. This compresses the numerical values and supports the reduction of a lattice which has thousands of dimensions
Lenstra–Lenstra–Lovász (LLL)
The Lenstra–Lenstra–Lovász (LLL) method [paper][2]. This outlined a method that could be used to crack a digital signature and discover the private key used to digitally sign the message. This can search for the private key that has been used to sign a message with ECDSA.
One of the most common signatures is ECDSA (Elliptic Curve Digital Signature Algorithm) and which is used with Bitcoin and Ethereum. With this, Bob creates a random private key (priv), and then a public key from:

Next, in order to create a signature for a message of M, he creates a random number (k) and generates the signature of:

The signature is then (r,s) and where r is the x-co-ordinate of the point kG. H(M) is the SHA-256 hash of the message (M), and converted into an integer value. If the k value is revealed for any of the signatures, an intruder can determine the private key using:
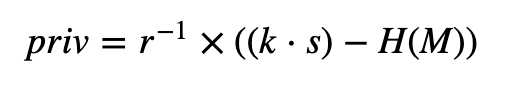
This works because:

and so:

and for priv:

We can then use the code [here] to implement a searching method based on LLL [here]:
import ecdsa
import random
import libnum
import olll
import hashlib
import sys# https://blog.trailofbits.com/2020/06/11/ecdsa-handle-with-care/
G = ecdsa.NIST256p.generator
order = G.order()print ("Curve detail")
print (G.curve())
print ("Order:",order)
print ("Gx:",G.x())
print ("Gy:",G.y())
priv = random.randrange(1,order)
Public_key = ecdsa.ecdsa.Public_key(G, G * priv)
Private_key = ecdsa.ecdsa.Private_key(Public_key, priv)
k1 = random.randrange(1, pow(2,127))
k2 = random.randrange(1, pow(2,127))msg1="Hello"
msg2="Hello1"if (len(sys.argv)>1):
msg1=(sys.argv[1])
if (len(sys.argv)>2):
msg2=(sys.argv[2])m1 = int(hashlib.sha256(msg1.encode()).hexdigest(),base=16)
m2 = int(hashlib.sha256(msg2.encode()).hexdigest(),base=16)
sig1 = Private_key.sign(m1, k1)
sig2 = Private_key.sign(m2, k2)print ("\nMessage 1: ",msg1)
print ("Message 2: ",msg2)
print ("\nSig 1 r,s: ",sig1.r,sig1.s)
print ("Sig 2 r,s: ",sig2.r,sig2.s)
print ("\nk1: ",k1)
print ("k2: ",k2)print ("Private key: ",priv)r1 = sig1.r
s1_inv = libnum.invmod(sig1.s, order)
r2 = sig2.r
s2_inv = libnum.invmod(sig2.s, order)
matrix = [[order, 0, 0, 0], [0, order, 0, 0],
[r1*s1_inv, r2*s2_inv, (2**128) / order, 0],
[m1*s1_inv, m2*s2_inv, 0, 2**128]]
search_matrix = olll.reduction(matrix, 0.75)
r1_inv = libnum.invmod(sig1.r, order)
s1 = sig1.s
for search_row in search_matrix:
possible_k1 = search_row[0]
try_private_key = (r1_inv * ((possible_k1 * s1) - m1)) % order
if ecdsa.ecdsa.Public_key(G, G * try_private_key) == Public_key:
print("\nThe private key has been found")
print (try_private_key)A sample run is [here]:
Curve detail
CurveFp(p=115792089210356248762697446949407573530086143415290314195533631308867097853951, a=-3, b=41058363725152142129326129780047268409114441015993725554835256314039467401291, h=1)
Order: 115792089210356248762697446949407573529996955224135760342422259061068512044369
Gx: 48439561293906451759052585252797914202762949526041747995844080717082404635286
Gy: 36134250956749795798585127919587881956611106672985015071877198253568414405109Message 1: hello
Message 2: goodbyeSig 1 r,s: 115147473306387600780958700123813228515236063210926878166205132442387398405974 78422551211706787416844282162734821752165856246967039833155909830188362436931
Sig 2 r,s: 72928835934664146344187979593177679887058837944881110039604237325952057142506 34831214671095490475430891005520988929988430486970993941519827388518136205821k1: 2238116107289725910464212774221939217
k2: 23155266189808659522258191324208917771
Private key: 3126769432554995310932591745910468237140199425344791317304188208833915624553It is a truly fantastic paper, and well worth a read.
In December 2019, a team led by Paul Zimmermann of INRIA announced the factorization of the largest-ever RSA modulus (RSA-240):
RSA-240 = 124620366781718784065835044608106590434820374651678805754818788883289666801188210855036039570272508747509864768438458621054865537970253930571891217684318286362846948405301614416430468066875699415246993185704183030512549594371372159029236099RSA-240 = 509435952285839914555051023580843714132648382024111473186660296521821206469746700620316443478873837606252372049619334517
× 244624208838318150567813139024002896653802092578931401452041221336558477095178155258218897735030590669041302045908071447The factorization involved factorizing a 795-bit integer into its prime number factors. It caused industry experts to define that RSA would only be safe with at least 2,048-bit keys. Actually, it was Arjen, in the 1990s, who was the first to crack the early RSA challenges, and managed to factorize 330 (100 decimal digits), 364, 426 and 430-bit modulus values [here]:

Conclusions
The new method is perhaps just the start of a whole new analysis of our existing public key encryption methods. They are already crumbling due to the advent of quantum computers, but this paper may accelerate their demise.
References
[1] Lenstra, A. K., Lenstra, H. W., & Lovász, L. (1982). Factoring polynomials with rational coefficients. Mathematische annalen, 261(ARTICLE), 515–534.