Analysis of pulses

[Back] The signal shape of most interest in data communications is the repetitive rectangular pulse. With a pulse we see a sin(x)/x response:

Options

Frequency (Hz)

Try an example

Duty = 0.3 Calc
Duty = 0.5 Calc
Duty = 0.8 Calc
Duty = 0.8, Freq=3Hz Calc
Duty = 0.2, Freq=2Hz Calc
Duty = 0.1, Freq=1Hz Calc
Duty = 0.5, Freq=1Hz Calc

The blue broken line is the expected response given a sine cardinal (sinc) which is a sin(x)/x function.

The green broken line represents the reconstructed waveform based on the first eight harmonics (note that the reconstructed pulses have been shifted by t/2 - which is half of the pulse width).

Freq = 0 Hz 1.0 Freq = 2.0 Hz 1.8722101893680592 Freq = 4.0 Hz 1.5176445851565756 Freq = 6.0 Hz 1.015102832849491 Freq = 8.0 Hz 0.47270539143623036 Freq = 10.0 Hz 4.1215620227014583e-17 Freq = 12.0 Hz 0.3193404232376472 Freq = 14.0 Hz 0.4467368588074236 Freq = 16.0 Hz 0.3948310381102986

[View]

Theory

The signal shape of most interest in data communications is the repetitive rectangular pulse, as shown in Figure 1. It is defined by its amplitude and its duty cycle, which is the ratio of the active time of the pulse (t) to the period of the waveform (T). The duty cycle is thus given by:

Duty Cycle =\(\frac{t}{T}\)

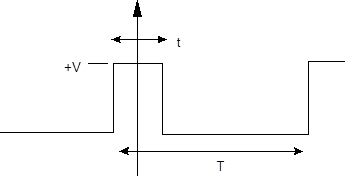
Figure 1:Pulse

The time-based repetitive pulse waveform is given by:

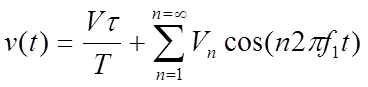
the amplitudes of the harmonics is given by:

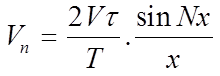
where:

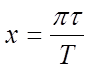
This has the response of a sin(x)/x function:

Source code

The following outlines the Python code used:

import matplotlib.pyplot as plot
import numpy as np
import sys
from scipy import signal

file ='1111'
freq=2.0
duty=0.2

if (len(sys.argv)>1):
        file=str(sys.argv[1])

if (len(sys.argv)>2):
        duty=float(sys.argv[2])

if (len(sys.argv)>3):
        freq=float(sys.argv[3])

Fs = 100.0;  # sampling rate
Ts = 1.0/Fs; # sampling interval

t = np.arange(0,2,Ts)


y = 2.5*signal.square(2 * np.pi * freq * t, duty=duty)+2.5

 
n = len(y) # length of the signal
k = np.arange(n)
T = n/Fs
frq = k/T # two sides frequency range
frq = frq[range(n/2)] # one side frequency range
Y = np.fft.fft(y)/n # fft computing and normalization
Y = 2*Y[range(n/2)]

fig,myplot = plot.subplots(2, 1)
myplot[0].plot(t,y) 
myplot[0].set_xlabel('Time')
myplot[0].set_ylabel('Amplitude')

myplot[1].plot(frq,abs(Y),'r') # plotting the spectrum

frq =np.delete(frq,0,0)

y1=2*5*duty*np.sin(np.pi*duty*frq/freq)/(np.pi*duty*frq/freq) 

y1=np.insert(y1,0,5*duty)
frq=np.insert(frq,0,0)

myplot[1].plot(frq,abs(y1),'--b') 
myplot[1].set_xlabel('Freq (Hz)')
myplot[1].set_ylabel('|Y(freq)|')

#print frq
print 'Freq = 0 Hz\t',str((y1)[0])
print 'Freq =',frq[2*freq],'Hz\t',str(abs(Y[2*freq]))
print 'Freq =',frq[4*freq],'Hz\t',str(abs(Y[4*freq]))
print 'Freq =',frq[6*freq],'Hz\t',str(abs(Y[6*freq]))
print 'Freq =',frq[8*freq],'Hz\t',str(abs(Y[8*freq]))
print 'Freq =',frq[10*freq],'Hz\t',str(abs(Y[10*freq]))
print 'Freq =',frq[12*freq],'Hz\t',str(abs(Y[12*freq]))
print 'Freq =',frq[14*freq],'Hz\t',str(abs(Y[14*freq]))
print 'Freq =',frq[16*freq],'Hz\t',str(abs(Y[16*freq]))

h1=y1[0]
h2=y1[2*freq]
h3=y1[4*freq]
h4=y1[6*freq]
h5=y1[8*freq]
h6=y1[10*freq]
h7=y1[12*freq]

yupdate = h1+h2*np.cos(2 * np.pi * freq * t)+h3*np.cos(2*2 * np.pi * freq * t) \
+h4*np.cos(3*2 * np.pi * freq * t)+h5*np.cos(4*2 * np.pi * freq * t) \
+h6*np.cos(5*2 * np.pi * freq * t)+h7*np.cos(6*2 * np.pi * freq * t)

myplot[0].plot(t,abs(yupdate),'--g') 

f1 = file+".svg"
plot.savefig(f1)

f2= file+".png"
plot.savefig(f2,format='PNG')

plot.show()