Elliptic curves are used fairly extensively in public key encryption (such as in Bitcoin and Tor). A BN-curve (Barreto-Naehrig curve) [paper] defines an elliptic curve which can be used for pairings that allow for a high security and efficiency level.
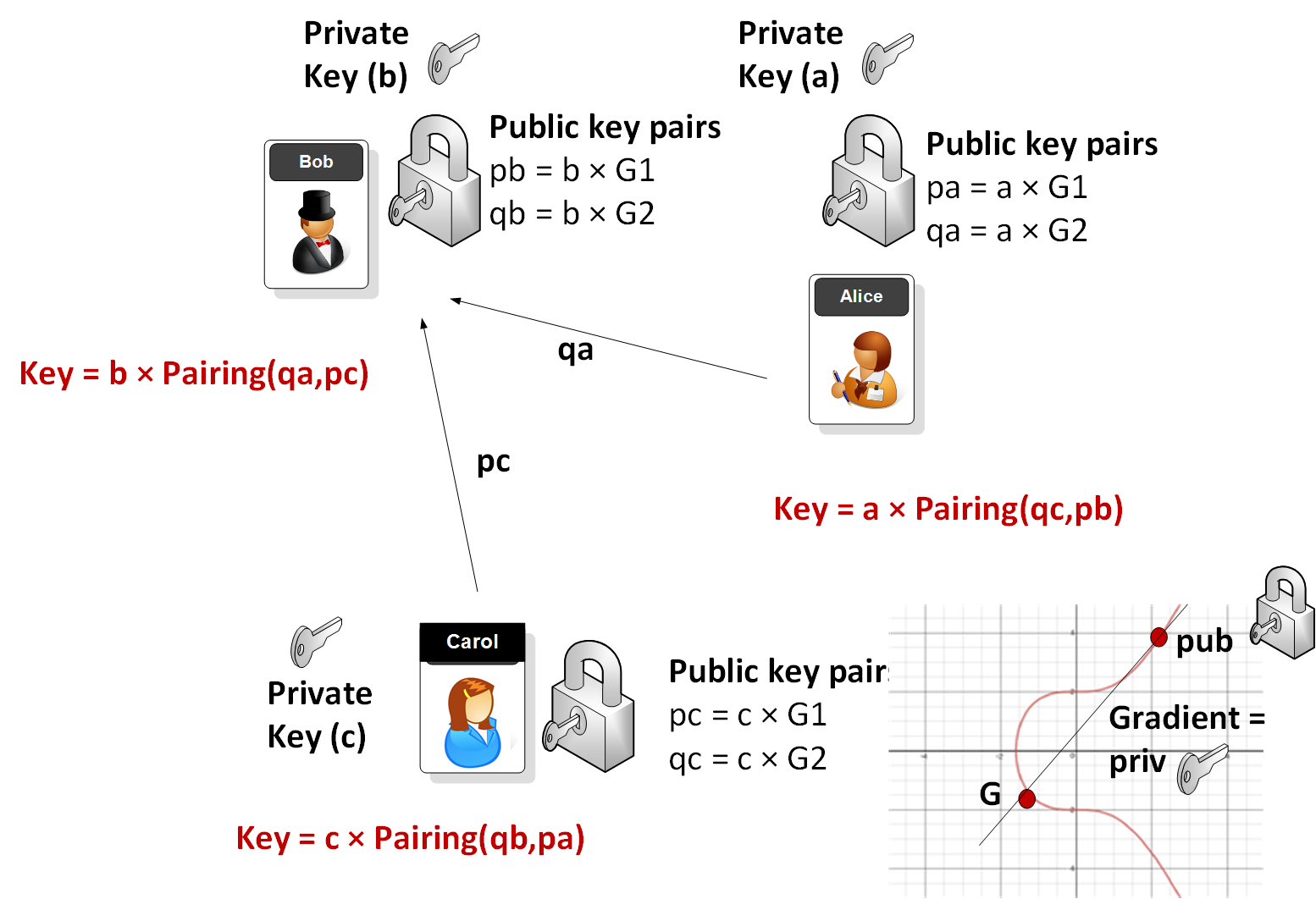
So how do we generate a shared key between three parties? This page implements the tripartite Diffie-Hellman algorithm [Paper] and what Bob (B), Alice (A) and Carol (C) share their key pairings and then can calculate a shared secret key. In this case a, b and c are the private keys generated by Alice, Bob and Carol, respectively. Bob, Alice and Carol then generate key public keys from curves G1 and G2. In this case we show the keys for Alice, which are pa (\(pa = a \times G1\)), and qa (\(qa = a \times G2\)). Alice then calculate the shared key by taking the public values passed from Bob and Alice, and then multiplying it by her secret key (a):