In the Bleichenbacher's attack the intruder captures the cipher for the pre-shared key, and then re-ciphers with the additional of a value s:
Bleichenbacher's attack |
Outline
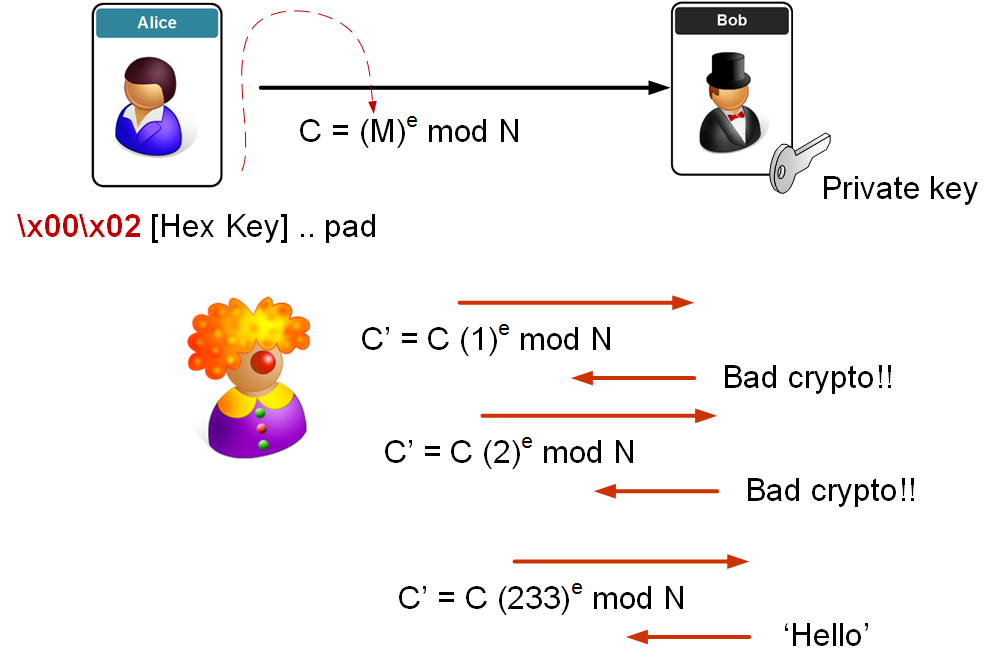
This is Bleichenbacher's attack [here] and has been the core of many attacks on SSL.
Let's say that Eve is attacking the server. In the message she sends, there's padding of the pre-shared key (as it is much smaller than the public modulus - n). In PKCS#1 v1.5 padding we then have two bytes at the start:
0x00 0x02
Eve then captures the cipher in the handshake and which contains the SSL pre-shared key (M):
\(C = M^e \mod N\)
She then plays it back to the server, but adds an 's' value (where she multiplies the cipher (C) by s to the power of e (mod N)):
\(C' = C \times (s^e) \mod N\)
where e and N are the known public key elements. The server decrypts and gets:
\(M' = (C(s^e))^d \mod N = C^d \times s^{ed} \mod N = M \times s \mod N\)
\(M = \frac{C'}{s}\)
When the server reads this, the first two bytes are likely to be incorrect, so it responds to say "Bad Crypto!". Eve then keeps trying with different s values, until the server gives her a positive response, and she's then on her way to finding the key. As we have 16 bits at the start, it will take us between 30,000 (1 in \(2^{15}\) which is 1-in-32,728) and 130,000 attempts (1 in \(2^{17}\) which is 1-in-131,073) to get a successful access.
We use padding to make sure that M (the pre-shared key) is the same length as the modulus (n). As M is only 48 bytes, we need to pad to give a length equal to n (256 bytes for a 2048-bit key).
In the end we just need to divide the original cipher by the value we have found, and we get M.
Coding
In this case we capture the cipher with M (which starts with \x00\x02), and then play it back with the addition of s^e, and then detect when there is a success in the cipher code:
import sys
e=79
d=1019
N=3337
def int_to_bytes(val, num_bytes):
return [(val & (0xff << pos*8)) >> pos*8 for pos in range(num_bytes)]
print ('==Initial values ====')
print ('e=',e,'d=',d,'N=',N)
print ('\n=============')
pad = ('\x00\x02\x55\x55')
val = int.from_bytes(pad.encode(), byteorder='big', signed=False)
print ('Padding is:',pad,' Int:',val)
cipher = val**e % N
print ('Cipher is: ',cipher)
for s in range(0,255):
cipher_dash = (cipher*(s**e)) % N
decode = cipher_dash **d % N
result = int_to_bytes(decode,2)
print (s,end='')
if (result[0]==0 and result[1]==2):
print ('\n\\x00\\x02 Found it at s=',s)
break
Key calculation
Let’s select:
P=47 Q=71
The calculation of n and PHI is:
n=P × Q = 13 × 11 = 3337 PHI = (p-1)(q-1) = 3220
We can select e as:
e = 79
Next we can calculate d from:
(79 × d) mod 3220 = 1 [Link] d = 1019 Encryption key [3337,79] Decryption key [3337,1019]
Then, with a message of 688, we get:
\(Cipher = (688)^{79} \mod 3337 = 1570\)
\(Decoded = (1570)^{1019} \mod 3337 = 688\)