Differential Cryptanalysis (AES ECB)A differential attack on a block cipher is where we analyse the change between one plaintext value and another, and the change that it makes on the output ciphers. In many cases we change one bit in the input, and observe one bit change on the input and observe the change in the output. A well designed cipher will cause an average of 50% of the bits to change. If the result is non-random, it gives an attacker an advantage in cracking the block cipher. In the following we change one bit of the plain text and then analyse the ciphertext for the number of bits that change [AES ECB][Hash][AES CBC][AES CFB][AES CTR]: |
Outline
A differential attack on a block cipher is where we analyse the change between one plaintext value and another, and the change that it makes on the output ciphers. In many cases we change one bit in the input, and observe one bit change on the input and observe the change in the output. A well designed cipher will cause an average of 50% of the bits to change. If the result is non-random, it gives an attacker an advantage in cracking the block cipher.
The differential cryptanalysis method was created in the 1990s and where it was possible to change a single bit in plaintext (P and P’) and then observe the change in the output ciphertext (C and C’):
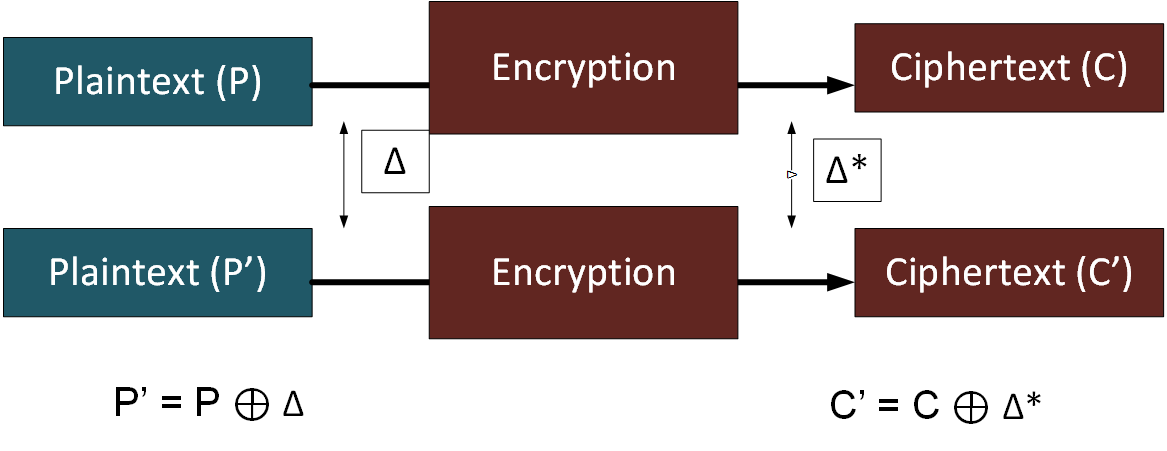
The difference in encryption is then created with the addition of the key, and where parts of the key will be revealed through the differential method.
An S-box is often used in a crypto method, and where it is possible to follow a bit through each round and watch how it will be routed to the output, and we can then discover parts of the keys. As the differential cryptanalysis was being defined, IBM found-out that a common encryption method — DES (Data Encryption Standard) — was free of attacks for its S-boxes. It has since been shown that the NSA had actually defined an update to the original S-box specification for DES, in order to improve its resistance. It is thought that the NSA was actually trying to shore-up the DES method, in order that differential cryptanalysis would not show that it to be flawed.
While the differential cryptanalysis was published by Eli Biham and Adi Shamir in the late 1980s, it is thought that the NSA already knew about the technique before it was made public.
A sample run for a message of "abct" and a key of "qwerty" gives 70 bit changes out of 128:
Message abct Key qwerty Cipher (ECB) [0 bit change]: 2fd0f45442bd725b070311d4fec4e400 Cipher (ECB) [1 bit change]: 9f44e309f1f77d1dc6feb9417ff5ff28 Bits changed: 70 out of 128 ( 54 %) Cipher1: 00101111110100001111010001010100010000101011110101 Cipher2: 10011111010001001110001100001001111100011111011101 Changes: X-XX----X--X-X-----X-XXX-X-XXX-XX-XX--XX-X--X-X---
The sample code is:
from Crypto.Cipher import AES
import hashlib
import sys
import binascii
import Padding
from bitstring import BitArray
val='hello'
password='qwerty'
plaintext=val
def tobits(s):
instr=binascii.hexlify(s).decode()
c = BitArray(hex=instr)
return c.bin
def frombits(bits):
chars = []
for b in range(len(bits) // 8):
byte = bits[b*8:(b+1)*8]
chars.append(chr(int(''.join([str(bit) for bit in byte]), 2)))
return ''.join(chars)
def encrypt(plaintext,key, mode):
encobj = AES.new(key,mode)
return(encobj.encrypt(plaintext))
def decrypt(ciphertext,key, mode):
encobj = AES.new(key,mode)
return(encobj.decrypt(ciphertext))
def diff(c1,c2):
counter=0
str1=''
str2=''
str3=''
for x in range(len(c1)):
str1 = str1+str(c1[x])
str2 = str2+str(c2[x])
if (c1[x]==c2[x]):
counter=counter+1
str3=str3+"-"
else:
str3=str3+"X"
return str1,str2,str3,counter
key = hashlib.sha256(password.encode()).digest()
print("Message:\t",plaintext)
print("Key:\t\t",password)
plaintext= Padding.appendPadding(plaintext,blocksize=Padding.AES_blocksize,mode='CMS')
plaintext2 = bytearray(plaintext.encode())
plaintext2[0]=plaintext2[0] ^ 1
plaintext2 = bytes(plaintext2).decode()
print ("\nPlain (original plain):\t",plaintext.encode())
print ("Plain (1 bit change):\t",plaintext2.encode())
ciphertext1 = encrypt(plaintext.encode(),key,AES.MODE_ECB)
ciphertext2 = encrypt(plaintext2.encode(),key,AES.MODE_ECB)
cipherbits1= tobits(ciphertext1)
print("\nCipher (ECB) [0 bit change]: ",binascii.hexlify(bytearray(ciphertext1)))
cipherbits2 = tobits(ciphertext2)
print("Cipher (ECB) [1 bit change]: ",binascii.hexlify(bytearray(ciphertext2)))
str1,str2,str3,counter = diff(cipherbits1,cipherbits2)
print("\nBits changed:",counter," out of ",len(cipherbits1))
print("Cipher1:",str1[:50])
print("Cipher2:",str2[:50])
print("Changes:",str3[:50])
res1= decrypt(ciphertext1,key,AES.MODE_ECB)
res2= decrypt(ciphertext2,key,AES.MODE_ECB)
print ("\n\nDecrypt Res 1:\t",Padding.removePadding(res1.decode(),blocksize=Padding.AES_blocksize,mode='CMS'))
print ("Decrypt Res 1:\t",Padding.removePadding(res2.decode(),blocksize=Padding.AES_blocksize,mode='CMS'))