Differential Cryptanalysis (Hash)A differential attack on a block cipher is where we analyse the change between one plaintext value and another, and the change that it makes on the output ciphers. In many cases we change one bit in the input, and observe one bit change on the input and observe the change in the output. A well designed cipher will cause an average of 50% of the bits to change. If the result is non-random, it gives an attacker an advantage in cracking the block cipher. In the following we change one bit of the plain text and then analyse the ciphertext for the number of bits that change. In this case we will change one bit of a plaintext string, and see how many bits will change in the generated hash value [related article][AES ECB][Hash][AES CBC][AES CFB][AES CTR]: |
Outline
A differential attack on a block cipher is where we analyse the change between one plaintext value and another, and the change that it makes on the output ciphers. In many cases we change one bit in the input, and observe one bit change on the input and observe the change in the output. A well designed cipher will cause an average of 50% of the bits to change. If the result is non-random, it gives an attacker an advantage in cracking the block cipher.
The differential cryptanalysis method was created in the 1990s and where it was possible to change a single bit in plaintext (P and P’) and then observe the change in the output ciphertext (C and C’):
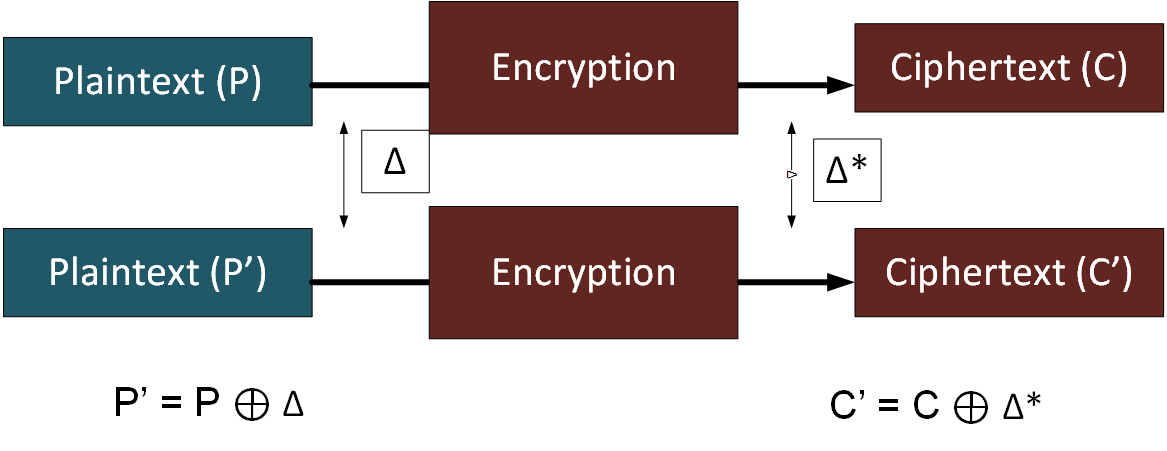
The difference in encryption is then created with the addition of the key, and where parts of the key will be revealed through the differential method.
An S-box is often used in a crypto method, and where it is possible to follow a bit through each round and watch how it will be routed to the output, and we can then discover parts of the keys. As the differential cryptanalysis was being defined, IBM found-out that a common encryption method — DES (Data Encryption Standard) — was free of attacks for its S-boxes. It has since been shown that the NSA had actually defined an update to the original S-box specification for DES, in order to improve its resistance. It is thought that the NSA was actually trying to shore-up the DES method, in order that differential cryptanalysis would not show that it to be flawed.
While the differential cryptanalysis was published by Eli Biham and Adi Shamir in the late 1980s, it is thought that the NSA already knew about the technique before it was made public.
In this case we will try different hashing methods, and determine the number of bits that will change. A sample run for a message of "abc" gives 58 bit changes out of 128:
Plaintext 1: abc Plaintext 2: ábc Hash 1: 900150983cd24fb0d6963f7d28e17f72 Hash 2: 73daa9468b3e3999589875343afa18f5 Bits changed: 58 out of 128 ( 45 %) Cipher1: 10010000000000010101000010011000001111001101001001 Cipher2: 01110011110110101010100101000110100010110011111000 Changes: XXX---XXXX-XX-XXXXXXX--XXX-XXXX-X-XX-XXXXXX-XX---X
If we now try with SHA-512 we get a 50% change:
Plaintext 1: abc Plaintext 2: ábc Hash 1: ddaf35a193617abacc417349ae20413112e6fa4e89a97ea20a9eeee64b55d39a2192992a274fc1a836ba3c23a3feebbd454d4423643ce80e2a9ac94fa54ca49f Hash 2: 6f2b2f91ea5b6457a886ea2533afbaa775a007cb3f8ede145a5f64dc8958218fd5fedf32da21974166500870b9faea1c13e16602166a36c768d007345bbede3c Bits changed: 261 out of 512 ( 50 %) Cipher1: 11011101101011110011010110100001100100110110000101 Cipher2: 01101111001010110010111110010001111010100101101101 Changes: X-XX--X-X----X-----XX-X---XX-----XXXX--X--XXX-X---
The sample code is:
import hashlib
import sys
import binascii
import Padding
from functools import reduce
plaintext1='hello'
def toHex(s):
lst = []
for ch in s:
hv = hex(ord(ch)).replace('0x', '')
if len(hv) == 1:
hv = '0'+hv
lst.append(hv)
return reduce(lambda x,y:x+y, lst)
def tobits(s1):
s= bytearray.fromhex(s1)
result = []
for c in s:
bits = bin(c)[2:]
bits = '00000000'[len(bits):] + bits
result.extend([int(b) for b in bits])
return result
def frombits(bits):
chars = []
for b in range(len(bits) // 8):
byte = bits[b*8:(b+1)*8]
chars.append(chr(int(''.join([str(bit) for bit in byte]), 2)))
return ''.join(chars)
def diff(c1,c2):
counter=0
str1=''
str2=''
str3=''
for x in range(len(c1)):
str1 = str1+str(c1[x])
str2 = str2+str(c2[x])
if (c1[x]==c2[x]):
counter=counter+1
str3=str3+"-"
else:
str3=str3+"X"
return str1,str2,str3,counter
if (len(sys.argv)>1):
plaintext1=str(sys.argv[1])
if (len(sys.argv)>2):
type=int(sys.argv[2])
if (type==1):
ciphertext1 = hashlib.md5(plaintext1.encode()).hexdigest()
elif (type==2):
ciphertext1 = hashlib.sha1(plaintext1.encode()).hexdigest()
elif (type==3):
ciphertext1 = hashlib.sha224(plaintext1.encode()).hexdigest()
elif (type==4):
ciphertext1 = hashlib.sha256(plaintext1.encode()).hexdigest()
else:
ciphertext1 = hashlib.sha512(plaintext1.encode()).hexdigest()
cipherbits1 = tobits(ciphertext1)
bits = tobits(toHex(plaintext1))
bits[0]=bits[0]^1
plaintext2 = frombits(bits)
if (type==1):
ciphertext2 = hashlib.md5(plaintext2.encode()).hexdigest()
elif (type==2):
ciphertext2 = hashlib.sha1(plaintext2.encode()).hexdigest()
elif (type==3):
ciphertext2 = hashlib.sha224(plaintext2.encode()).hexdigest()
elif (type==4):
ciphertext2 = hashlib.sha256(plaintext2.encode()).hexdigest()
else:
ciphertext2 = hashlib.sha512(plaintext2.encode()).hexdigest()
cipherbits2 = tobits(ciphertext2)
str1,str2,str3,counter = diff(cipherbits1,cipherbits2)
ratio = 100*counter/len(cipherbits1)
print("\nPlaintext 1:",plaintext1)
print("Plaintext 2:",plaintext2)
print("\nHash 1:",ciphertext1)
print("Hash 2:",ciphertext2)
print("\nBits changed:",counter," out of ",len(cipherbits1), "(",ratio,"%)")
print("Cipher1:",str1[:50])
print("Cipher2:",str2[:50])
print("Changes:",str3[:50])