In the Diffie-Hellman method Bob passes \(G^x\pmod p\) and Alice passes \(G^y\pmod p\), and where \(x\) and \(y\) are secrets. Let's say now that Alice wants Bob to prove that he still knows \(x\) without revealing his value. We can do this with Zero-knowledge proofs. In this case Bob produces a secret, a challenge, and a response, which Alice can check. Overall she never knows the value of \(x\) that Bob has used:
Diffie-Hellman with Zero-Knowledge Proof |
Theory
Within the Diffie-Hellman method, Bob and Alice generate random values (x and y):
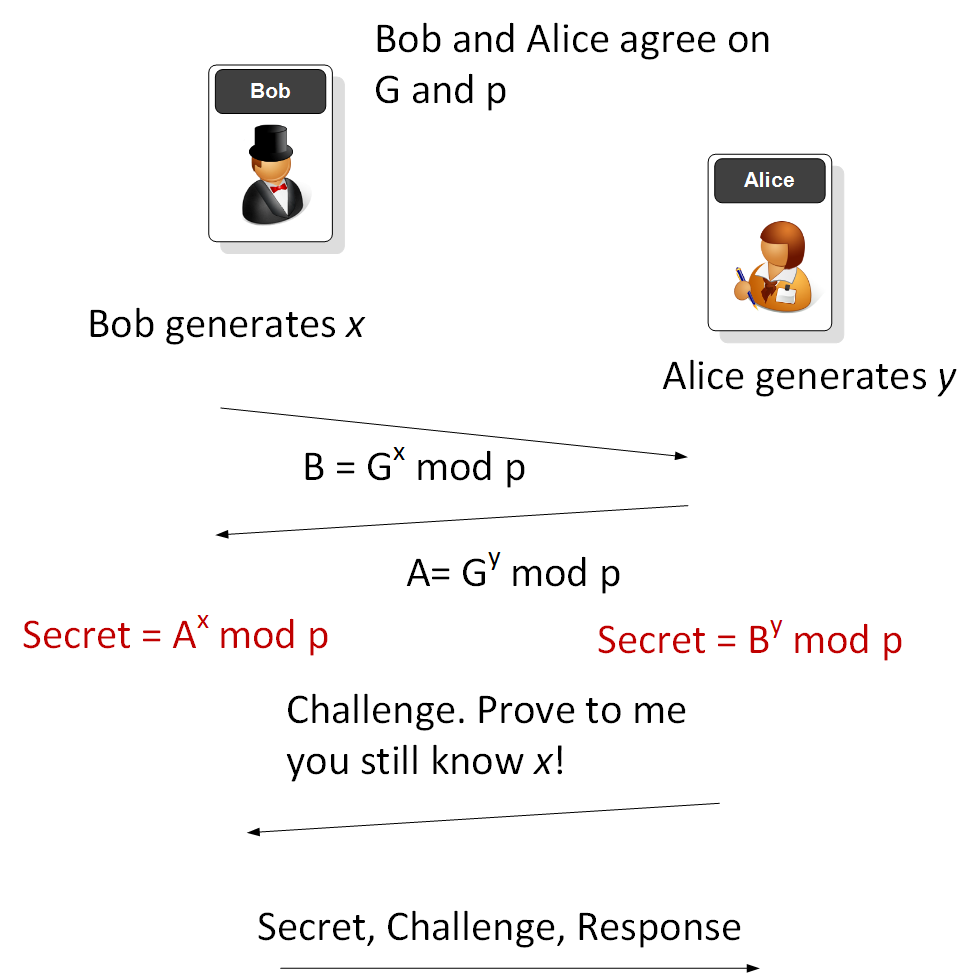
In this method we create a challenge and a response:
secret = self.get_shared_secret(remote_pub)
# Random key in the group Z_q
randKey = DiffieHellman() # random secret
commit1 = randKey.public
commit2 = randKey.get_shared_secret(remote_pub)
# shift and hash
concat = str(G) + str(prover_pub) + str(remote_pub) + str(secret) + str(commit1) + str(commit2)
h = hashlib.md5()
h.update(concat.encode("utf-8"))
challenge = int(h.hexdigest(), 16)
product = (self.secret * challenge) % phi
response = (randKey.secret - product) % phi
and where the challenge is a hash of G, the provers public key, the remote public key, the secret key, a random value and a shared secret random value. PHI is p-1.
In this case secret will be the shared secret that has been negotiated by Bob and Alice.
Code
We can use the code from [here to generate the secret, challenge and response:
import diffie
import sys
x=3
y=4
a = diffie.DiffieHellman(x)
b = diffie.DiffieHellman(y)
print("G=",a.G)
print("p=",a.P)
print("x=",x)
print("y=",y)
print("\n============")
print("a (pub,sec)=",a.public,a.secret)
print("b (pub,sec)=",b.public,b.secret)
shared=a.get_shared_secret(b.public)
print("Shared=",shared)
print("\nNow Bob will generate the secret, a challenge and a response")
results = a.prove_shared_secret(b.public)
print("(secret, challenge, response):",results)
val=a.verify_shared_secret(a.public, b.public, results[0], results[1], results[2])
print("\nAlice now checks")
if (val==shared):
print("Bob has proven he knows x")
else:
print("Bob has not proven that he knows x")
The code for diffie.py is:
import random
import hashlib
# DiffieHellman class enables construction of keys capable of performing
# D-H exchanges, and interactive proof of knowledge
class DiffieHellman:
P = 101
G = 51
def __init__(self,secret=0):
self.secret = random.randrange(1 << (self.G.bit_length() - 1), self.G - 1)
self.public = pow(self.G, self.secret, self.P)
def prove_shared_secret(self, remote_pub):
G = self.G; prover_pub = self.public; phi = self. P - 1;
secret = self.get_shared_secret(remote_pub)
# Random key in the group Z_q
randKey = DiffieHellman() # random secret
commit1 = randKey.public
commit2 = randKey.get_shared_secret(remote_pub)
# shift and hash
concat = str(G) + str(prover_pub) + str(remote_pub) + str(secret) + str(commit1) + str(commit2)
h = hashlib.md5()
h.update(concat.encode("utf-8"))
challenge = int(h.hexdigest(), 16)
product = (self.secret * challenge) % phi
response = (randKey.secret - product) % phi
return (secret, challenge, response)
def get_shared_secret(self, remote_pub):
return pow(remote_pub, self.secret, self.P)
# Verifies proof generated above. Verifier c is showing that
# shared secret between A and B was generated by A.
# returns 0 if if verification fails; returns shared secret otherwise
def verify_shared_secret(self, prover_pub, remote_pub, secret, challenge,
response):
P = self.P; G = self.G ; public = self.public
# g^r * (a's public key)^challenge
commit1 = (pow(G, response, P) * pow(public, challenge, P)) % P
# (b's public key)^response * (secret)^challenge
commit2 = (pow(remote_pub, response, P) * pow(secret, challenge, P)) % P
# Shift and hash
hasher = hashlib.md5()
concat = str(G) + str(prover_pub) + str(remote_pub) + str(secret) + str(commit1) + str(commit2)
hasher.update(concat.encode("utf-8"))
check = int(hasher.hexdigest(), 16)
if challenge == check:
return secret
else:
return 0