The Dragonfly zero-knowledge proof method is used in WPA-3 for Simultaneous Authentication of Equals (SAE):
Dragonfly Protocol - Zero Knowledge Proof |
Theory
Security in Wi-Fi has had a difficult route. In its current form (WPA-2) a password can be cracked by listening to the 4-way handshake between a client and the access point. This will then crack all the keys that have been used or will be used in the future. WPA-3 addresses this by securing the password, and uses zero-knowledge proof to make sure that no elements of the password are transmitted over the network. Both sides then pass their knowledge of the password, and then both can prove that each of them knows the secret password.
With WPA-2 we hash the SSID and the password and use this to create a master key (and which is used to derive session keys). The intruder can then use a dictionary or a brute force attack on the hash to discover the password and thus the long-term key (to which all other keys are derived). A PBKDF2 hash is used to make the hash difficult to crack, but if an intruder has GPU crackers, it can make the cracking fairly inexpensive. A weak password is also easily crackable, especially if it comes from a standard dictionary. This happens for an offline crack, and where an intruder can use Cloud-based crackers to crack the password on the system, and then crack all the keys derived from it.
The upgrading of wi-fi security has often been driven more by keeping compatibility with legacy devices than in driving forward improvements. With WEP we had a standard which broke almost every rule in the good cryptography book. It had a small IV value (24-bits), and which meant that it rolled-over after a relatively show time. This then cracked the global key for the whole network, and an intruder could listen to all of the encrypted traffic. It also supports a flawed stream cipher and key size: 40-bit RC4.
So the fix was WPA which integrated a new encryption method (TKIP) and where the IV and key size was increased to safer levels. In 2004, WPA-2 brought a block cipher: AES and improved authentication, and introduced the 4-way handshake. This handshake has since been the source of a number of vulnerabilities.
So with WPA-2 (802.11i) seen as flawed, the Wi-Fi Alliance has released WPA-3 [here], and which introduces almost seamless protection against brute-force attacks for network passwords. The protection only allows for one change to crack a password. As with WPA-2, it is available in two forms:
- WPA3-Personal: This replaces the 4-way handshake with Simultaneous Authentication of Equals (SAE) [1] and which is defined in the IEEE 802.11s standard. SAE was initially defined for mesh networks, but is now scaling to infrastructure wireless networks.
- WPA3-Enterprise: This integrates a back-end authentication infrastructure, such as with a RADIUS server. Elliptic Curve Diffie-Hellman (ECDH) exchange and Elliptic Curve Digital Signature Algorithm (ECDSA) using a 384-bit elliptic curve are used to a strong authentication.
Along with these changes, WPA-3 brings the integration of QR codes to gain the network connection details.
The focus for Simultaneous Authentication of Equals (SAE) is to properly authenticate a device onto a network and using a password and MAC addresses to authenticate. An intruder should not be able to connect to a network unless they known password that the access point uses. Also, an intruder should not be able to guess either the password or the long-term authentication element of the password. In WPA-2 an intruder can listen to the 4-way handshake and can then brute force the password from hashed value created (see the section below for details).
With SAE — and which is based on a zero-knowledge proof known as dragonfly — we use the Diffie-Hellman key exchange method but adds an authentication element. With this we create a shared key with elliptic curve methods (NIST curves), and then use a pre-shared key and MAC addresses. When the client connects to the access point, they perform an SAE exchange. If successful, they will each create a cryptographically strong key, of which the session key will be derived from. If one session key is cracked it will only affect one key, and not all of the key used, as with WPA-2.
Basically a client and access point goes into phases of commit and then confirm. Once we have a commitment, the client and access point can then go into the confirm states each time there is a session key to be generated. The method uses forward secrecy, where an intruder could crack a single key, but not all of the other keys.
In the commit phase, Alice (the client) generates two random values (a,A), then computes a scalar value (a+A). The value that Alice will pass is the PE (Password Equivalent — such as hashed value of the password that Bob and Alice know) raised to the power of -A. The operations are done with (mod q) and where q is a large prime number. Bob does the same, and then they exchange values. In the end they will have the same shared commit key (PE^{ab}). The password has been used to validate Bob and Alice, and they will only have the shared shared commit value if they both have the same password. The intruder cannot determine either the original password or the final shared value.
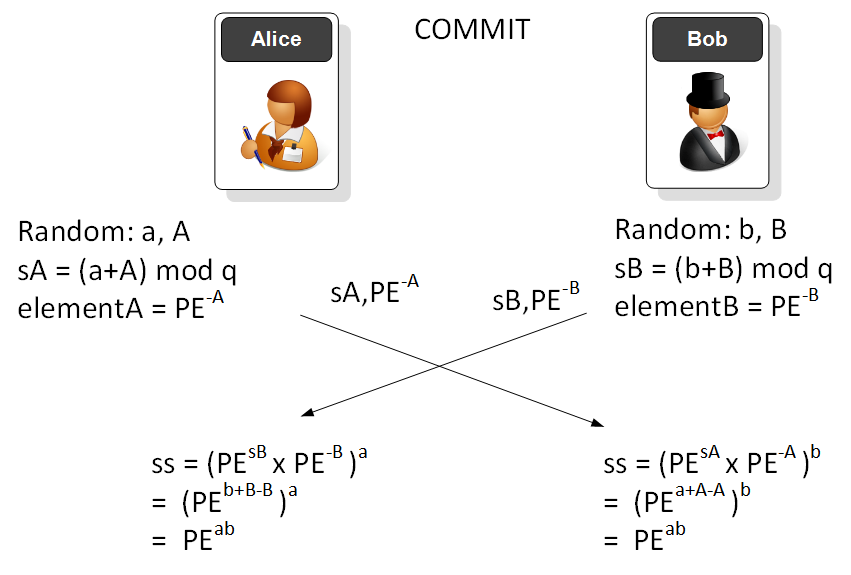
To perform the -A power, we perform an inverse mod q function:
elementA = inverse_of(pow(PE,A),q) elementB = inverse_of(pow(PE,B),q)
In the confirm phase we then use the long-term key to generate a unique session key. An attacker cannot determine the password used or the long-term master key (PMK). The cracking of one session key will not reveal the rest of the keys which have been used. Which is not the case for WPA-2.
Here is a simple implementation of the Dragon method:
import hashlib
import random
import sys
import libnum
q=131
text="hello"
a=random.randint(1,1000)
b=random.randint(1,1000)
A=random.randint(1,1000)
B=random.randint(1,1000)
sA= a + A
sB = b + B
PE = int(hashlib.md5(text.encode()).hexdigest()[:8], 16)
elementA = libnum.invmod(pow(PE,A),q)
elementB = libnum.invmod(pow(PE,B),q)
PEsA = pow(PE,sA,q)
PEsB = pow(PE,sB,q)
print("Password:",text)
print("Alice generates two random values")
print("a:\t",a)
print("A:\t",A)
print("\nBob generates two random values")
print("b:\t",b)
print("B:\t",B)
print("\nAlice calculates elementA")
print("Element A:",elementA)
print("\nBob calculates elementA")
print("Element B:",elementB)
ss1 = pow(PEsA * elementA,b,q)
ss2 = pow(PEsB * elementB,a,q)
print("\nThey exchange values and calculate a secret share")
print("\nAlice share:\t",ss1)
print("Bob share:\t",ss2)
A sample run is:
Password: hello Alice generates two random values a: 588 A: 352 Bob generates two random values b: 530 B: 718 Alice calculates elementA Element A: 212 Bob calculates elementA Element B: 112 They exchange values and calculate a secret share Alice share: 419 Bob share: 419