The Dual EC method is a random number generator which using an Elliptic Curve method. In the following we will take a random seed, and then generate 20 random values. With this method we have forward secrecy, and where it is not possible to determine the previous states from the current one:
Dual EC |
Theory
With Elliptic Curve methods, we take an elliptic curve (\(y^2=x^3+ax+b\)), and then use a base point (\(G\)). Next we generate a random number (\(n\)) and determine a point (\(P\)) by adding the point \(n\) times (\(G+G ... +G\)). We represent this as:
\(P = n G\)
The point \(P\) is our public key, and \(n\) is our private key. With current computing power, we cannot determine \(n\), even if we know \(P\) and \(G\) — as it known as the Elliptic Curve Discrete Logarithm Problem (ECDLP).
A core part of encryption is the generation of random numbers, as they are often used to create keys and salt values. If they can be guessed, it would break the whole foundation of cryptography, and significantly weaken the core of our security infrastructure. And so some thought that the NSA set out to create a backdoor function of the generation of random numbers, and that only they could break. Along the way they are alleged to have paid RSA Security $10 million to push the method (and also for its integration into the BSAFE library).
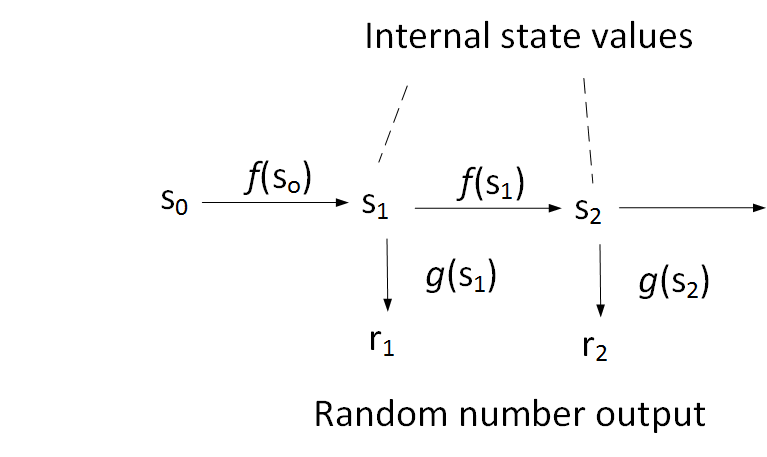
The method first appeared as a standard in 2006 when NIST and the ISO pushed it for adoption in the world-wide community, but, in 2007, researchers at Microsoft discovered a backdoor function. The basis of the method is to use an initial seed (\(s_0\)) and then use a function f to convert into a state value (\(s_1\)). This state value is then converted in a random output value using a function \(g\). The \(f\) and \(g\) functions are one way functions and cannot be reversed back:
But did the NSA place a backdoor into the method? With the Dual EC method, we use elliptic curve method to derive the functions. Initially we take a salt value (\(s_0\)) and then multiply it with a known point (\(P\)) to produce \(s_1\), and then take the x co-ordinate point. The first random value is the x-co-ordinate point of \(s_1\) times \(Q\) (another known point on the elliptic curve). This then continues as before:
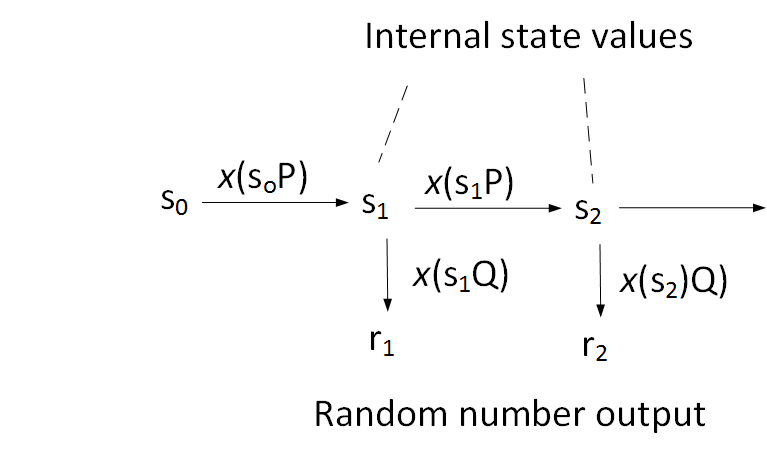
The curve in the NIST standard was the P-256 curve, and NIST published pre-defined values of \(P\) and \(Q\). This was highly unusual, as normally we would pick these values. People like Bruce Schneier just didn’t like the approach, and criticised it in 2007. The values selected for the P-256 curve were:
p256_Px = 6b17d1f2e12c4247f8bce6e563a440f277037d812deb33a0f4a13945d898c296 p256_Py = 4fe342e2fe1a7f9b8ee7eb4a7c0f9e162bce33576b315ececbb6406837bf51f5 p256_Qx = c97445f45cdef9f0d3e05e1e585fc297235b82b5be8ff3efca67c59852018192 p256_Qy b28ef557ba31dfcbdd21ac46e2a91e3c304f44cb87058ada2cb815151e610046
Some sample Go code from [here] can generate 20 random numbers:
package main
import (
"fmt"
"github.com/46bit/pnc"
"github.com/46bit/pnc/ec"
"crypto/rand"
"encoding/hex"
)
const (
dual_ec_drbg_curve_p256_qx = "c97445f45cdef9f0d3e05e1e585fc297235b82b5be8ff3efca67c59852018192"
dual_ec_drbg_curve_p256_qy = "b28ef557ba31dfcbdd21ac46e2a91e3c304f44cb87058ada2cb815151e610046"
)
func randomHex(n int) (string, error) {
bytes := make([]byte, n)
if _, err := rand.Read(bytes); err != nil {
return "", err
}
return hex.EncodeToString(bytes), nil
}
func main() {
randval,_ := randomHex(20)
s0 := ec.NewBigInt(randval, 16)
curve := ec.NewP256Curve()
r := pnc.NewDualECDRBG(
curve,
ec.NewBigInt(dual_ec_drbg_curve_p256_qx, 16),
ec.NewBigInt(dual_ec_drbg_curve_p256_qy, 16),
s0)
fmt.Printf("Seed: %s\n", randval)
for i := 0; i < 20; i++ {
fmt.Printf("%d\t%x\n", i, r.Bytes(4))
}
}
A sample run gives:
0 c15e8bae 1 5a85400b 2 50b9054b 3 f44b3267 4 bb1a07c7 5 2d27a8da 6 c14c4dde 7 3e12efe8 8 6d97bd2a 9 cc630ed1 10 4a3f0cf1 11 155aa6ad 12 53dd33bd 13 4d7c0a14 14 401f83bc 15 a78cfb43 16 97765f8c 17 565cf6cd 18 86667707 19 5257d96e
But the researchers at Microsoft — Dan Shumow and Niels Ferguson — noticed a flaw in this. They couldn’t understand why users couldn’t just pick their own \(P\) and \(Q\) points. So, they posed, “what happens when \(P = d Q\), and where \(d\) is known by an adversory?” Then if we recover the y co-ordinate point for the random value we get \(R_1\). If we multiply the random value (\(R_1\)) by \(d\) we get:
\(d (R_1) = d (s_1 Q) = s_1 (d Q) = s_1 P\)
and we have discovered the internal state of the random number generator (\(s_1 P\)), and an adversary can then derive all the other random numbers from here.
At the time, RSA refuted claims that it intentionally put in the backdoor:
We made the decision to use Dual EC DRBG as the default in BSAFE toolkits in 2004, in the context of an industry-wide effort to develop newer, stronger methods of encryption. At that time, the NSA had a trusted role in the community-wide effort to strengthen, not weaken, encryption. When NIST issued new guidance recommending no further use of this algorithm in September 2013, we adhered to that guidance, communicated that recommendation to customers and discussed the change openly in the media.
And so while Snowden perhaps revealed the NSA knew about the backdoor, others, such as Michael Wertheimer (NSA Director of Research), gave a different viewpoint:
During the development of the ANSI standard based on the NIST publication, members of X9F1 (the ANSI-approved working group responsible for cryptographic tools) raised concerns about the potential that elliptic curve points used as parameters for the Dual_EC_DRBG could harbor a trapdoor secret known only to, and exploitable only by, the person who generated the points. As a result, the X9F1 committee expanded the standard to include verifiable random point generation. Since the NSA was using the algorithm at the time and had generated elliptic curve points for protecting Department of Defense users, the NSA-generated points were included in the standard. In other words, any implementation that used the NSA-generated points would be deemed compliant. Shortly thereafter, NIST negotiated with ANSI to use the ANSI Random Number Generation Standard as the basis for an NIST Random Number Generation Standard. ANSI also approved submitting a version of this standard to the ISO.