For a finite field elliptic curve we have for a curve of \(y^2 = x^3 + ax +b\) and for a defined prime number (\(p\)). If we have a point \(P\), we can then calculate \(2P\) (and use this to find \(nP\) - where \(n\) is the number of times we add \(P\)). In this case we will define an x-point on the curve and determine its y co-ordinate and nP [Real curves]. We then add the point \(n\) times:
Finding nP when we have P for EC |
Coding
In this case we calculate \(x^3+ax+b \pmod p\). For point addition of \(P\) (\(x,y\)) we calculate the point addition for a given point (\(P+P\)) and represent it by (\(2P\)). For this we have:
\(2P = (x_2, y_2)\)
Let \(s = (3x^2 + a)/(2y)\)
Then:
\(x_2 = s^2 - 2x\)
\(y_2 = s(x - x_2) - y\)
We can add two points \((x_1,y_1)\) and \((x_2,y_2)\):
Let \(s = (y_1-y_2)/(x_1-x_2)\)
Then:
\(x_2 = s^2 - x_1 - x_2\)
\(y_2 = s(x_1 - x_2) - y_1\)
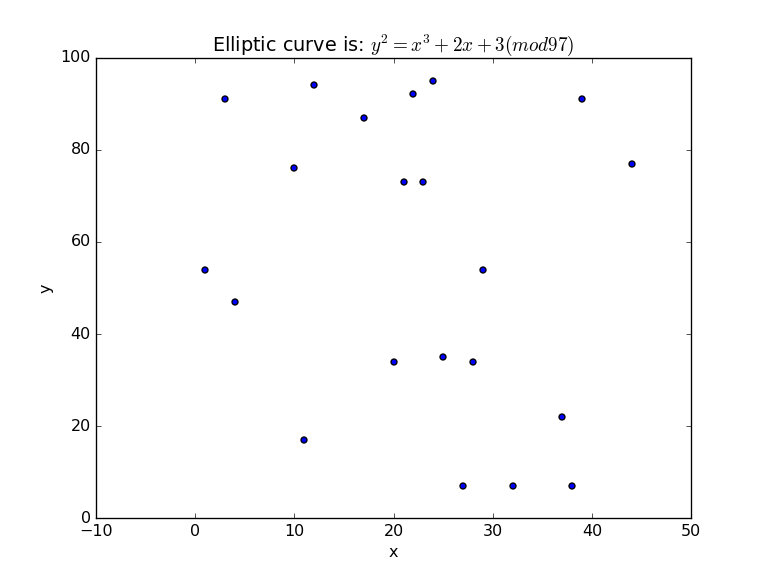
In ECC, we have an equation of y²=x³+ax+b (mod p). This gives us points on an elliptic curve. For a=2, b=3 and p=97, we get [here]:
(1, 54) (3, 91) (4, 47) (10, 76) (11, 17) (12, 94) (17, 87) (20, 34) (21, 73) (22, 92) (23, 73) (24, 95) (25, 35) (27, 7) (28, 34) (29, 54) (32, 7) (37, 22) (38, 7) (39, 91) (44, 77) (46, 72) (47, 79) (49, 34) (50, 19) (52, 68) (53, 73) (54, 85) (55, 91) (56, 89) (59, 65) (65, 65) (67, 54) (70, 65) (73, 83) (74, 77) (76, 77) (80, 87) (83, 74) (84, 37) (85, 26) (86, 69) (87, 27) (88, 41) (91, 39) (92, 81) (95, 66)And a basic plot is [here]:
For public key encryption we must create a base point (G), and then add it n times (to get nG). The value of nG will be our public key, and the value of n will be our private key. But how do we choose a base point? Let's try (3,91):
a= 2 b= 3 p= 97 n= 18 x-point= 3 P (3,91) Point is on curve 2P (80,87) Point is on curve 3P (80,10) Point is on curve 4P (3,6) Point is on curve 5P=0 6P (3,91) Point is on curve 7P (80,87) Point is on curve 8P (80,10) Point is on curve 9P (3,6) Point is on curve 10P=0 11P (3,91) Point is on curve 12P (80,87) Point is on curve 13P (80,10) Point is on curve 14P (3,6) Point is on curve 15P=0 16P (3,91) Point is on curve 17P (80,87) Point is on curve 18P (80,10) Point is on curve
We can see that this is a bad base point, as it will cycle. We define the order of this point (N) as N=5. We define this as the subgroup generated by P has 5 points. Now let's try a base point of (1,54) [here]:
a= 2 b= 3 p= 97 n= 18 x-point= 1 P (1,54) Point is on curve 2P (92,81) Point is on curve 3P (0,87) Point is on curve 4P (21,24) Point is on curve 5P (53,24) Point is on curve 6P (65,65) Point is on curve 7P (85,71) Point is on curve 8P (46,72) Point is on curve 9P (23,73) Point is on curve 10P (3,6) Point is on curve 11P (87,70) Point is on curve 12P (52,29) Point is on curve 13P (47,18) Point is on curve 14P (74,20) Point is on curve 15P (88,41) Point is on curve 16P (32,90) Point is on curve 17P (17,87) Point is on curve 18P (95,31) Point is on curve
And we can see that (1,54) makes a much better base point, as it does not cycle for the range of n values that we have chosen. In fact, in this case, subgroup generated by P has 50 points.
43P (85,26) Point is on curve 44P (65,32) Point is on curve 45P (53,73) Point is on curve 46P (21,73) Point is on curve 47P (0,10) Point is on curve 48P (92,16) Point is on curve 49P (1,43) Point is on curve 50P=0 51P (1,54) Point is on curve 52P (92,81) Point is on curve 53P (0,87) Point is on curve 54P (21,24) Point is on curve
So, in real-life, when we select a base point, we make sure that it has a high order value, so that it does not cycle. For SEPC256k1, we have a base point and prime number of:
x = 0x79BE667EF9DCBBAC55A06295CE870B07029BFCDB2DCE28D959F2815B16F81798
y = 0x483ADA7726A3C4655DA4FBFC0E1108A8FD17B448A68554199C47D08FFB10D4B8
p = 0xFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFEFFFFFC2F
The order is:
N = FFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFEBAAEDCE6AF48A03BBFD25E8CD0364141
The value of N will thus give us our core security levels, and will define the number of possible values before we cycle.
Coding
The coding is:
import sys
import libnum
a=0
b=7
p=37 # prime number
n=10 # number of points to show
x=3 # starting point
if (len(sys.argv)>1):
x=int(sys.argv[1])
if (len(sys.argv)>2):
p=int(sys.argv[2])
if (len(sys.argv)>3):
a=int(sys.argv[3])
if (len(sys.argv)>4):
b=int(sys.argv[4])
if (len(sys.argv)>5):
n=int(sys.argv[5])
print("a=",a)
print("b=",b)
print("p=",p)
print("n=",n)
print("x-point=",x)
if (n>20): n=20
z=(x**3 + a*x +b) % p
if (libnum.has_sqrtmod(z,{p:1} )):
y=next(libnum.sqrtmod(z,{p:1}))
print("P\t(%d,%d)" % (x,y), end=' ')
if ((y**2 % p) == ((x**3+a*x+b) %p)): print(" \tPoint is on curve")
else:
print(" \tPoint is not on curve")
sys.exit()
s=((3*x**2)+a) * libnum.invmod(2*y,p)
x1=(s**2-2*x) % p
y1=((s*(x-x1))-y) % p
x3=x1
y3=y1
x2=0
y2=0
counter=1
for i in range(2, n+1):
counter=counter+1
if (counter>n): sys.exit()
print("%dP\t(%d,%d)" % (counter,x1,y1), end=' ')
if ((y1**2 % p) == ((x1**3+a*x1+b) %p)): print(" \tPoint is on curve")
rtn=libnum.invmod(x1-x,p)
if (rtn==0):
print("%dP=0" % (counter+1))
counter=counter+2
s=((3*x**2)+a) * libnum.invmod(2*y,p)
x1=(s**2-2*x) % p
y1=((s*(x-x1))-y) % p
print("%dP\t(%d,%d)" % (counter,x,y), end=' ')
if ((y**2 % p) == ((x**3+a*x+b) %p)): print(" \tPoint is on curve")
else:
s=(y1-y)* rtn
x2=(s**2-x1-x) % p
y2=((s*(x1-x2)-y1)) % p
x1=x2
y1=y2
A sample run for a point of (3,16), and where we can generate all 18 points within the finite field:
a= 0 b= 7 p= 37 n= 18 x-point= 3 P (3,16) Point is on curve 2P (35,31) Point is on curve 3P (8,36) Point is on curve 4P (5,13) Point is on curve 5P (22,31) Point is on curve 6P (24,20) Point is on curve 7P (17,6) Point is on curve 8P (16,25) Point is on curve 9P (6,36) Point is on curve 10P (19,13) Point is on curve 11P (12,25) Point is on curve 12P (23,1) Point is on curve 13P (0,28) Point is on curve 14P (13,24) Point is on curve 15P (32,20) Point is on curve 16P (30,16) Point is on curve 17P (4,21) Point is on curve 18P (18,20) Point is on curve
Presentation
The following is a presentation: