For a finite field elliptic curve we can search for the first 100 points for a curve of \(y^2 = x^3 + ax +b\) and for a defined prime number (\(p\)):
First 20 Elliptic Curve Points |
Background
We love things that are beautifully crafted and design. Unfortunately the world of cybersecurity is often tainted by cybercriminals, Tor networks hiding drug dealing, and cryptocurrency mining on our computers. But there is beauty to be found, and that beauty lies in the heart of elliptic curve cryptography (ECC). While some may want to spy on your every on-line action, it is ECC that is currently holding up our rights to privacy, and to properly identity our transactions and our identities.
Few things in this world holds up our rights than ECC.
You must thus thank ECC whenever you connect to your corporate wifi network, or to your VPN server in your local coffee shop. Behind them is ECC working hard in generating a new encryption key every time you connect to a Web site (ECDH), and leaving those who want to spy on us scratching their heads. And for our transactions, it is ECC again which makes sure that we properly identity senders and receivers. ECC cares little for a world build with false trust identities — such as with IBAN and CVV2 numbers — and signs for things with true digital trust.
And so we end up with these values that define an elliptic curve (p,a,b,gx,gy,n), and where a and b are the values used in:
\(y^2 = x^3+ax +b \pmod p\)
All our operations are performed with (mod p), and where (\(g_x,g_y\)) is a base point on our curve.
If we plot our equation of y² = x³ +7, we get a nice curve of:
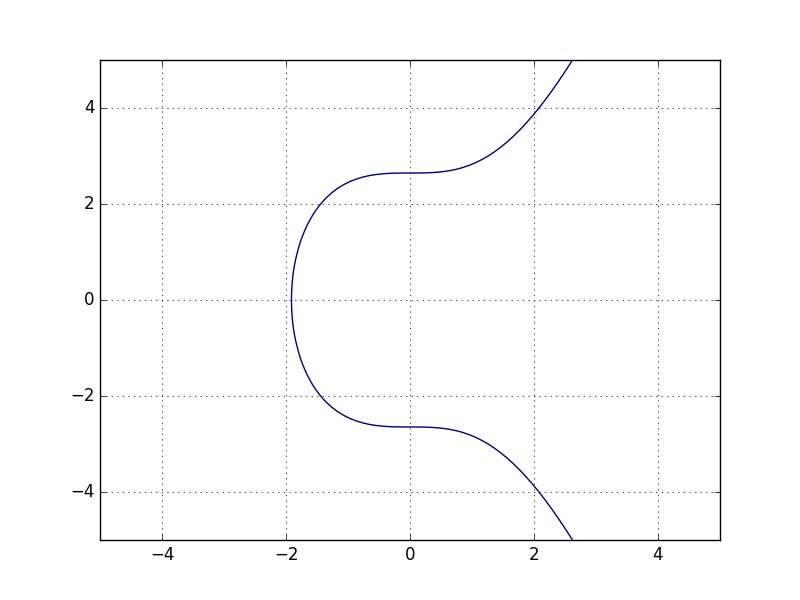
But, wait, we also have (mod p), and where we use a prime number. So let’s give these a go. First with a prime of 23:
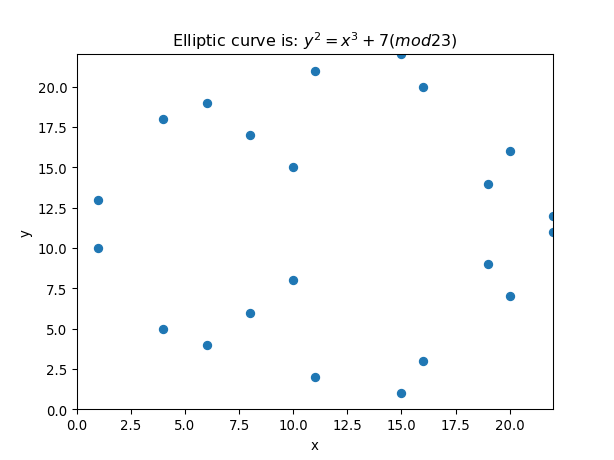
The points we get are [ink]:
(1,13) (1,10) (4,18) (4,5) (6,4) (6,19) (8,6) (8,17) (9, 0) (10,8) (10,15) (11,2) (11,21) (15,1) (15,22) (16,3) (16,20) (19,9) (19,14) (20,16) (20,7) (22,12) (22,11)
Now we can see that there is not an x-value for every y, as we need to find an integer which matches a square root of a mod value:
\(y^2 = val \pmod p\)
In the case of \(x=1\) gives \(1^3+7=8\), and \(13^2 \pmod {23}=8\).
Coding
The outline code is:
import sys
import matplotlib.pyplot as plt
file='1111'
p=23
startval=1
a=0
b=7
if (len(sys.argv)>1):
p=int(sys.argv[1])
if (len(sys.argv)>2):
a=int(sys.argv[2])
if (len(sys.argv)>3):
b=int(sys.argv[3])
if (len(sys.argv)>4):
file=str(sys.argv[4])
def modular_sqrt(a, p):
""" Find a quadratic residue (mod p) of 'a'. p
must be an odd prime.
Solve the congruence of the form:
x^2 = a (mod p)
And returns x. Note that p - x is also a root.
0 is returned is no square root exists for
these a and p.
The Tonelli-Shanks algorithm is used (except
for some simple cases in which the solution
is known from an identity). This algorithm
runs in polynomial time (unless the
generalized Riemann hypothesis is false).
"""
# Simple cases
#
if legendre_symbol(a, p) != 1:
return 0
elif a == 0:
return 0
elif p == 2:
return p
elif p % 4 == 3:
return pow(a, (p + 1) // 4, p)
# Partition p-1 to s * 2^e for an odd s (i.e.
# reduce all the powers of 2 from p-1)
#
s = p - 1
e = 0
while s % 2 == 0:
s /= 2
e += 1
# Find some 'n' with a legendre symbol n|p = -1.
# Shouldn't take long.
#
n = 2
while legendre_symbol(n, p) != -1:
n += 1
# Here be dragons!
# Read the paper "Square roots from 1; 24, 51,
# 10 to Dan Shanks" by Ezra Brown for more
# information
#
# x is a guess of the square root that gets better
# with each iteration.
# b is the "fudge factor" - by how much we're off
# with the guess. The invariant x^2 = ab (mod p)
# is maintained throughout the loop.
# g is used for successive powers of n to update
# both a and b
# r is the exponent - decreases with each update
#
x = pow(a, (s + 1) / 2, p)
b = pow(a, s, p)
g = pow(n, s, p)
r = e
while True:
t = b
m = 0
for m in range(r):
if t == 1:
break
t = pow(t, 2, p)
if m == 0:
return x
gs = pow(g, 2 ** (r - m - 1), p)
g = (gs * gs) % p
x = (x * gs) % p
b = (b * g) % p
r = m
def legendre_symbol(a, p):
""" Compute the Legendre symbol a|p using
Euler's criterion. p is a prime, a is
relatively prime to p (if p divides
a, then a|p = 0)
Returns 1 if a has a square root modulo
p, -1 otherwise.
"""
ls = pow(a, (p - 1) // 2, p)
return -1 if ls == p - 1 else ls
def findit(start,p,a,b):
xval=[]
yval=[]
x=start
count=0
while True:
val=((x*x*x) + a*x+ b) % p
if (val==0):
print(x,0)
rtn= legendre_symbol(val, p)
if (rtn==1):
res=modular_sqrt(val, p)
xval.append(x)
yval.append(int(res))
print ("(%d,%d)" % (x,res),end='')
xval.append(x)
yval.append(int(p-res))
print ("(%d,%d)" % (x,p-res),end='')
count=count+1
if (x>p-2 or x>200): return xval,yval
x=x+1
if (x-start>200): return xval,yval
return xval,yval
title=""
if (a==0):
title="Elliptic curve is: $y^2=x^3+"+str(b)+" (mod "+str(p)+")$"
else:
title="Elliptic curve is: $y^2=x^3+"+str(a)+"x+"+str(b)+ " (mod "+str(p)+")$"
print (title)
print()
xval,yval=findit(0,p,a,b)
plt.title(title)
plt.xlabel('x')
plt.ylabel('y')
plt.axis([0,max(xval),0,max(yval)])
plt.scatter(xval,yval)
my_dpi=96
f2= file+".svg"
plt.savefig(f2,format='SVG',dpi=my_dpi)
f2= file+".png"
plt.savefig(f2,format='PNG',dpi=my_dpi)
A version that uses libnum instead of the Python code is:
import sys
import matplotlib.pyplot as plt
from libnum import jacobi,has_sqrtmod,sqrtmod
file='1111'
p=23
startval=1
a=0
b=7
if (len(sys.argv)>1):
p=int(sys.argv[1])
if (len(sys.argv)>2):
a=int(sys.argv[2])
if (len(sys.argv)>3):
b=int(sys.argv[3])
if (len(sys.argv)>4):
file=str(sys.argv[4])
def modular_sqrt(y2,p):
if (has_sqrtmod(y2,{p:1})):
res=sqrtmod(y2,{p:1})
y=next(res)
return (y)
def findit(start,p,a,b):
xval=[]
yval=[]
x=start
count=0
while True:
val=((x*x*x) + a*x+ b) % p
rtn= jacobi(val, p)
if (rtn!=-1):
res=modular_sqrt(val, p)
xval.append(x)
yval.append(int(res))
print ("(%d,%d)" % (x,res),end='')
xval.append(x)
yval.append(int(p-res))
print ("(%d,%d)" % (x,p-res),end='')
count=count+1
if (x>p-2 or x>200): return xval,yval
x=x+1
if (x-start>200): return xval,yval
return xval,yval
title=""
if (a==0):
title="Elliptic curve is: $y^2=x^3+"+str(b)+" (mod "+str(p)+")$"
else:
title="Elliptic curve is: $y^2=x^3+"+str(a)+"x+"+str(b)+ " (mod "+str(p)+")$"
print (title)
print()
xval,yval=findit(0,p,a,b)
plt.title(title)
plt.xlabel('x')
plt.ylabel('y')
plt.axis([0,max(xval),0,max(yval)])
plt.scatter(xval,yval)
my_dpi=96
f2= file+".svg"
plt.savefig(f2,format='SVG',dpi=my_dpi)
f2= file+".png"
plt.savefig(f2,format='PNG',dpi=my_dpi)
Presentation
The following is an outline: