With Fiat–Shamir we can prove that we know a value without actually revealing the orginal value. In the following Bob will prove to Alice that he still knows his password. Bob generates a random number (\(v\)) and computers a challenge value (\(c\)), and sends the proof that he still knows \(x\) [paper]:
Fiat–Shamir with Go and ECC (Non-interactive ZKP) |
Method
Why do give away your sensitive information? Why not register a version of your secret, and then just prove that you still know it. For this, we turn to Fiat-Shamir method. One way of implementing it is in discrete logarithms [here], but we can use something even more powerful ... elliptic curve cryptography. First Bob and Alice agree on two points on their selected elliptic curve (\(G\) and \(H\)). Next Bob, takes his secret and hashes it to produce a secret value (\(x\)). He then computes \(xG\) and \(xH\) (which is the points \(G\) and \(H\) added \(x\) times), and sends these to Alice. Alice then registers them:
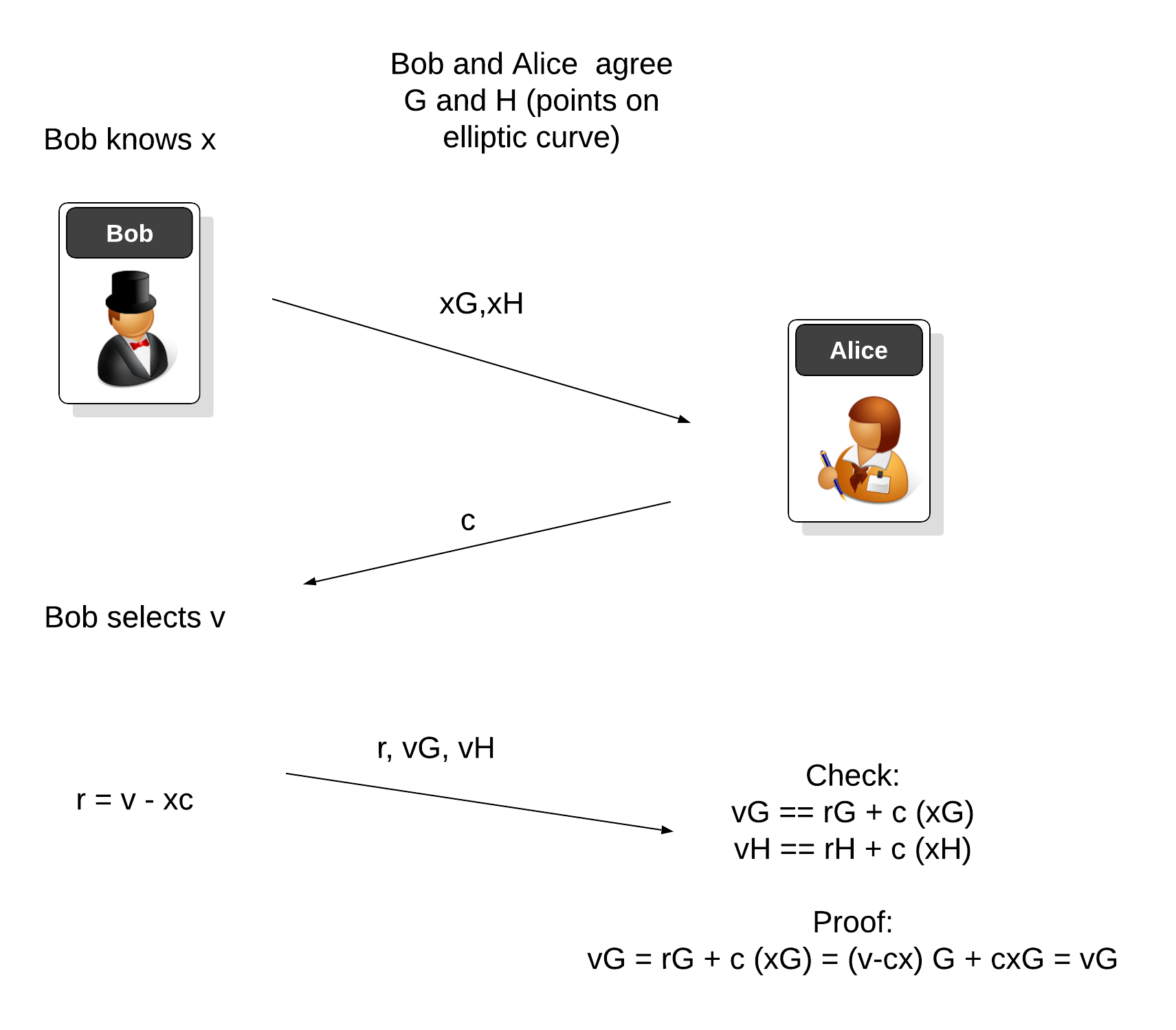
Next Alice sends a random challenge value (\(c\)) and sends this to Bob. Bob then generates his own random value (\(v\)), and computes \(r\):
\(r = v - cx\)
This is done as an elliptic curve multiply (\(cx\)) and subtract (\(v-cx\)). He also computes \(vG\) and \(vH\), and sends \(r\), \(vG\), and \(vH\) back to Alice. Alice then checks that:
\(vG\) is equal to \(rG + c(xG)\)
and
\(vH\) is equal to \(rH + c(xH)\)
If they are the same, Bob has proven his password!
In Go, we can convert our password (m) into a value by taking a hash of it (SHA-256):
message := []byte(m) scal := sha256.Sum256(message[:]) x := suite.Scalar().SetBytes(scal[:32])
Next we can generate our elliptic curve points (G and H):
G := suite.Point().Pick(rng) H := suite.Point().Pick(rng)
The values passed to Alice can be generated with:
xG := suite.Point().Mul(x, G) xH := suite.Point().Mul(x, H)
Bob can now generate a challenge, without requiring Alice to send it (non-interactive). For this Bob, takes a hash of \(xG\), \(xH\), \(vG\) and \(vH\):
h := suite.Hash()
xG.MarshalTo(h)
xH.MarshalTo(h)
vG.MarshalTo(h)
vH.MarshalTo(h)
cb := h.Sum(nil)
c := suite.Scalar().Pick(suite.XOF(cb))
Bob can then compute r, rG, and rH with:
r := suite.Scalar()
r.Mul(x, c).Sub(v, r)
rG := suite.Point().Mul(r, G)
rH := suite.Point().Mul(r, H)
Alice then checks:
cxG := suite.Point().Mul(c, xG)
cxH := suite.Point().Mul(c, xH)
a := suite.Point().Add(rG, cxG)
b := suite.Point().Add(rH, cxH)
fmt.Printf("Alice sends challenge:\n c: %s\n\n",c)
fmt.Printf("Bob computes:\n v:\t%s\n r:\t%s\n\n",v,r)
if !(vG.Equal(a) && vH.Equal(b)) {
fmt.Printf("Incorrect proof!")
} else {
fmt.Printf("Proof correct")
}
Code
Here is the code:
A sample run is:
Bob and Alice agree: G: 3fd96d7b139e8805e3d94f1e04cd637aae7b9c2565a708464b62449cbbfb07fa H: f7bf1938a30b2a84e745cbe96b25854be4a62ea69b936b8071bad412c89118f5 Bob's Password: qwerty Bob's Secret (x): 49f9c587f98c1e5840ee76f205437cf9a582b27168c0ea744b2cf58ee0233705 Bob sends these values: xG: b21b0fe0af6c874300fd3dcd95b6c7a2d98ef9014632661a9f86e16e134cbc0d xH 6d009dacea721114976c5da13fbe88afeaac8ff204dfdf73b6a5c4f9b1bb651e Alice sends challenge: c: 7592f5abb87a6797e6f63eb0a571a51a0197a258d25002079acd82e5dc9c990e Bob computes: v: 18025bbd0c975f8762a263603ab1c1887884e10a748a65b2f2a428a90994220f r: af90b47cf39b03966bd5003de377147c0103e4d22b424740a23dcd046057300e Proof correct
A presentation is: