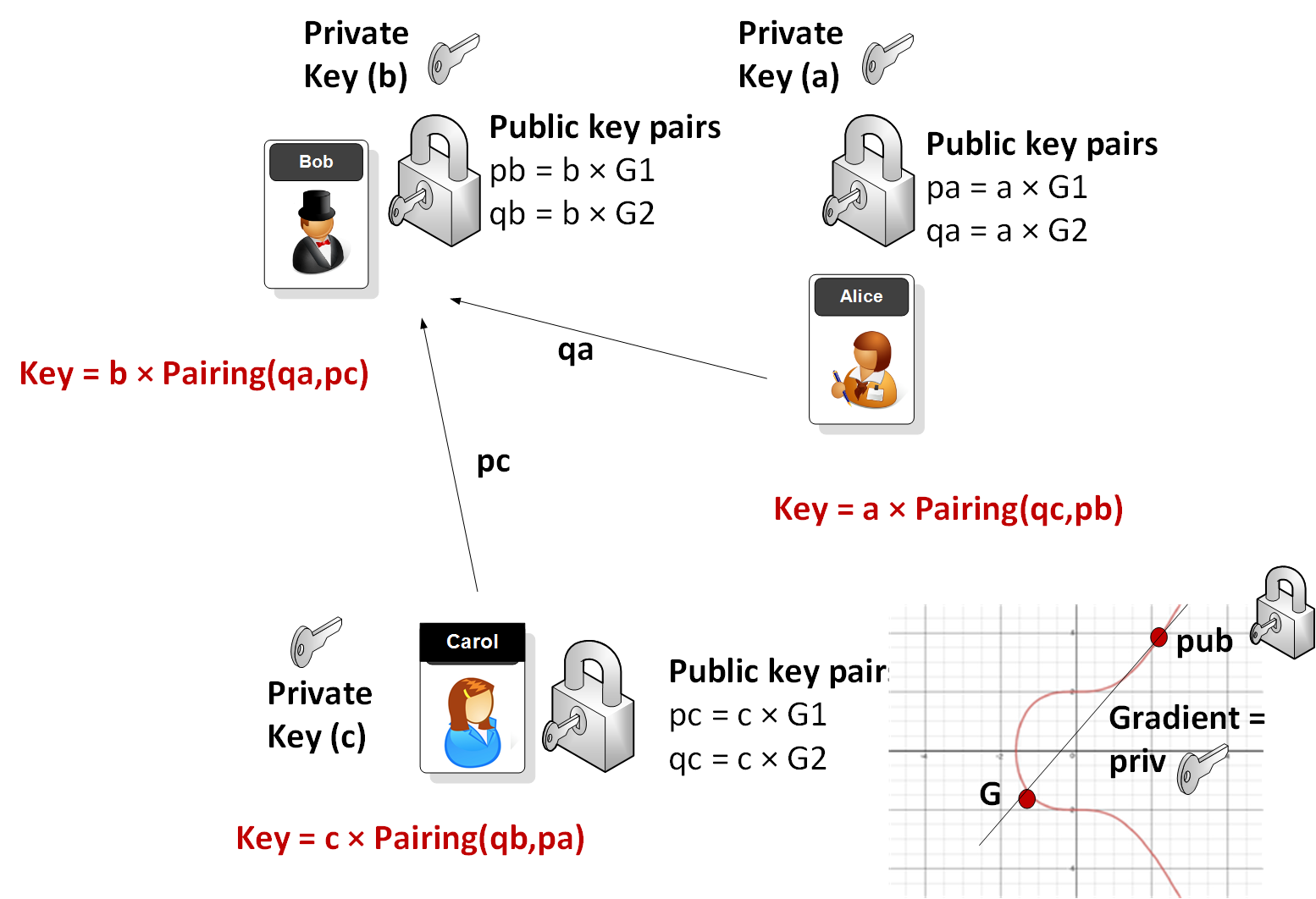
Elliptic curves are used fairly extensively in public key encryption (such as in Bitcoin and Tor). A BN-curve (Barreto-Naehrig curve) [paper] defines an elliptic curve which can be used for pairings that allow for a high security and efficiency level. So how do we generate a shared key between three parties? This page implements the tripartite Diffie-Hellman algorithm [Paper] and that Bob (B), Alice (A) and Carol (C) share their key pairings and then can calculate a shared secret key. In this case a, b and c are the private keys generated by Alice, Bob and Carol, respectively. Bob, Alice and Carol then generate public keys from curves G1 and G2. In this case we show the keys for Alice, which are pa (\(pa = a \times G1\)), and qa (\(qa = a \times G2\)). Alice then calculate the shared key by taking the public values passed from Bob and Alice, and then multiplying it by her secret key (a). In this case we will use the MIRACL Go library.
Tripartite Diffie-Hellman algorithm with MIRACL |
Theory
For an Elliptic Curve we generate a 256-bit random number for the private key (\(p\)), and then take a point (\(G\)) [x,y] on the Elliptic Curve and then multiply it by the private key to get another point \( (p \times x,p \times y)\). In this way we get \(P = p \times G\), and where \(G\) is a known point on the Elliptic Curve, \(P\) is our public key and \(p\) is our private key.
With pairings we can derive more complex relationships between the points, such as if \(P = G \times p\), \(Q = G \times q\) and \(R = G \times r\), we can check to see if \(r = p \times q \), but where we only know P, Q and R (the public values). At the current time we cannot compute \(p\) from \(P = p \times G\), even if we know \(P\) and \(G\). The exposure of the values is limited as we can calculate \(R = G \times p \times q\), and where it is not possible to determine \(p\) or \(q\).
Checking linear constraints
So let's say I want to prove to you that I know the proof for:
\(2 p + 3 q = 5 r\)
I can then give you \(p \times G + q \times G\) and \(r \times G\).
These values will be \(P\), \(Q\) and \(R\). Next you can check:
I can then give you \(2 P + 3 Q\) and \(5 R\).
If it is correct, I have proven that I know \(p\), \(q\) and \(r\).
The values we have used are defined for the pairing are defined as a bilinear map, and following this:
\(e(P, Q + R) = e(P, Q) \times e(P, R)\)
\(e(P + S, Q) = e(P, Q) \times e(S, Q)\)
Our focus for this is to be able to add, subtract, multiply and divide encrypted values.
With elliptic curve pairing we map \(G2 \times G1\) to \(Gt\) using:
- G1 and which is an elliptic curve for the equation \(y^2 = x^3 + b\) and includes the module of a prime number (N)
- G2 and which is an elliptic curve which have the same points as G1 and which fit values of \(w\)- a "magic number" - for \(w^{12} - 18 w^6 + 82 = 0\). I will describe this in another article.
- Gt and which is the resulting object.
Three-way handshake with BN pairings
The following code integrates with BN-256 code for the generation of a shared key between three parties (Bob, Alice and Carol). The pairings use two elliptic curves: G1 and G2. Each person will generate their public key from each of these curves. First Bob (B), Alice (A) and Carol (C) generate their private keys (a, b and c) and which are random numbers. Next they create their pairings (qa, pa), (qb, pb) and (qc, pc). These will be:
\(pa = a \times G1\)
\(qa = a \times G2\)
\(pb = b \times G1\)
\(qb = b \times G2\)
\(pc = c \times G1\)
\(qc = c \times G2\)
If we take the example of Bob, then he will receive qa from Alice and pc from Carol, and then create a pairing and multiple by his private key (b). The result is the shared key:
Coding
package main
import (
"fmt"
"math/rand"
"time"
"github.com/miracl/core/go/core/BN254"
)
func FP12toByte(F *BN254.FP12) []byte {
const MFS int = int(BN254.MODBYTES)
var t [12 * MFS]byte
F.ToBytes(t[:])
return(t[:])
}
func main() {
rand.Seed(time.Now().UnixNano())
a1:= rand.Intn(4294967296)
b1:= rand.Intn(4294967296)
c1:= rand.Intn(4294967296)
a := BN254.NewBIGint(a1)
b := BN254.NewBIGint(b1)
c := BN254.NewBIGint(c1)
P := BN254.ECP_generator()
P2 := BN254.ECP2_generator()
pa:=BN254.G1mul(P,a)
qa:=BN254.G2mul(P2,a)
pb:=BN254.G1mul(P,b)
qb:=BN254.G2mul(P2,b)
pc:=BN254.G1mul(P,c)
qc:=BN254.G2mul(P2,c)
k1 := BN254.Ate(qb,pc)
k1 = BN254.Fexp(k1)
k1 = BN254.GTpow(k1, a)
k2 := BN254.Ate(qc,pa)
k2 = BN254.Fexp(k2)
k2 = BN254.GTpow(k2, b)
k3 := BN254.Ate(qa,pb)
k3 = BN254.Fexp(k3)
k3 = BN254.GTpow(k3, c)
fmt.Printf("a: %d\n",a1)
fmt.Printf("b: %d\n",b1)
fmt.Printf("c: %d\n",c1)
fmt.Printf("Key: %s\n",k1.ToString())
fmt.Printf("K1 (Alice) - first 20 bytes:\t0x%x\n",FP12toByte(k1)[:20])
fmt.Printf("K2 (Bob) - first 20 bytes:\t0x%x\n",FP12toByte(k2)[:20])
fmt.Printf("K3 (Carol) - first 20 bytes:\t0x%x\n",FP12toByte(k3)[:20])
if k1.Equals(k2) { fmt.Printf("\nK1 is equal to K2")}
if k2.Equals(k3) { fmt.Printf("\nK2 is equal to K3")}
if k1.Equals(k3) { fmt.Printf("\nK1 is equal to K3")}
}
Sample run
a: 2719126188 b: 726866828 c: 1018051739 Key: [[[21be3464f65effed102b3a64e941604e09bb9b73c0c6747fbfbefac008362c94,05dd4316f1a38529f107540fe3dd478a82bd25530775c3faffd2c6635b0b7a82],[0753e6b49d30c676b2ee5d3aa6fc63d3b3f81b20e2c6a67d66f694879d339075,17475b7cb8210b477c94e5da73d6f873d84df5434ae056d322c6da177aa3ffbb]],[[0b5db416cfafc58600c1e4987e82732bc7286fe23be7d22508cb64d955295ce1,18dda8578cb1eb032d0ca6920bda7f26e9f856a78cc0d51232d6806e2945a218],[2458c39bcf30548b07a67b61da1389baed94809de97a3cd206d4012d499e2518,13ea26d6c484c33f9c9cecb4b8a2262212889d774885886d02b0d41724573897]],[[0f11cbb0012665905fb30a4b8319c2e33e5a3abdba1f4764b3cb78999213830e,186971c1b7b716de42585e0b464bd2790956d45bb2007fa952e203fc1dfd4d10],[19854d4347dd16dc1ed869e1e0f25436cd43963c935645b74b02fde429ab737b,0bfa91a65df99e5cd6baf6ebd969c1c106aff26f84cbffd45954ed0f4bbd076b]]] K1 (Alice) - first 20 bytes: 0x21be3464f65effed102b3a64e941604e09bb9b73 K2 (Bob) - first 20 bytes: 0x21be3464f65effed102b3a64e941604e09bb9b73 K3 (Carol) - first 20 bytes: 0x21be3464f65effed102b3a64e941604e09bb9b73 K1 is equal to K2 K2 is equal to K3 K1 is equal to K3