Ring Signatures with GoA ring signature is a digital signature that is created by a member of a group that each have their own keys. With this it will not be possible to determine the person in the group who has created the signature. They were initially created by Ron Rivest, Adi Shamir, and Yael Tauman in 2001. We will generate a number of public keys, but only one key pair of the signer. The signer users the public keys of the others in the ring, but apply their private key, in order to sign for all the entities in the ring. No one will be able to tell which of the private keys has been used. |
Details
And so there has been a leak of information at the White House. Donald Trump calls in his Cyber Security leads, and tells them, "I know one of you leaked the information, but I can't tell which one". How can Donald tell that one of his chief leaked the information, but not know which one? Well this can be achieved with a ring signature, and which provides anonymity, unforgivably and collusion resistance.
A ring signature is a digital signature that is created by a member of a group which each have their own keys. It is then not be possible to determine the person in the group who has created the signature. The method was initially created by Ron Rivest, Adi Shamir, and Yael Tauman in 2001, and who proposed the White house leak dilemma.
In a ring signature we define a group of entities who each have public/private key pairs of (P1, S1), (P2, S2), …, (Pn, Sn). If we want entity \(i\) to sign a message (\(message\)), they use their own secret key (\(s_i\)) but the public keys of the others in the group (\(m,s_i,P_1 … P_n\)). It should then be possible to check the validity of the group by knowing the public key of the group, but not possible to determine a valid signature if there is no knowledge of the private keys within the group.
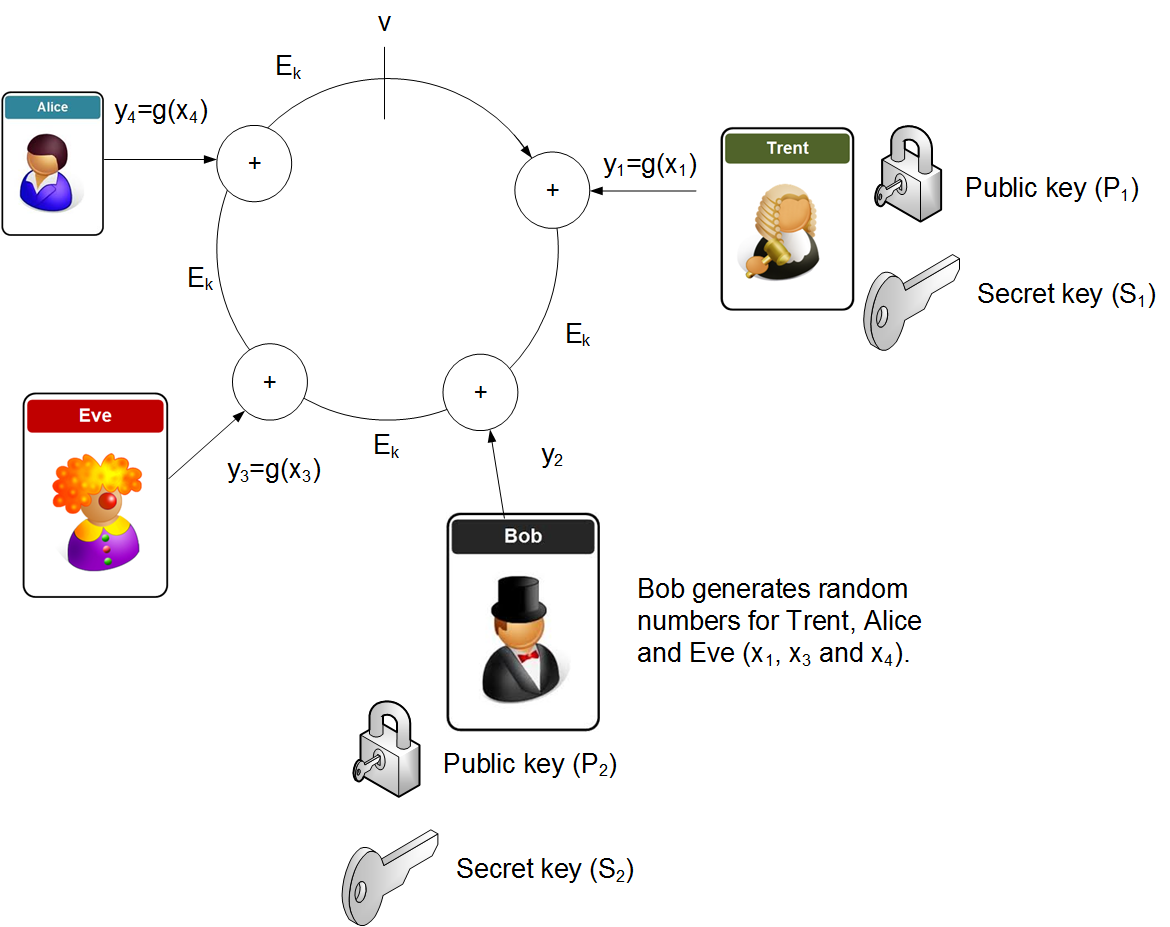
So let's say that Trent, Bob, Eve and Alice are in a group, and they each have their own public key and secret key. Bob now wants to sign a message from the group. He initially generates a random value \(v\), and then generates random values (\(s_i\)) for each of the other participants, but takes his own secret key (\(s_i\) and uses it to determine a different secret key, and which reverse of the encryption function. He next takes the message and takes a hash of it, and thus creates a key (\(k\)). This key will be used with symmetric encryption to encrypt each of the elements of the ring (\(E_k\), and each element of the ring uses an EX-OR function from the previous element (Figure 1). Each of the random values for the other participants are then encrypted with the public key of the given participant. Bob then computes the value of \(y_s\) in order to create the ring (the result of the ring must equal v). He will then inverse this value to produce the equivalent private key (xs). Bob now releases the overall signature, and the random x values, along with the computed secret key. To check the signature, the receive just computes the ring, and checks that the result matches the sent signature.
The basic method are:
1. Generate encryption with \(k=\text{Hash}(message)\).
2. Generate a random value (\(u\)).
3. Encrypt \(u\) to give \(v=E_k(u)\).
4. For each person (apart from the sender):
- 4.1 Calculate \(e=s_i^{P_i} \pmod{N_i}\) and where \(s_i\) is the random number generated for the secret key of the \(i\)th party, and \(P_i\) is the public key of the party.
- 4.2 Calculate \(v= v \oplus e\)
5. For the signed party (\(z\)), calculate \( s_z={(v \oplus u)}^d \pmod {N_z}\) and where \(d\) is the secret key of the signing party.
We will end up with the signature (\(v=E_k(u)\)), and which completes the ring.
Presentation
The following is an outline presentation [slides]:
Coding
The following defines some code [taken from here]:
package main
import (
"strconv"
"os"
"fmt"
"encoding/hex"
"go.dedis.ch/kyber/v3"
"go.dedis.ch/kyber/v3/group/edwards25519"
"go.dedis.ch/kyber/v3/sign/anon"
)
func main() {
m:="Hello"
n:=3
argCount := len(os.Args[1:])
if (argCount>0) {m= string(os.Args[1])}
if (argCount>1) {n,_= strconv.Atoi(os.Args[2])}
M := []byte(m)
suite := edwards25519.NewBlakeSHA256Ed25519()
// Create an anonymity set of random "public keys"
X := make([]kyber.Point, n)
for i := range X { // pick random points
X[i] = suite.Point().Pick(suite.RandomStream())
}
fmt.Printf("Public keys: %s\n\n",X)
// Make just one of them an actual public/private keypair (X[mine],x)
mine := 1 // only the signer knows this
x := suite.Scalar().Pick(suite.RandomStream()) // create a private key x
X[mine] = suite.Point().Mul(x, nil) // corresponding public key X
// Generate the signature
fmt.Printf("Private key of signer: %s\n\n",x)
fmt.Printf("Public key of signer: %s\n\n",X[1])
sig := anon.Sign(suite, M, anon.Set(X), nil, mine, x)
fmt.Print("Signature:\n" + hex.Dump(sig))
// Verify the signature against the correct message
tag, _ := anon.Verify(suite, M, anon.Set(X), nil, sig)
if tag == nil || len(tag) != 0 {
panic("Verify returned wrong tag")
}
fmt.Printf("\n\nSignature has been verified")
}
A sample run is:
Message: Hello Public keys: [81753b549e40804617759c9cba6878b494b8cf1d82651c504040d52acc2eb694 c45ae8f669e313183cbc7bbd6369e9423aa12c20d30da38deba7fe8da14c408a 94d45114ef11eeba37c1c9e37bd375f8f3af7b690cd7de54b9ab20e876c7e288 5dd0b5464b971d3776941a9f0df9330f1bb54423e3d12fb41b6175bc1549ba10 789c14943c31a0d56c65c75b0e0fdcc5dc7242b3a750802f1cbbcd711a3a9bce] Private key of signer: 9c7ecf02d2f0b18c470e2f0e6a0cc7b3f966b87757bab56ca3fbfdd7116ac10e Public key of signer: 01cad592c6ca5a9b397dbc15662a297a274df1f79da5dd336b9dea46a83f7399 Signature: 00000000 4c e1 3a b6 31 2d cb 79 69 91 1a 05 2a f8 46 0b |L.:.1-.yi...*.F.| 00000010 a5 b2 ea cb 5e 21 ff 23 d4 6b 03 f5 07 e4 58 0d |....^!.#.k....X.| 00000020 82 a1 49 c5 e8 f0 0a 3d 00 ec 64 e0 1a 1a 36 91 |..I....=..d...6.| 00000030 3d 5e 53 9e 81 66 b4 ba 54 cb bd c9 00 73 b3 04 |=^S..f..T....s..| 00000040 1d a0 d8 5f a3 33 78 08 cf c5 57 3f 69 f4 49 48 |..._.3x...W?i.IH| 00000050 47 aa d3 7e ae f3 d2 66 9e b0 37 80 c7 34 f5 0a |G..~...f..7..4..| 00000060 76 11 9b 2a 79 1d e0 5e 2d 21 c1 26 ec cc 18 a1 |v..*y..^-!.&....| 00000070 c0 27 f1 96 0a eb 40 d2 a3 c1 11 5e 6f 08 da 02 |.'....@....^o...| 00000080 bd 86 53 73 2c 94 b6 04 9a 05 0a 86 1f 2c d1 1e |..Ss,........,..| 00000090 ca f4 d8 60 b3 4e 36 ed 74 fd d4 32 23 06 b1 0a |...`.N6.t..2#...| 000000a0 11 b5 0b 4c f2 e0 f4 45 d9 e9 a9 3c 26 c2 78 c5 |...L...E...-&.x.| 000000b0 12 ee d7 5b 2a 65 65 c9 bf b1 31 2a eb 34 b8 04 |...[*ee...1*.4..| Signature has been verified